Single Spectrum Analysis (SSA)¶

Illustration de la méthode SSA pour les séries temporelles appliquée à la détection de points aberrants. La méthode est décrite dans Singular Spectrum Analysis: Methodology and Comparison. Voir aussi Automated outlier detection in Singular Spectrum Analysis.

Une série articielle¶

On introduit quelques points aberrants, pour le reste, elle suit le modèle $y_t = \frac{9}{10} y_{t-2} + \epsilon_t + a_t$ où $a_t$ est le bruit aberrant qui survient quelques fois.

[1]:

import numpy.random as rnd
import numpy

N = 2000
bruit1 = rnd.normal(size=(N,))
temps = numpy.arange(N)
bruit1[:5], temps[:5]

[1]:

(array([-0.24857848, -2.14896109,  0.81023497,  1.85981186, -0.04023266]),
 array([0, 1, 2, 3, 4]))

On crée un bruit aberrant.

[2]:

import random

bruit2 = numpy.zeros((N,))
for i in range(0, 10):
    h = random.randint(0, N - 1)
    bruit2[h] = rnd.normal() + 10

[3]:

serie = []
y = 10
for i in range(N // 2 + 100):
    serie.append(y + bruit1[i] + 0.0004 * temps[i] + bruit2[i])
    if i > 30:
        y = 0.9 * serie[-2]
Y = numpy.array(serie[-1000:])
Y[:5]

[3]:

array([ 0.00542873,  3.19959898, -0.04290419,  3.18763969, -1.60007673])

[4]:

import matplotlib.pyplot as plt

fig, ax = plt.subplots(1, 2, figsize=(12, 4))
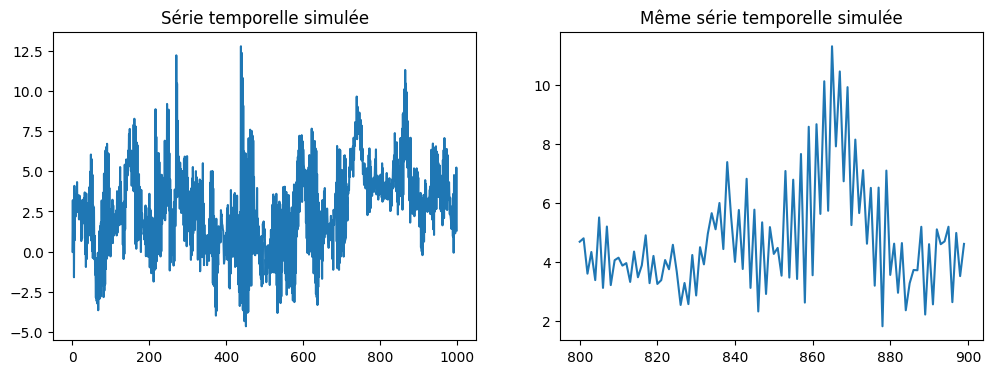
ax[0].plot(numpy.arange(len(Y)), Y)
ax[1].plot(numpy.arange(800, 900), Y[800:900])
ax[0].set_title("Série temporelle simulée")
ax[1].set_title("Même série temporelle simulée");

../../_images/practice_ml_timeseries_ssa_6_0.png

Autocorrélations¶

L’autocorrélogramme est définie par la série $cor(Y_t, Y_{t-d})_d$ . On le calcule sur la série nettoyée de sa tendance.

[5]:

from pandas import DataFrame

df = DataFrame(dict(Y=Y))
df.head()

[5]:

	Y
0	0.005429
1	3.199599
2	-0.042904
3	3.187640
4	-1.600077

[6]:

from statsmodels.tsa.tsatools import detrend

df["notrend"] = detrend(df.Y)
df.head()

[6]:

	Y	notrend
0	0.005429	-1.438347
1	3.199599	1.753363
2	-0.042904	-1.491601
3	3.187640	1.736482
4	-1.600077	-3.053695

[7]:

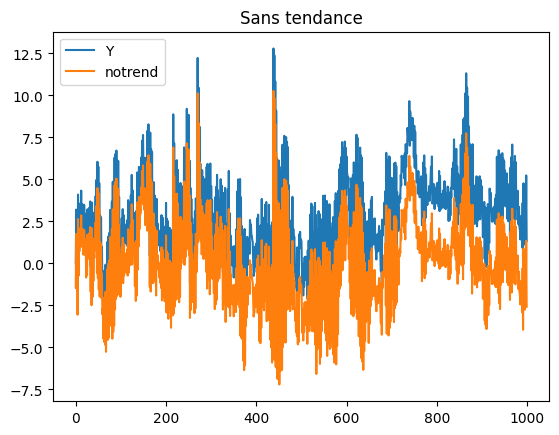
ax = df.plot()
ax.set_title("Sans tendance");

../../_images/practice_ml_timeseries_ssa_10_0.png

L’autocorrélogramme à proprement parler.

[8]:

from statsmodels.tsa.stattools import acf

cor = acf(df.notrend)
fig, ax = plt.subplots(1, 1)
ax.plot(cor)
ax.set_title("Autocorrélogramme");

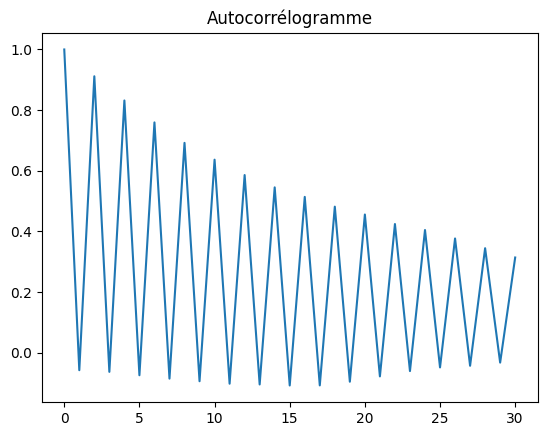
../../_images/practice_ml_timeseries_ssa_12_0.png

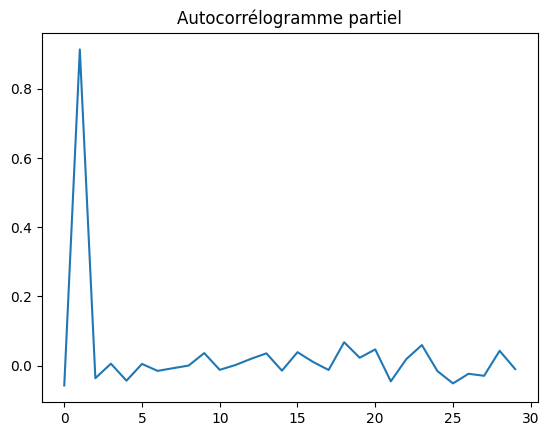
Etant donnée que la série $Y_t$ dépend de $Y_{t-2}$ , on observe un pic pour $cor(Y_t, Y_{t-2})_d$ et pour tous les $d$ pairs. $cor(Y_t, Y_{t-4}) \sim cor(Y_t, Y_{t-2})^2$ . On enlève ces effets récursifs en calculant l’autocorrélogramme partiel qui correspond à l’estimation des coefficients d’un modèle autorégressif infini.

[9]:

from statsmodels.tsa.stattools import pacf

pcor = pacf(df.notrend)
fig, ax = plt.subplots(1, 1)
ax.plot(pcor[1:])
ax.set_title("Autocorrélogramme partiel");

../../_images/practice_ml_timeseries_ssa_14_0.png

SSA¶

Ou Singular Spectrum Analysis. La méthode part de la matrice des séries décalées qu’on décompose avec la méthode SVD ou Singular Value Decomposition.

[10]:

def lagged_ts(serie, lag):
    dim = serie.shape[0]
    res = numpy.zeros((dim - lag + 1, lag))
    for i in range(lag):
        res[:, i] = serie[i : dim - lag + i + 1]
    return res


lagged_ts(Y, 3)

[10]:

array([[ 0.00542873,  3.19959898, -0.04290419],
       [ 3.19959898, -0.04290419,  3.18763969],
       [-0.04290419,  3.18763969, -1.60007673],
       ...,
       [ 1.13700254,  4.06081016,  1.89449208],
       [ 4.06081016,  1.89449208,  5.23733857],
       [ 1.89449208,  5.23733857,  1.32045675]])

[11]:

lag = lagged_ts(Y, 60)
lag.shape

[11]:

(941, 60)

[12]:

from numpy.linalg import svd

# u @ numpy.diag(s) @ vh
u, s, vh = svd(lag)

[13]:

u.shape, s.shape, vh.shape

[13]:

((941, 941), (60,), (60, 60))

[14]:

d = numpy.zeros((941, 60))
d[:60, :60] = numpy.diag(s)

[15]:

(u @ d @ vh).shape

[15]:

(941, 60)

[16]:

fig, ax = plt.subplots(1, 2, figsize=(12, 4))
DataFrame(dict(valeur=s)).plot(kind="bar", ax=ax[0])
DataFrame(dict(valeur=s[1:15])).plot(kind="bar", ax=ax[1])
ax[0].set_title("Valeurs propres")
ax[1].set_title("Valeurs propres sans la première");

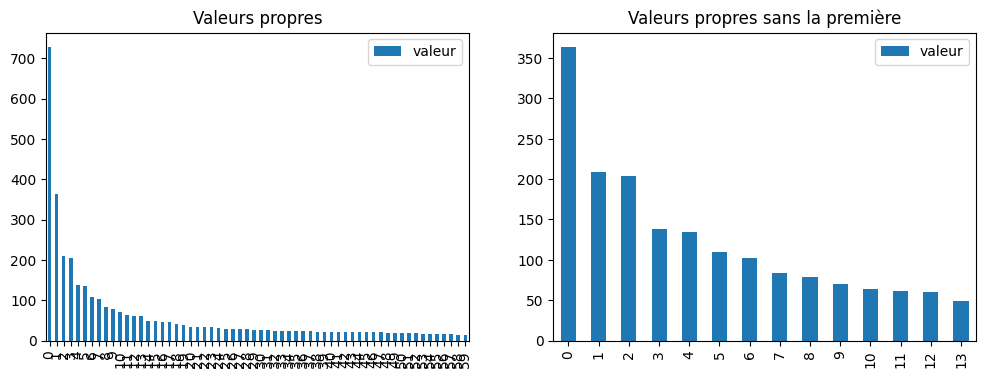
../../_images/practice_ml_timeseries_ssa_22_0.png

Je me représente la méthode SVD comme une façon de projeter des vecteurs sur l’espace vectoriel constitué des premiers vecteurs propres, à chaque dimension supplémentaire, c’est comme une pièce du puzzle qui s’assemble jusqu’à recomposer l’ensemble. Ce qu’on peut voir aussi comme ceci :

[17]:

np = 12
fig, ax = plt.subplots(np, 3, figsize=(14, np * 2))
for n in range(np):
    i = n if n < 5 else n * 5 - 15
    d = numpy.zeros((941, 60))
    d[i, i] = s[i]
    X2 = u @ d @ vh
    pos = 0  # X2.shape[1] - 1

    # série reconstruites avec un axe
    ax[n, 0].plot(X2[:, pos])
    ax[n, 1].set_title("i=%d" % i)
    # série reconstruites avec un axe
    ax[n, 1].plot(X2[800:850, pos])
    ax[n, 1].set_title("i=%d" % i)

    d = numpy.zeros((941, 60))
    d[: i + 1, : i + 1] = numpy.diag(s[: i + 1])
    X2 = u @ d @ vh
    ax[n, 2].plot(X2[800:850, pos])
    ax[n, 2].plot(Y[800:850])
    ax[n, 2].set_title("-->i=%d + 1" % i)

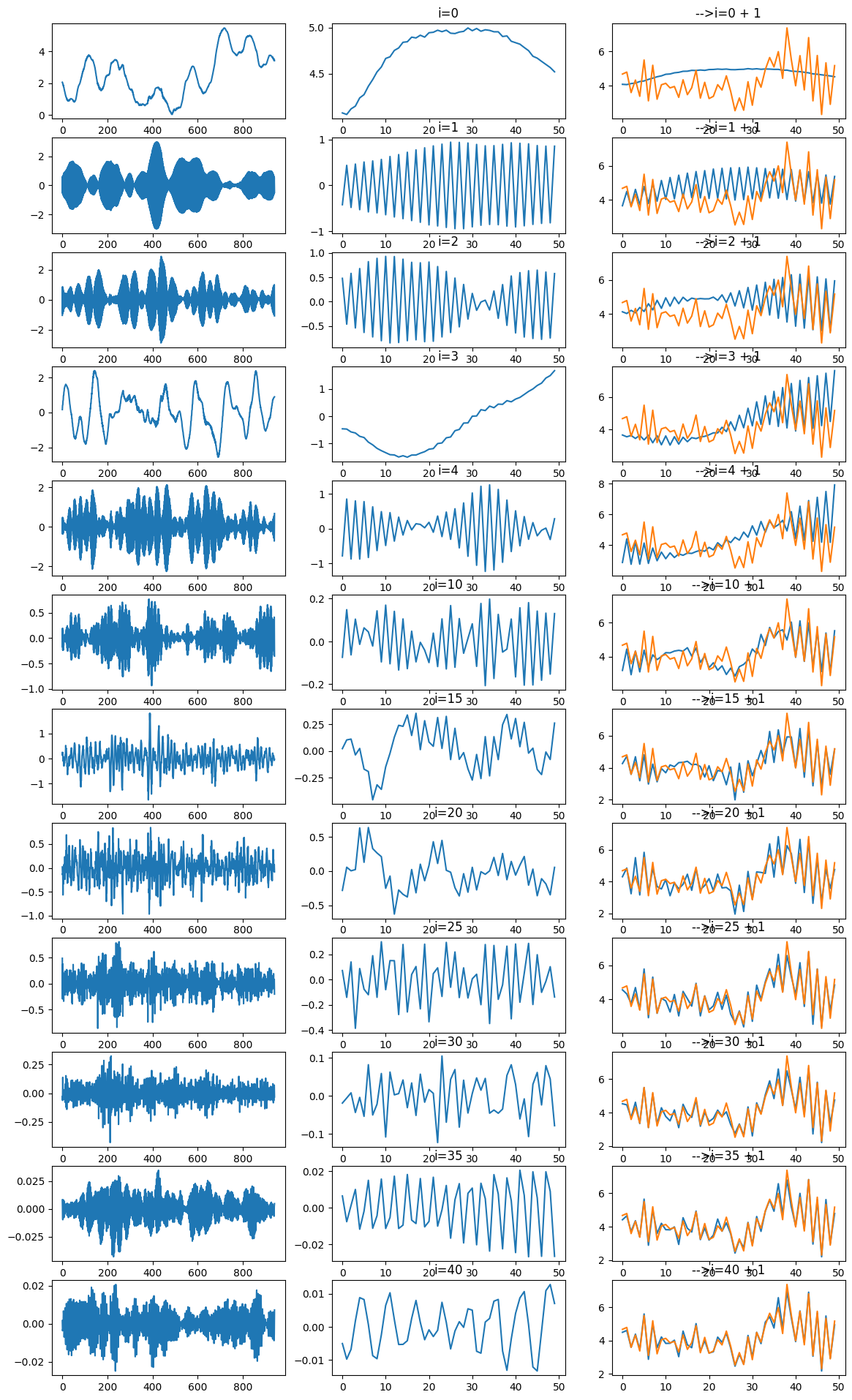
../../_images/practice_ml_timeseries_ssa_24_0.png

La prédiction¶

On veut prédire $Y_{t+1}$ . L’idée consiste à appliquer la méthode en considérent $Y_{t+1}$ égale à $Y_t$ puis à remplacer cette prédiction par la valeur de la série reconstruite. On peut même prédire à un horizon plus grand que la valeur suivante.

[18]:

fig, ax = plt.subplots(1, 1, figsize=(5, 5))
for i in range(0, 8):
    ax.plot([0, 5], [i, i], "k-")
    if i < 6:
        ax.plot([i, i], [0, 7], "k-")
    if i < 4:
        ax.text(i + 0.1, 1.5, "Y(t-%d)" % (4 - i))
        ax.text(i + 0.1, 0.5, "Y(t-%d)" % (3 - i))
ax.text(4.1, 1.5, "Y(t)")
ax.text(4.05, 0.5, "Y(t+1)=?")
plt.axis("off");

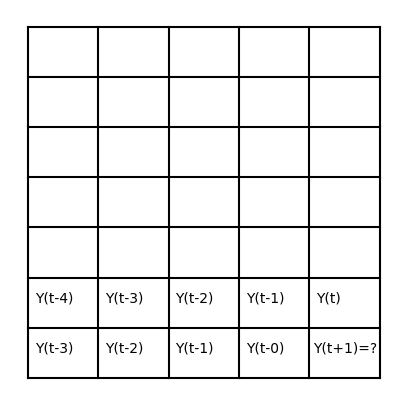
../../_images/practice_ml_timeseries_ssa_26_0.png

Les points aberrants¶

On repère les points aberrants avec l’une méthode de son choix sur la série reconstruite.

[19]:

d = numpy.zeros((941, 60))
for i in range(0, 30):
    d[i, i] = s[i]
X2 = u @ d @ vh

[23]:

from sklearn.covariance import EllipticEnvelope

env = EllipticEnvelope(support_fraction=0.9)
env.fit(X2[:, :30])

[23]:

EllipticEnvelope(support_fraction=0.9)

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

L’idéal serait d’utiliser une méthode basée sur une ACP. Le plus proche reste le modèle gaussien avec EllipticEnvelope.

[24]:

out = env.predict(X2[:, :30])

fig, ax = plt.subplots(1, 1, figsize=(12, 2))
ax.plot((1 - out) / 2, "-")
ax.set_title("Points aberrants d'une série temporelles.");

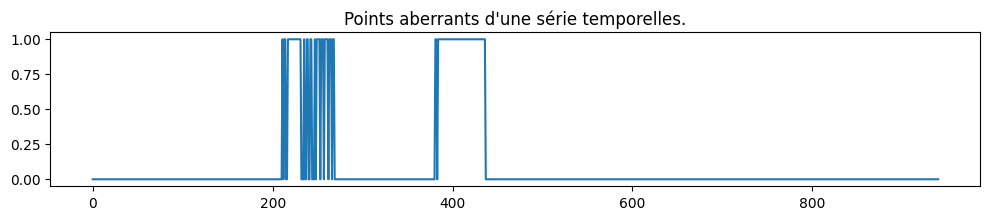
../../_images/practice_ml_timeseries_ssa_31_0.png

On observe des plages contiguës. Cela signifie que d’une valeur aberrante contamine des vecteurs décalées consécutifs de la série $Y$ . Il ne reste plus qu’à repérer la valeur incriminée.

[25]:

fig, ax = plt.subplots(1, 1, figsize=(14, 2))
ax.plot(X2[:, 0], label="serie")
ax.plot((1 - out) * 5, "-", label="outlier")
ax.set_title("Points aberrants sur la série reconstruite")
ax.legend();

../../_images/practice_ml_timeseries_ssa_33_0.png

[26]:

fig, ax = plt.subplots(1, 1, figsize=(14, 2))
ax.plot(Y, label="serie")
ax.plot((1 - out) * 5, "-", label="outlier")
ax.set_title("Points aberrants sur la série brute")
ax.legend();

../../_images/practice_ml_timeseries_ssa_34_0.png

Ce qui a l’air de correspondre à la fin des grandes plages. On recommence avec la probabilité d’être un outlier.

[27]:

fig, ax = plt.subplots(1, 1, figsize=(14, 2))
outp = env.decision_function(X2[:, :30])
ax.plot(Y, label="serie")
ax.plot(outp, "-", label="Proba not outlier")
ax.set_title("Points aberrants sur la série brute")
ax.legend();

../../_images/practice_ml_timeseries_ssa_36_0.png

Notebook on github