Classification multi-classe et jeu mal balancé¶

Plus il y a de classes, plus la classification est difficile car le nombre d’exemples par classe diminue. Voyons cela plus en détail sur des jeux artificiels produits mar make_blobs.

[1]:

%matplotlib inline

Pour aller plus vite, l’apprentissage est un peu écourté. Le code produit beaucoup de warnings indiquant que la convergence n’a pas eu lieu et nécessite plus d’itérations. Cela ne remet pas en cause ce qui est illustré dans ce notebook.

[2]:

import warnings

warnings.filterwarnings("ignore")

découverte¶

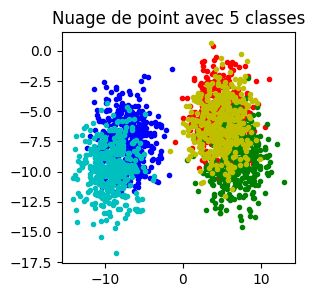
Le premier jeu de données est une simple fonction linéaire sur deux variables d’ordre de grandeur différents.

[3]:

from sklearn.datasets import make_blobs
from sklearn.model_selection import train_test_split

X, y = make_blobs(2000, cluster_std=2, centers=5)

[4]:

import matplotlib.pyplot as plt

fig, ax = plt.subplots(1, 1, figsize=(3, 3))
for i, c in zip(range(0, 5), "rgbyc"):
    ax.plot(X[y == i, 0], X[y == i, 1], c + ".", label=str(i))
ax.set_title("Nuage de point avec 5 classes")

[4]:

Text(0.5, 1.0, 'Nuage de point avec 5 classes')

../../_images/practice_ml_artificiel_multiclass_7_1.png

[5]:

X_train, X_test, y_train, y_test = train_test_split(X, y)

[6]:

from sklearn.linear_model import LogisticRegression

model = LogisticRegression(solver="sag")
model.fit(X_train, y_train)
score = model.score(X_test, y_test)
score

[6]:

0.658

Mettons le jour dans une fonction pour plusieurs modèles :

[7]:

from time import perf_counter as clock


def evaluate_model(models, X_train, X_test, y_train, y_test):
    res = {}
    for k, v in models.items():
        t1 = clock()
        v.fit(X_train, y_train)
        t2 = clock() - t1
        res[k + "_time_train"] = t2
        t1 = clock()
        score = v.score(X_test, y_test)
        t2 = clock() - t1
        res[k + "_time_test"] = t2
        res[k + "_score"] = score
    return res


from sklearn.multiclass import OneVsOneClassifier, OneVsRestClassifier

models = {
    "OvO-LR": OneVsOneClassifier(LogisticRegression(solver="sag")),
    "OvR-LR": OneVsRestClassifier(LogisticRegression(solver="sag")),
    "LR": LogisticRegression(),
}

res = evaluate_model(models, X_train, X_test, y_train, y_test)
res

[7]:

{'OvO-LR_time_train': 0.2209448000003249,
 'OvO-LR_time_test': 0.009104000000206725,
 'OvO-LR_score': 0.662,
 'OvR-LR_time_train': 0.2086589999998978,
 'OvR-LR_time_test': 0.005245500000000902,
 'OvR-LR_score': 0.654,
 'LR_time_train': 0.05842000000029657,
 'LR_time_test': 0.0010207000000264088,
 'LR_score': 0.66}

La stratégie OneVsOne a l’air d’être plus performante. La régression logistique implémente la stratégie OneVsRest. On ne l’évalue plus.

[8]:

import pandas
from tqdm import tqdm

warnings.filterwarnings("ignore")

models = {
    "OvO-LR": OneVsOneClassifier(LogisticRegression(solver="sag")),
    "OvR-LR": LogisticRegression(solver="sag"),
}

rows = []
for centers in tqdm(range(2, 51, 8)):
    X, y = make_blobs(500, centers=centers, cluster_std=2.0)
    X_train, X_test, y_train, y_test = train_test_split(X, y)
    res = evaluate_model(models, X_train, X_test, y_train, y_test)
    res["centers"] = centers
    rows.append(res)

df = pandas.DataFrame(rows)
df

100%|██████████| 7/7 [00:10<00:00,  1.56s/it]

[8]:

	OvO-LR_time_train	OvO-LR_time_test	OvO-LR_score	OvR-LR_time_train	OvR-LR_time_test	OvR-LR_score	centers
0	0.032755	0.001730	1.000	0.022686	0.001637	1.000	2
1	0.324123	0.032629	0.812	0.076139	0.001591	0.808	10
2	0.730089	0.036648	0.488	0.053406	0.000859	0.508	18
3	0.984762	0.096167	0.444	0.116836	0.001022	0.468	26
4	1.537234	0.154609	0.384	0.110220	0.001036	0.388	34
5	2.595010	0.209428	0.328	0.122475	0.000956	0.336	42
6	3.022290	0.437165	0.280	0.150593	0.000868	0.280	50

[9]:

fix, ax = plt.subplots(1, 1, figsize=(6, 3))
for c, col in zip("rgb", [_ for _ in df.columns if "_score" in _]):
    df.plot(x="centers", y=col, label=col.replace("_score", ""), ax=ax, color=c)
x = list(range(2, 51))
ax.plot(x, [1.0 / _ for _ in x], label="constante")
ax.legend()
ax.set_title("Précision en fonction du nombre de classes");

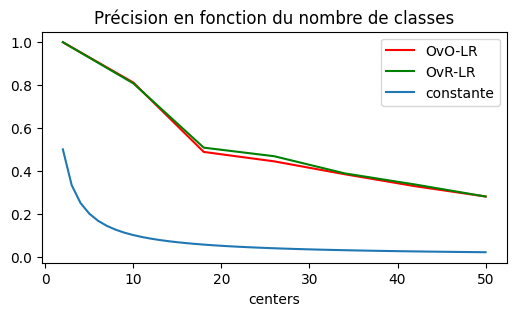
../../_images/practice_ml_artificiel_multiclass_14_0.png

évolution en fonction du nombre de classes¶

On pourrait se dire que c’est parce que le nombre d’exemples par classes décroît. Voyons cela.

[10]:

import pandas

models = {
    "OvO-LR": OneVsOneClassifier(LogisticRegression(solver="sag")),
    "OvR-LR": OneVsRestClassifier(LogisticRegression(solver="sag")),
}

rows = []
for centers in tqdm(range(2, 51, 8)):
    X, y = make_blobs(50 * centers, centers=centers, cluster_std=2.0)
    X_train, X_test, y_train, y_test = train_test_split(X, y)
    res = evaluate_model(models, X_train, X_test, y_train, y_test)
    res["centers"] = centers
    rows.append(res)

df2 = pandas.DataFrame(rows)
df2

100%|██████████| 7/7 [00:23<00:00,  3.30s/it]

[10]:

	OvO-LR_time_train	OvO-LR_time_test	OvO-LR_score	OvR-LR_time_train	OvR-LR_time_test	OvR-LR_score	centers
0	0.009756	0.003354	0.980000	0.016191	0.001600	0.980000	2
1	0.248614	0.011291	0.636000	0.092591	0.001695	0.568000	10
2	0.834381	0.067650	0.524444	0.376624	0.004853	0.466667	18
3	1.502573	0.099040	0.460000	0.721085	0.004124	0.436923	26
4	2.613464	0.178248	0.397647	0.990700	0.005284	0.342353	34
5	4.057976	0.297401	0.375238	1.337764	0.006087	0.340952	42
6	6.861960	0.479451	0.316800	2.269823	0.008297	0.269600	50

[11]:

fix, ax = plt.subplots(1, 1, figsize=(8, 4))
for c1, c2, col in zip("rg", "cy", [_ for _ in df2.columns if "_score" in _]):
    df.plot(
        x="centers", y=col, label=col.replace("_score", " N const"), ax=ax, color=c1
    )
    df2.plot(
        x="centers", y=col, label=col.replace("_score", " cl const"), ax=ax, color=c2
    )
x = list(range(2, 51))
ax.plot(x, [1.0 / _ for _ in x], label="constante")
ax.legend()
ax.set_title("Précision en fonction du nombre de classes");

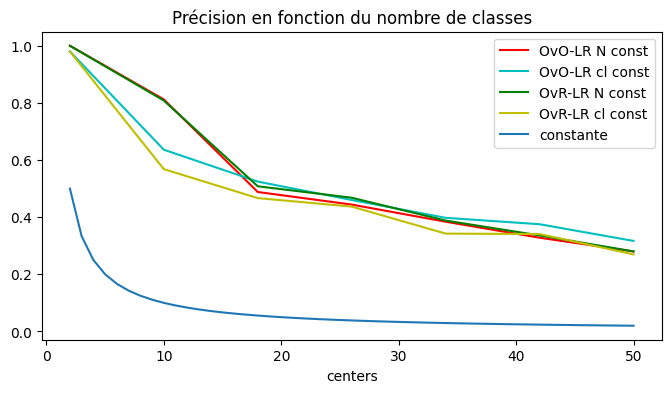
../../_images/practice_ml_artificiel_multiclass_18_0.png

évolution en fonction de la variance¶

Un peu mieux mais cela décroît toujours. Peut-être que la courbe dépend de la confusion entre les classes ?

[12]:

import pandas

models = {
    "OvO-LR": OneVsOneClassifier(LogisticRegression(solver="sag")),
    "OvR-LR": OneVsRestClassifier(LogisticRegression(solver="sag")),
}

rows = []
for std_ in tqdm(range(5, 31, 5)):
    X, y = make_blobs(500, centers=40, cluster_std=std_ / 10.0)
    X_train, X_test, y_train, y_test = train_test_split(X, y)
    res = evaluate_model(models, X_train, X_test, y_train, y_test)
    res["std"] = std_ / 10.0
    rows.append(res)

df3 = pandas.DataFrame(rows)
df3

100%|██████████| 6/6 [00:16<00:00,  2.78s/it]

[12]:

	OvO-LR_time_train	OvO-LR_time_test	OvO-LR_score	OvR-LR_time_train	OvR-LR_time_test	OvR-LR_score	std
0	2.031314	0.243204	0.788	0.584626	0.005322	0.560	0.5
1	1.901009	0.275102	0.600	0.527490	0.008637	0.420	1.0
2	1.790364	0.245218	0.496	0.538992	0.005838	0.372	1.5
3	1.985556	0.258749	0.280	0.459469	0.005051	0.228	2.0
4	2.154060	0.258028	0.220	0.603545	0.005316	0.192	2.5
5	2.031245	0.208715	0.200	0.529591	0.005976	0.180	3.0

[13]:

fix, ax = plt.subplots(1, 1, figsize=(8, 4))
for c1, col in zip("rg", [_ for _ in df3.columns if "_score" in _]):
    df3.plot(x="std", y=col, label=col.replace("_score", " cl const"), ax=ax, color=c1)
x = [_ / 10.0 for _ in range(5, 31)]
ax.plot(x, [1 / 40.0 for _ in x], label="constante")
ax.set_title("Précision en fonction de la variance de chaque classe")
ax.legend();

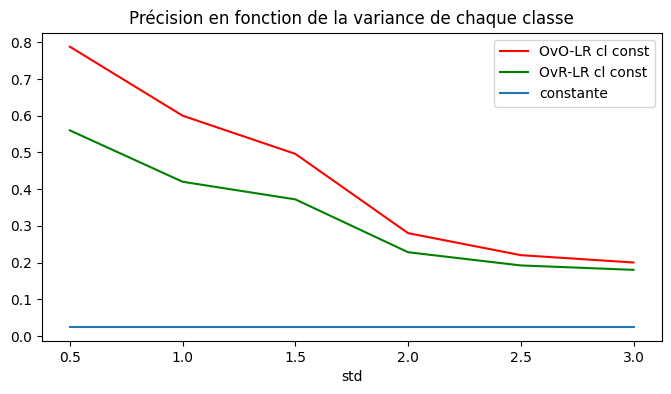
../../_images/practice_ml_artificiel_multiclass_22_0.png

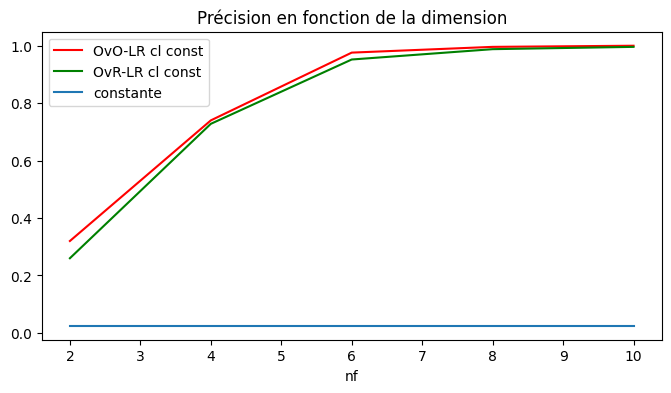
évolution en fonction de la dimension¶

Et en fonction du nombre de dimensions :

[14]:

import pandas

models = {
    "OvO-LR": OneVsOneClassifier(LogisticRegression(solver="sag")),
    "OvR-LR": OneVsRestClassifier(LogisticRegression(solver="sag")),
}

rows = []
for nf in tqdm(range(2, 11, 2)):
    X, y = make_blobs(500, centers=40, cluster_std=2.0, n_features=nf)
    X_train, X_test, y_train, y_test = train_test_split(X, y)
    res = evaluate_model(models, X_train, X_test, y_train, y_test)
    res["nf"] = nf
    rows.append(res)

df4 = pandas.DataFrame(rows)
df4

100%|██████████| 5/5 [00:17<00:00,  3.56s/it]

[14]:

	OvO-LR_time_train	OvO-LR_time_test	OvO-LR_score	OvR-LR_time_train	OvR-LR_time_test	OvR-LR_score	nf
0	2.042428	0.264521	0.320	0.491270	0.005313	0.260	2
1	2.325670	0.225577	0.740	0.760807	0.005378	0.728	4
2	2.953030	0.214104	0.976	0.865434	0.005122	0.952	6
3	2.404396	0.234881	0.996	0.967371	0.009054	0.988	8
4	2.818875	0.287795	1.000	0.898213	0.005280	0.996	10

[15]:

fix, ax = plt.subplots(1, 1, figsize=(8, 4))
for c1, col in zip("rg", [_ for _ in df4.columns if "_score" in _]):
    df4.plot(x="nf", y=col, label=col.replace("_score", " cl const"), ax=ax, color=c1)
x = list(range(2, 11))
ax.plot(x, [1 / 40.0 for _ in x], label="constante")
ax.set_title("Précision en fonction de la dimension")
ax.legend();

../../_images/practice_ml_artificiel_multiclass_26_0.png

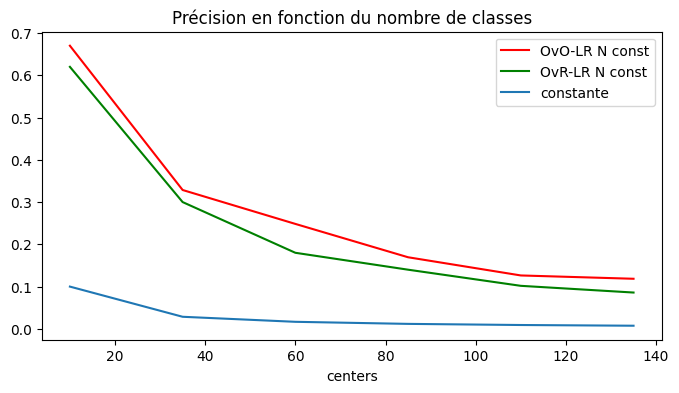
retour sur le nombre de classes¶

[22]:

import pandas

models = {
    "OvO-LR": OneVsOneClassifier(LogisticRegression(solver="lbfgs")),
    "OvR-LR": OneVsRestClassifier(LogisticRegression(solver="lbfgs")),
}

rows = []
for centers in tqdm(range(10, 151, 25)):
    X, y = make_blobs(10 * centers, centers=centers, cluster_std=2.0)
    X_train, X_test, y_train, y_test = train_test_split(X, y)
    res = evaluate_model(models, X_train, X_test, y_train, y_test)
    res["centers"] = centers
    rows.append(res)

df5 = pandas.DataFrame(rows)
df5

100%|██████████| 6/6 [01:45<00:00, 17.58s/it]

[22]:

	OvO-LR_time_train	OvO-LR_time_test	OvO-LR_score	OvR-LR_time_train	OvR-LR_time_test	OvR-LR_score	centers
0	0.285135	0.017950	0.600000	0.042483	0.002003	0.520000	10
1	2.895627	0.189201	0.302857	0.168547	0.004620	0.251429	35
2	7.890931	0.605583	0.196667	0.367130	0.013213	0.160000	60
3	17.404424	1.189003	0.160000	0.499927	0.012866	0.105882	85
4	26.166851	1.902685	0.132727	0.772086	0.014063	0.083636	110
5	41.347375	2.720673	0.120000	0.901161	0.043177	0.084444	135

[17]:

fix, ax = plt.subplots(1, 1, figsize=(8, 4))
for c1, col in zip("rgcy", [_ for _ in df5.columns if "_score" in _]):
    df5.plot(
        x="centers", y=col, label=col.replace("_score", " N const"), ax=ax, color=c1
    )
x = df5.centers
ax.plot(x, [1.0 / _ for _ in x], label="constante")
ax.legend()
ax.set_title("Précision en fonction du nombre de classes");

../../_images/practice_ml_artificiel_multiclass_29_0.png

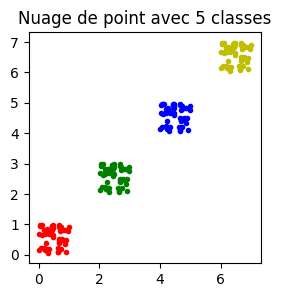
un dernier jeu sûr¶

On construit un dernier jeu pour lequel le taux de classification devrait être 100%.

[18]:

import numpy


def jeu_x_y(ncl, n):
    uni = numpy.random.random(n * 2).reshape((n, 2))
    resx = []
    resy = []
    for i in range(ncl):
        resx.append(uni + i * 2)
        resy.append(numpy.ones(n) * i)
    X = numpy.vstack(resx)
    y = numpy.hstack(resy)
    return X, y


X, y = jeu_x_y(4, 50)
X.shape, y.shape

[18]:

((200, 2), (200,))

[19]:

fig, ax = plt.subplots(1, 1, figsize=(3, 3))
for i, c in zip(range(0, 5), "rgbyc"):
    ax.plot(X[y == i, 0], X[y == i, 1], c + ".", label=str(i))
ax.set_title("Nuage de point avec 5 classes")

[19]:

Text(0.5, 1.0, 'Nuage de point avec 5 classes')

../../_images/practice_ml_artificiel_multiclass_32_1.png

[20]:

from sklearn.tree import DecisionTreeClassifier

models = {
    "OvO-LR": OneVsOneClassifier(LogisticRegression(solver="sag")),
    "OvR-LR": OneVsRestClassifier(LogisticRegression(solver="sag")),
    "DT": DecisionTreeClassifier(),
}

rows = []
for centers in tqdm(range(2, 21, 4)):
    X, y = jeu_x_y(centers, 10)
    X_train, X_test, y_train, y_test = train_test_split(X, y)
    res = evaluate_model(models, X_train, X_test, y_train, y_test)
    res["centers"] = centers
    rows.append(res)

df5 = pandas.DataFrame(rows)
df5

100%|██████████| 5/5 [00:00<00:00,  5.22it/s]

[20]:

	OvO-LR_time_train	OvO-LR_time_test	OvO-LR_score	OvR-LR_time_train	OvR-LR_time_test	OvR-LR_score	DT_time_train	DT_time_test	DT_score	centers
0	0.008709	0.003290	1.000000	0.014272	0.002550	1.000000	0.001384	0.001313	1.0	2
1	0.050579	0.007302	0.800000	0.025281	0.002580	0.733333	0.001434	0.001112	1.0	6
2	0.100356	0.013768	0.400000	0.032940	0.001779	0.320000	0.001064	0.000719	1.0	10
3	0.185524	0.020908	0.285714	0.046669	0.001958	0.085714	0.001124	0.000627	1.0	14
4	0.292794	0.039437	0.311111	0.083591	0.003007	0.111111	0.001478	0.000881	1.0	18

[21]:

fix, ax = plt.subplots(1, 1, figsize=(8, 4))
for c1, col in zip("rgycbp", [_ for _ in df5.columns if "_score" in _]):
    df5.plot(
        x="centers", y=col, label=col.replace("_score", " N const"), ax=ax, color=c1
    )
x = df5.centers
ax.plot(x, [1.0 / _ for _ in x], label="constante")
ax.legend()
ax.set_title("Précision en fonction du nombre de classes\njeu simple");

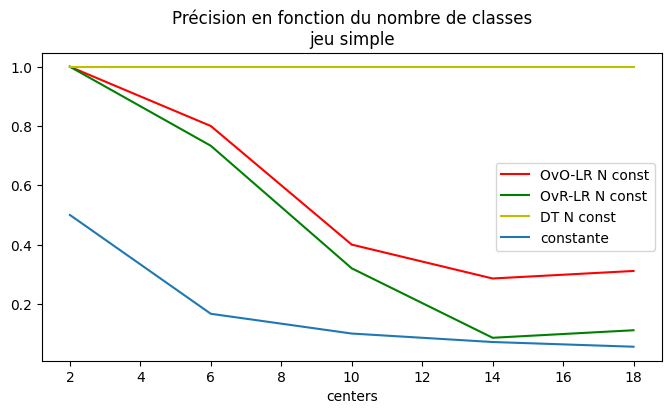
../../_images/practice_ml_artificiel_multiclass_34_0.png

La régression logistique n’est pas le meilleur modèle lorsque le nombre de classes est élevé et la dimension de l’espace de variables faible.

Notebook on github