Receiver Operating Characteristic (ROC)

Un problème de classification binaire consiste à trouver un moyen de séparer deux nuages de points (voir classification) et on évalue le plus souvent sa pertinence à l’aide d’une courbe ROC. Cet exemple montre différente représentation de la même information.

Classification binaire

On commence par générer un nuage de points artificiel.

import numpy
from sklearn.metrics import (
    f1_score,
    precision_recall_curve,
    roc_curve,
    confusion_matrix,
)
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.datasets import make_classification
import matplotlib.pyplot as plt
from teachpyx.ext_test_case import unit_test_going

X, Y = make_classification(
    n_samples=10000 if unit_test_going() else 100,
    n_features=2,
    n_classes=2,
    n_repeated=0,
    n_redundant=0,
)

On représente ces données.

fig = plt.figure(figsize=(5, 5))
ax = plt.subplot()
ax.plot(X[Y == 0, 0], X[Y == 0, 1], ".b")
ax.plot(X[Y == 1, 0], X[Y == 1, 1], ".r")

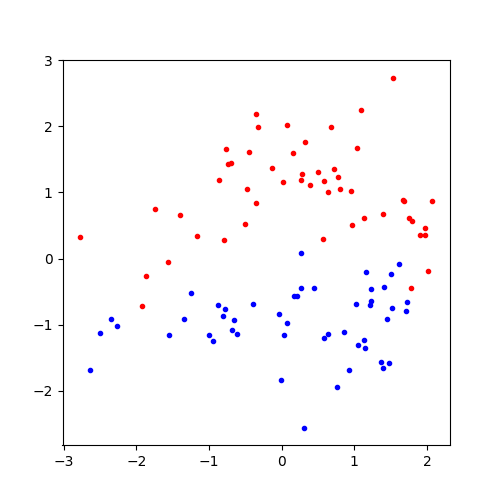
[<matplotlib.lines.Line2D object at 0x7f1658341750>]

On découpe en train / test.

X_train, X_test, y_train, y_test = train_test_split(X, Y)

On apprend sur la base d’apprentissage.

logreg = LogisticRegression()
logreg.fit(X_train, y_train)

LogisticRegression()

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

Et on prédit sur la base de test.

y_pred = logreg.predict(X_test)

On calcule la matrice de confusion.

conf = confusion_matrix(y_test, y_pred)
print(conf)

[[12  0]
 [ 3 10]]

Trois courbes

La courbe ROC s’applique toujours à un problème de classification binaire qu’on peut scinder en trois questions :

• Le modèle a bien classé un exemple dans la classe 0.

• Le modèle a bien classé un exemple dans la classe 1.

• Le modèle a bien classé un exemple, que ce soit dans la classe 0 ou la classe 1. Ce problème suppose implicitement que le même seuil est utilisé sur chacun des classes. C’est-à-dire qu’on prédit la classe 1 si le score pour la classe 1 est supérieur à à celui obtenu pour la classe 0 mais aussi qu’on valide la réponse si le score de la classe 1 ou celui de la classe 0 est supérieur au même seuil s, ce qui n’est pas nécessairement le meilleur choix.

Si les réponses sont liées, le modèle peut répondre de manière plus ou moins efficace à ces trois questions. On calcule les courbes ROC à ces trois questions.

fpr_cl = dict()
tpr_cl = dict()

y_pred = logreg.predict(X_test)
y_proba = logreg.predict_proba(X_test)

fpr_cl["classe 0"], tpr_cl["classe 0"], _ = roc_curve(
    y_test == 0, y_proba[:, 0].ravel()
)
fpr_cl["classe 1"], tpr_cl["classe 1"], _ = roc_curve(
    y_test, y_proba[:, 1].ravel()
)  # y_test == 1

prob_pred = numpy.array([y_proba[i, 1 if c else 0] for i, c in enumerate(y_pred)])
fpr_cl["tout"], tpr_cl["tout"], _ = roc_curve((y_pred == y_test).ravel(), prob_pred)

Et on les représente.

plt.figure()
for key in fpr_cl:
    plt.plot(fpr_cl[key], tpr_cl[key], label=key)

lw = 2
plt.plot([0, 1], [0, 1], color="navy", lw=lw, linestyle="--")
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel("Proportion mal classée")
plt.ylabel("Proportion bien classée")
plt.title("ROC(s) avec predict_proba")
plt.legend(loc="lower right")

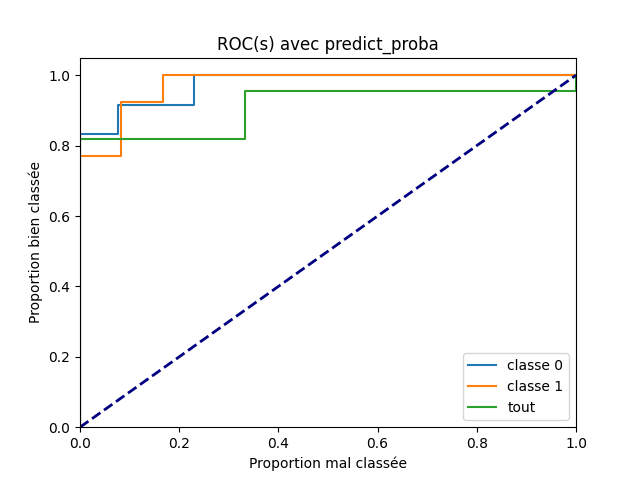
<matplotlib.legend.Legend object at 0x7f16578bab00>

predict_proba ou decision_function

Le fait que la courbe ROC pour la dernière question, les deux classes à la fois, suggère que les seuils optimaux seront différents pour les deux premières questions. La courbe ROC ne change pas qu’on prenne la fonction predict_proba ou decision_function car ces deux scores sont liés par une fonction monotone. On recommence avec la seconde fonction.

y_pred = logreg.predict(X_test)
y_proba = logreg.decision_function(X_test)
y_proba = numpy.vstack([-y_proba, y_proba]).T

fpr_cl["classe 0"], tpr_cl["classe 0"], _ = roc_curve(
    y_test == 0, y_proba[:, 0].ravel()
)
fpr_cl["classe 1"], tpr_cl["classe 1"], _ = roc_curve(
    y_test, y_proba[:, 1].ravel()
)  # y_test == 1
prob_pred = numpy.array([y_proba[i, 1 if c else 0] for i, c in enumerate(y_pred)])
fpr_cl["tout"], tpr_cl["tout"], _ = roc_curve((y_pred == y_test).ravel(), prob_pred)

plt.figure()
for key in fpr_cl:
    plt.plot(fpr_cl[key], tpr_cl[key], label=key)

lw = 2
plt.plot([0, 1], [0, 1], color="navy", lw=lw, linestyle="--")
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel("Proportion mal classée")
plt.ylabel("Proportion bien classée")
plt.title("ROC(s) avec decision_function")
plt.legend(loc="lower right")

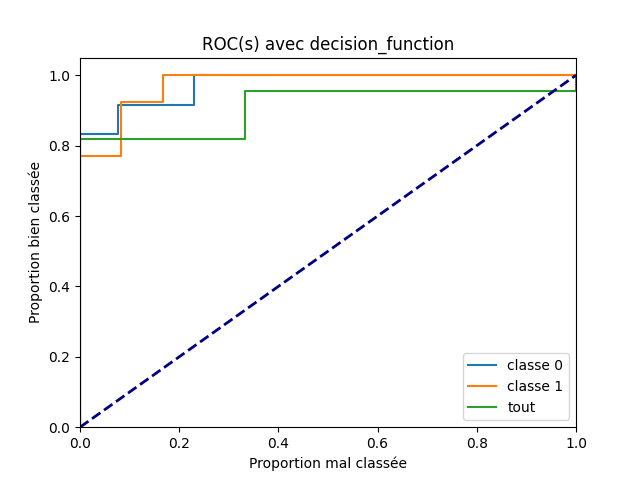
<matplotlib.legend.Legend object at 0x7f16586430d0>

Precision Rappel

En ce qui me concerne, je n’arrive jamais à retenir la définition de False Positive Rate (FPR) and True Positive Rate (TPR). Je lui préfère la précision et le rappel. Pour un seuil donné, le rappel est l’ensemble de ces documents dont le score est supérieur à un seuil s, la précision est l’ensemble des documents bien classé parmi ceux-ci. On utilise la fonction precision_recall_curve.

y_pred = logreg.predict(X_test)
y_proba = logreg.predict_proba(X_test)


prec = dict()
rapp = dict()

prec["classe 0"], rapp["classe 0"], _ = precision_recall_curve(
    y_test == 0, y_proba[:, 0].ravel()
)
prec["classe 1"], rapp["classe 1"], _ = precision_recall_curve(
    y_test, y_proba[:, 1].ravel()
)  # y_test == 1
prob_pred = numpy.array([y_proba[i, 1 if c else 0] for i, c in enumerate(y_pred)])
prec["tout"], rapp["tout"], _ = precision_recall_curve(
    (y_pred == y_test).ravel(), prob_pred
)

plt.figure()
for key in fpr_cl:
    plt.plot(prec[key], rapp[key], label=key)

plt.plot([0, 1], [0, 1], color="navy", lw=2, linestyle="--")
plt.xlabel("Précision")
plt.ylabel("Rappel")
plt.title("Courbe Précision / Rappel")
plt.legend(loc="lower right")

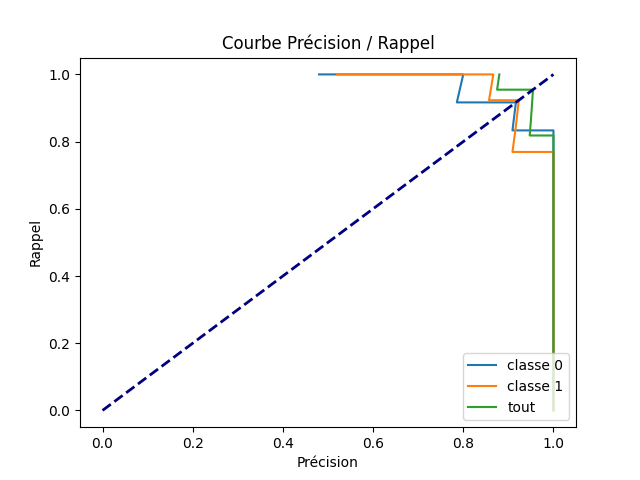
<matplotlib.legend.Legend object at 0x7f1657df0220>

Métrique F1

La courbe Précision / Rappel ne montre pas les scores même s’il intervient dans chaque point de la courbe. Pour le faire apparaître, on utilise un graphe où il est en abscisse. La métrique F1 propose une pondération entre les deux : .

y_pred = logreg.predict(X_test)
y_proba = logreg.predict_proba(X_test)
prec, rapp, seuil = precision_recall_curve(y_test == 1, y_proba[:, 1].ravel())
f1 = [
    f1_score(y_test[y_proba[:, 1] >= s].ravel(), y_pred[y_proba[:, 1] >= s])
    for s in seuil.ravel()
]

y_score = logreg.decision_function(X_test)
precd, rappd, seuild = precision_recall_curve(y_test == 1, y_score.ravel())
f1d = [
    f1_score(y_test[y_score >= s].ravel(), y_pred[y_score >= s]) for s in seuil.ravel()
]

fig, ax = plt.subplots(1, 2, figsize=(12, 4))
ax[0].plot(seuil, prec[1:], label="Précision")
ax[0].plot(seuil, rapp[1:], label="Rappel")
ax[0].plot(seuil, f1, label="F1")
ax[0].set_title("predict_proba")
ax[0].legend()

ax[1].plot(seuild, precd[1:], label="Précision")
ax[1].plot(seuild, rappd[1:], label="Rappel")
ax[1].plot(seuild, f1d, label="F1")
ax[1].set_title("decision_function")
ax[1].legend()

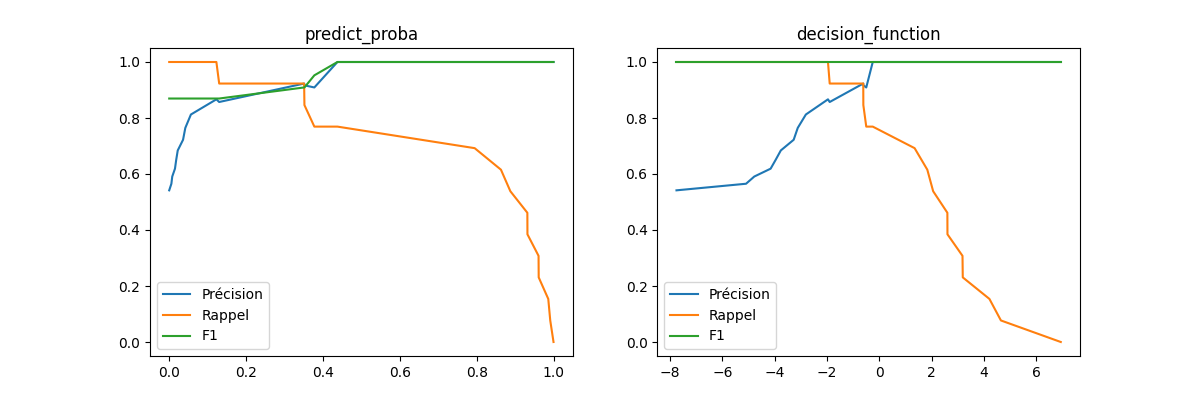
<matplotlib.legend.Legend object at 0x7f1657047820>

Pourquoi ROC alors ?

On peut se demander pourquoi on utilise la courbe ROC si d’autres graphiques sont plus compréhensibles. C’est parce que l’aire sous la courbe (AUC) est relié à un résultat important : où représente la variable aléatoire score pour une observation mal classée et la variable aléatoire score pour une observation bien classée (voir ROC).

y_pred = logreg.predict(X_test)
y_proba = logreg.predict_proba(X_test)
y_score = logreg.decision_function(X_test)


fix, ax = plt.subplots(1, 2, figsize=(12, 4))
ax[0].hist(y_proba[y_test == 0, 1], color="r", label="proba -", alpha=0.5, bins=20)
ax[0].hist(y_proba[y_test == 1, 1], color="b", label="proba +", alpha=0.5, bins=20)
ax[0].set_title("predict_proba")
ax[0].plot([0.8, 0.8], [0, 600], "--")
ax[0].legend()
ax[1].hist(y_score[y_test == 0], color="r", label="score -", alpha=0.5, bins=20)
ax[1].hist(y_score[y_test == 1], color="b", label="score +", alpha=0.5, bins=20)
ax[1].set_title("decision_function")
ax[1].plot([1, 1], [0, 250], "--")
ax[1].legend()

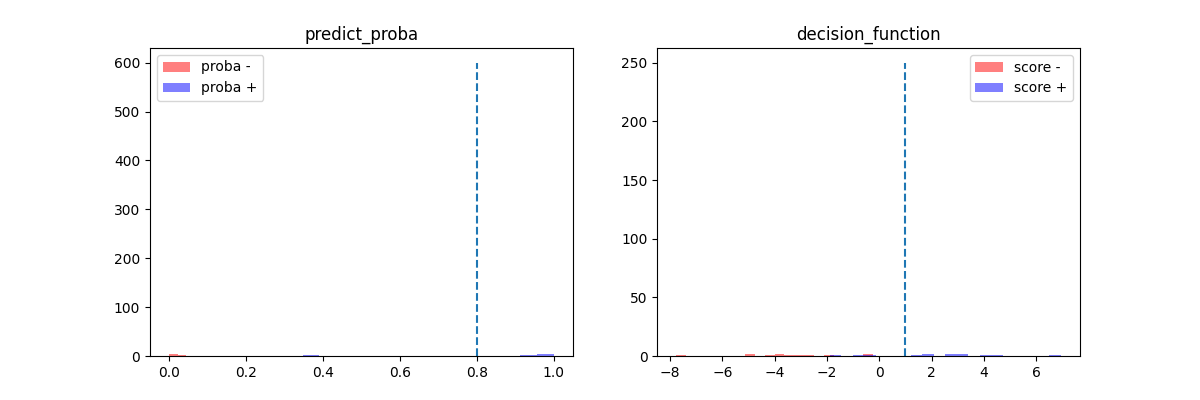
<matplotlib.legend.Legend object at 0x7f1657004eb0>

La ligne en pointillés délimité la zone à partir de laquelle le modèle est sûr de sa décision. Elle est ajusté en fonction des besoins selon qu’on a besoin de plus de rappel (seuil bas) ou plus de précision (seuil haut). Le modèle est performant si les deux histogrammes sont bien séparés. Si on note T(s) l’aire bleue après la ligne en pointillé et E(s) l’aire rouge toujours après la ligne en pointillé. Ces deux quantités sont reliées à la distribution du score pour les bonnes et mauvaises prédictions. La courbe ROC est constituée des point lorsque le seuil s varie.