Sélection des hyper-paramètres#

Le modèle des plus proches voisins KNeighborsRegressor est paramétrable. Le nombre de voisins est variables, la prédiction peut dépendre du plus proche voisins ou des $k$ plus proches proches. Comment choisir $k$ ?

[1]:

%matplotlib inline

[3]:

from teachpyx.datasets import load_wines_dataset

df = load_wines_dataset()

[4]:

import numpy.random as rnd

index = list(df.index)
rnd.shuffle(index)
df_alea = df.iloc[index, :].reset_index(drop=True)
X = df_alea.drop(["quality", "color"], axis=1)
y = df_alea["quality"]

[5]:

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y)

On fait une boucle sur un paramètre.

[6]:

from sklearn.neighbors import KNeighborsRegressor
from sklearn.model_selection import GridSearchCV
from sklearn.metrics import r2_score

voisins = []
r2s = []
for n in range(1, 10):
    knn = KNeighborsRegressor(n_neighbors=n)
    knn.fit(X_train, y_train)
    r2 = r2_score(y_test, knn.predict(X_test))
    voisins.append(n)
    r2s.append(r2)

[7]:

import pandas

df = pandas.DataFrame(dict(voisin=voisins, r2=r2s))
ax = df.plot(x="voisin", y="r2")
ax.set_title("Performance en fonction\ndu nombre de voisins");

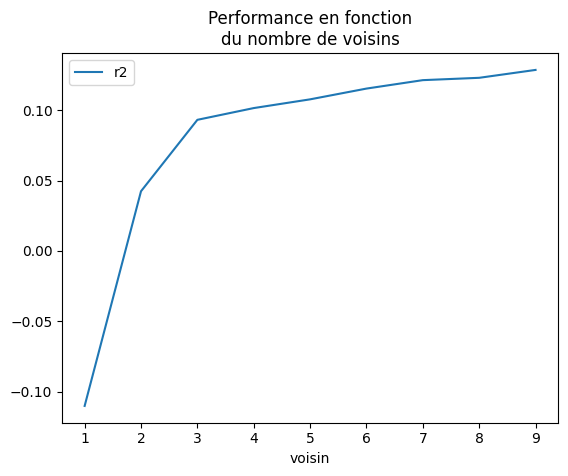
../../_images/practice_ml_winesr_knn_hyper_7_0.png

La fonction GridSearchCV automatise la recherche d’un optimum parmi les hyperparamètre, elle utilise notamment la validation croisée. On teste toutes les valeurs de $k$ de 1 à 20.

[11]:

parameters = {"n_neighbors": list(range(1, 31, 3))}

[12]:

from sklearn.neighbors import KNeighborsRegressor
from sklearn.model_selection import GridSearchCV

knn = KNeighborsRegressor()
grid = GridSearchCV(knn, parameters, verbose=2, return_train_score=True)

[13]:

grid.fit(X, y)

Fitting 5 folds for each of 10 candidates, totalling 50 fits
[CV] END ......................................n_neighbors=1; total time=   0.1s
[CV] END ......................................n_neighbors=1; total time=   0.1s
[CV] END ......................................n_neighbors=1; total time=   0.1s
[CV] END ......................................n_neighbors=1; total time=   0.0s
[CV] END ......................................n_neighbors=1; total time=   0.0s
[CV] END ......................................n_neighbors=4; total time=   0.1s
[CV] END ......................................n_neighbors=4; total time=   0.1s
[CV] END ......................................n_neighbors=4; total time=   0.1s
[CV] END ......................................n_neighbors=4; total time=   0.0s
[CV] END ......................................n_neighbors=4; total time=   0.0s
[CV] END ......................................n_neighbors=7; total time=   0.1s
[CV] END ......................................n_neighbors=7; total time=   0.1s
[CV] END ......................................n_neighbors=7; total time=   0.1s
[CV] END ......................................n_neighbors=7; total time=   0.0s
[CV] END ......................................n_neighbors=7; total time=   0.1s
[CV] END .....................................n_neighbors=10; total time=   0.1s
[CV] END .....................................n_neighbors=10; total time=   0.1s
[CV] END .....................................n_neighbors=10; total time=   0.1s
[CV] END .....................................n_neighbors=10; total time=   0.1s
[CV] END .....................................n_neighbors=10; total time=   0.1s
[CV] END .....................................n_neighbors=13; total time=   0.1s
[CV] END .....................................n_neighbors=13; total time=   0.1s
[CV] END .....................................n_neighbors=13; total time=   0.1s
[CV] END .....................................n_neighbors=13; total time=   0.1s
[CV] END .....................................n_neighbors=13; total time=   0.1s
[CV] END .....................................n_neighbors=16; total time=   0.1s
[CV] END .....................................n_neighbors=16; total time=   0.1s
[CV] END .....................................n_neighbors=16; total time=   0.1s
[CV] END .....................................n_neighbors=16; total time=   0.1s
[CV] END .....................................n_neighbors=16; total time=   0.1s
[CV] END .....................................n_neighbors=19; total time=   0.1s
[CV] END .....................................n_neighbors=19; total time=   0.1s
[CV] END .....................................n_neighbors=19; total time=   0.1s
[CV] END .....................................n_neighbors=19; total time=   0.1s
[CV] END .....................................n_neighbors=19; total time=   0.1s
[CV] END .....................................n_neighbors=22; total time=   0.1s
[CV] END .....................................n_neighbors=22; total time=   0.1s
[CV] END .....................................n_neighbors=22; total time=   0.1s
[CV] END .....................................n_neighbors=22; total time=   0.1s
[CV] END .....................................n_neighbors=22; total time=   0.1s
[CV] END .....................................n_neighbors=25; total time=   0.1s
[CV] END .....................................n_neighbors=25; total time=   0.1s
[CV] END .....................................n_neighbors=25; total time=   0.1s
[CV] END .....................................n_neighbors=25; total time=   0.1s
[CV] END .....................................n_neighbors=25; total time=   0.1s
[CV] END .....................................n_neighbors=28; total time=   0.1s
[CV] END .....................................n_neighbors=28; total time=   0.1s
[CV] END .....................................n_neighbors=28; total time=   0.1s
[CV] END .....................................n_neighbors=28; total time=   0.1s
[CV] END .....................................n_neighbors=28; total time=   0.1s

[13]:

GridSearchCV(estimator=KNeighborsRegressor(),
             param_grid={'n_neighbors': [1, 4, 7, 10, 13, 16, 19, 22, 25, 28]},
             return_train_score=True, verbose=2)

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

[14]:

res = grid.cv_results_
k = res["param_n_neighbors"]
train_score = res["mean_train_score"]
test_score = res["mean_test_score"]

import pandas

df_score = pandas.DataFrame(dict(k=k, test=test_score, train=train_score))
ax = df_score.plot(x="k", y="train", figsize=(6, 4))
df_score.plot(x="k", y="test", ax=ax, grid=True)
ax.set_title(
    "Evolution de la performance sur\nles bases d'apprentissage et de test"
    + "\nen fonction du nombre de voisins"
)
ax.set_ylabel("r2");

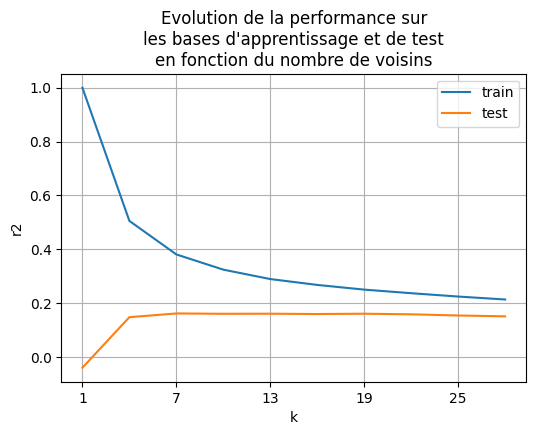
../../_images/practice_ml_winesr_knn_hyper_12_0.png

On voit que le modèle gagne en pertinence sur la base de test et que le nombre de voisins optimal parmi ceux essayés se situe autour de 15.

[15]:

df_score[12:17]

[15]:

	k	test	train

L’erreur sur la base d’apprentissage augmente de manière sensible ( $R^2$ baisse). Voyons ce qu’il en est un peu plus loin.

[22]:

parameters = {"n_neighbors": list(range(5, 51, 10)) + list(range(50, 151, 50))}
grid = GridSearchCV(knn, parameters, verbose=2, return_train_score=True)
grid.fit(X, y)

Fitting 5 folds for each of 8 candidates, totalling 40 fits
[CV] END ......................................n_neighbors=5; total time=   0.1s
[CV] END ......................................n_neighbors=5; total time=   0.0s
[CV] END ......................................n_neighbors=5; total time=   0.1s
[CV] END ......................................n_neighbors=5; total time=   0.1s
[CV] END ......................................n_neighbors=5; total time=   0.2s
[CV] END .....................................n_neighbors=15; total time=   0.1s
[CV] END .....................................n_neighbors=15; total time=   0.1s
[CV] END .....................................n_neighbors=15; total time=   0.1s
[CV] END .....................................n_neighbors=15; total time=   0.1s
[CV] END .....................................n_neighbors=15; total time=   0.1s
[CV] END .....................................n_neighbors=25; total time=   0.2s
[CV] END .....................................n_neighbors=25; total time=   0.1s
[CV] END .....................................n_neighbors=25; total time=   0.1s
[CV] END .....................................n_neighbors=25; total time=   0.1s
[CV] END .....................................n_neighbors=25; total time=   0.1s
[CV] END .....................................n_neighbors=35; total time=   0.1s
[CV] END .....................................n_neighbors=35; total time=   0.1s
[CV] END .....................................n_neighbors=35; total time=   0.1s
[CV] END .....................................n_neighbors=35; total time=   0.1s
[CV] END .....................................n_neighbors=35; total time=   0.1s
[CV] END .....................................n_neighbors=45; total time=   0.1s
[CV] END .....................................n_neighbors=45; total time=   0.1s
[CV] END .....................................n_neighbors=45; total time=   0.1s
[CV] END .....................................n_neighbors=45; total time=   0.1s
[CV] END .....................................n_neighbors=45; total time=   0.1s
[CV] END .....................................n_neighbors=50; total time=   0.1s
[CV] END .....................................n_neighbors=50; total time=   0.1s
[CV] END .....................................n_neighbors=50; total time=   0.1s
[CV] END .....................................n_neighbors=50; total time=   0.1s
[CV] END .....................................n_neighbors=50; total time=   0.2s
[CV] END ....................................n_neighbors=100; total time=   0.1s
[CV] END ....................................n_neighbors=100; total time=   0.2s
[CV] END ....................................n_neighbors=100; total time=   0.2s
[CV] END ....................................n_neighbors=100; total time=   0.1s
[CV] END ....................................n_neighbors=100; total time=   0.2s
[CV] END ....................................n_neighbors=150; total time=   0.2s
[CV] END ....................................n_neighbors=150; total time=   0.1s
[CV] END ....................................n_neighbors=150; total time=   0.2s
[CV] END ....................................n_neighbors=150; total time=   0.1s
[CV] END ....................................n_neighbors=150; total time=   0.2s

[22]:

GridSearchCV(estimator=KNeighborsRegressor(),
             param_grid={'n_neighbors': [5, 15, 25, 35, 45, 50, 100, 150]},
             return_train_score=True, verbose=2)

[23]:

res = grid.cv_results_
k = res["param_n_neighbors"]
train_score = res["mean_train_score"]
test_score = res["mean_test_score"]

import pandas

df_score = pandas.DataFrame(dict(k=k, test=test_score, train=train_score))
ax = df_score.plot(x="k", y="train", figsize=(6, 4))
df_score.plot(x="k", y="test", ax=ax, grid=True)
ax.set_title(
    "Evolution de la performance sur\nles bases d'apprentissage et de test"
    + "\nen fonction du nombre de voisins"
)
ax.set_ylabel("r2");

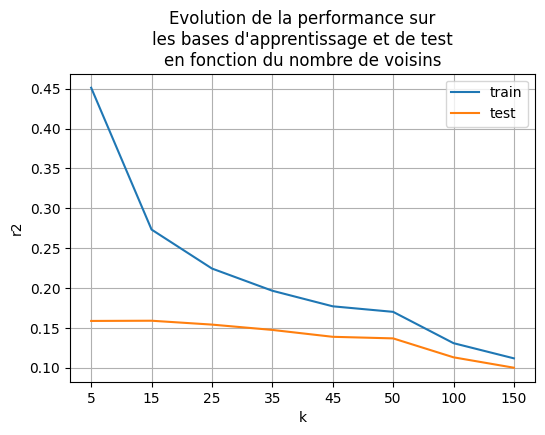
../../_images/practice_ml_winesr_knn_hyper_17_0.png

Après 25 voisins, la pertinence du modèle décroît fortement, ce qui paraît normal car plus il y a de voisins, moins la prédiction est locale en quelque sorte. Pour ce modèle, les plus proches voisins, l’erreur sur la base d’apprentissage ne fait que décroître. $R^2$ est maximal pour $k=1$ puisqu’on prédit avec le plus proche voisin, c’est-à-dire lui-même.

Notebook on github