Arbre et Trie

Le mot trie est anglais et se prononce traïlle. Il sera défini plus bas. Cette structure de données est très adaptée à la recherche d’un mot dans une liste ordonnée. C’est aussi une histoire de dictionnaires imbriqués.

Rechercher un mot dans une liste est un problème simple. Et pourtant, cette tâche peut être plus ou moins rapide selon la façon dont on représente cette liste, voire de la compresser. L’objectif est ici de découvrir trois façons de construire un ensemble de mots avec des dictionnaires et des listes. La recherche d’un mot dans cet ensemble sera différente à chaque fois. On veut mesurer le temps qu’il faut pour vérifier qu’un mot appartient à une liste de mots de trois façons différentes et à partir de trois représentations différentes :

• liste de mots

• liste triée de mots

• trie

A quoi ça sert : voir Complétion.

Construction d’une liste aléatoire

Plutôt que de charger un texte en mémoire, on construit des mots aléatoirement.

Exercice 1

A partir de la fonction suivante, construit une liste aléatoire de 10000 mots d’une longueur de 20 lettres.

import random


def mot_alea(l):
    l = [chr(97 + random.randint(0, 25)) for i in range(l)]
    return "".join(l)

Exercice 2

Les listes ont une méthode index qui permet de retrouver la position d’un mot (elle effectue donc une recherche). Le module time possède une fonction clock. Utiliser cette fonction pour mesurer le temps du code suivant (qu’on prendra soin d’exécuter plusieurs fois en boucle afin d’avoir une mesure fiable) :

list_exercice_1 = mot_alea(10)

for k in list_exercice_1:
    i = list_exercice_1.index(k)

IPython propose une commande magique pour mesure le temps d’exécution d’une instruction : %timeit qui exécute cette instruction plusieurs fois avant de retourner un résultat.

Recherche dichotomique

Lors des premières séances de TD, on a implémenté la recherche dichotomique. La liste de mots est triée. Vous pouvez soit retrouver le code cette fonction depuis ce TD soit implémenter de nouveau la fonction.

Exercice 3

L’objectif est de mesurer le temps pris par la recherche dichotomique appliquée à la même liste que celle de l’exercice 1 (mais triée).

Exercice 4

Mesurer le temps de calcul lorsque la recherche d’un mot est effectuée 1000 fois pour des tailles de liste de 10, 100, 1000, 10000, 100000 mots. On fait ceci pour la recherche simple et la recherche dichotomique. Vérifier que cela correspond au coût des deux algorithmes (qu’on précisera).

Trie

Le coût des deux recherches dépendent du nombre de mots dans la liste. Il est possible de construire une structure de données qui fait dépendre le coût de cette recherche du nombre de lettres différentes (26) et de la longueur maximale des mots.

Le trie suivant représente les mots A, to, tea, ted, ten, inn. Chaque noeud final est un mot.

from IPython.display import Image

Image("wiki_trie.png")

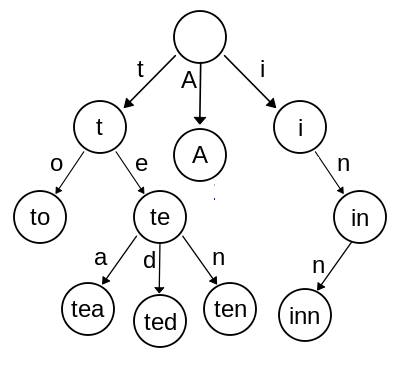
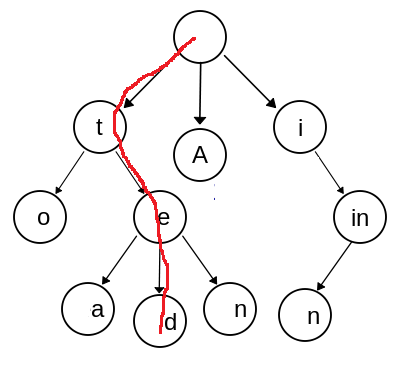
Dans un vrai trie, on ne conserve que la dernière lettre dans chaque noeud, un mot de la liste est obtenu en parcourant un chemin qui va du noeud racine jusqu’à une feuille. Plus bas, un exemple pour ted.

Image("wiki_trie2.png")

Exercice 5

Construire cette structure. Les classes sont une possibilité mais ne sont pas indispensables.

Recherche dans un trie

Exercice 6

Une fois qu’on a la structure, il faut aussi écrire la fonction qui recherche un mot dans le trie.

Exercice 7

Il ne reste plus qu’à mesurer le temps.

---

Notebook on github