Plus proches voisins en grande dimension - correction#

La méthodes des plus proches voisins est un algorithme assez simple qui devient très lent en grande dimension. Ce notebook propose un moyen d’aller plus vite (ACP) mais en perdant un peu en performance.

[1]:

%matplotlib inline

Q1 : k-nn : mesurer la performance#

[2]:

import time
from sklearn.datasets import make_classification
from sklearn.neighbors import KNeighborsClassifier


def what_to_measure(
    n,
    n_features,
    n_classes=3,
    n_clusters_per_class=2,
    n_informative=8,
    neighbors=5,
    algorithm="brute",
):
    datax, datay = make_classification(
        n,
        n_features=n_features,
        n_classes=n_classes,
        n_clusters_per_class=n_clusters_per_class,
        n_informative=n_informative,
    )
    model = KNeighborsClassifier(neighbors, algorithm=algorithm)
    model.fit(datax, datay)
    t1 = time.perf_counter()
    y = model.predict(datax)
    t2 = time.perf_counter()
    return t2 - t1, y

[3]:

dt, y = what_to_measure(2000, 10)
dt

[3]:

0.07576929999959248

dimension#

[4]:

nf_set = [10, 20, 50, 100, 200]  # , 200, 500, 1000] # , 2000, 5000, 10000]
Nobs = 500

[5]:

x = []
y = []
ys = []
for nf in nf_set:
    x.append(nf)
    dt, _ = what_to_measure(Nobs, n_features=nf)
    y.append(dt)
    if nf <= 100:
        dt2, _ = what_to_measure(Nobs, n_features=nf, algorithm="ball_tree")
    else:
        dt2 = None
    ys.append(dt2)
    print("nf={0} dt={1} dt2={2}".format(nf, dt, dt2))

nf=10 dt=0.0035799999996015686 dt2=0.08653190000040922
nf=20 dt=0.010255199999846809 dt2=0.11729259999992792
nf=50 dt=0.005994999999529682 dt2=0.11148469999989175
nf=100 dt=0.004818200000045181 dt2=0.12828609999996843
nf=200 dt=0.005615799999759474 dt2=None

[6]:

import matplotlib.pyplot as plt

fig, ax = plt.subplots(1, 1)
ax.plot(x, y, "o-", label="brute")
ax.plot(x, ys, "o-", label="ball_tree")
ax.set_xlabel("number of features")
ax.set_ylabel("prediction time in seconds")
ax.legend();

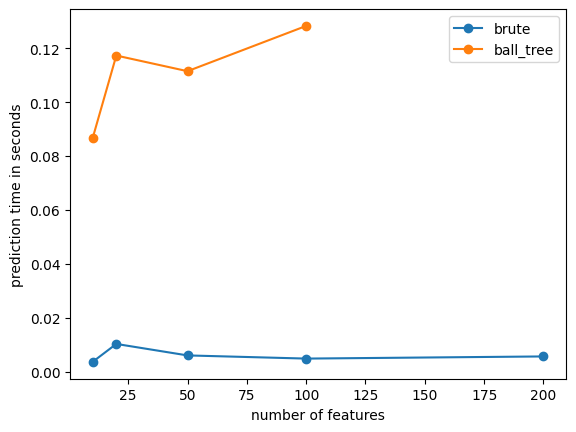
../../_images/practice_tds-algo_knn_high_dimension_correction_8_0.png

observations#

[7]:

x = []
y = []
ys = []
for nobs in [Nobs // 2, Nobs, Nobs * 2]:
    x.append(nobs)
    dt, _ = what_to_measure(nobs, n_features=200)
    y.append(dt)
    if nobs <= 5000:
        dt2, _ = what_to_measure(nobs, n_features=200, algorithm="ball_tree")
    else:
        dt2 = None
    ys.append(dt2)
    print("nobs={0} dt={1} dt2={2}".format(nobs, dt, dt2))

nobs=250 dt=0.0024919999996200204 dt2=0.04157219999979134
nobs=500 dt=0.007431699999870034 dt2=0.11408440000013798
nobs=1000 dt=0.0051083999996990315 dt2=0.3907441999999719

[8]:

fig, ax = plt.subplots(1, 1)
ax.plot(x, y, "o-", label="brute")
ax.plot(x, ys, "o-", label="ball_tree")
ax.set_xlabel("number of observations")
ax.set_ylabel("prediction time in seconds")
ax.legend();

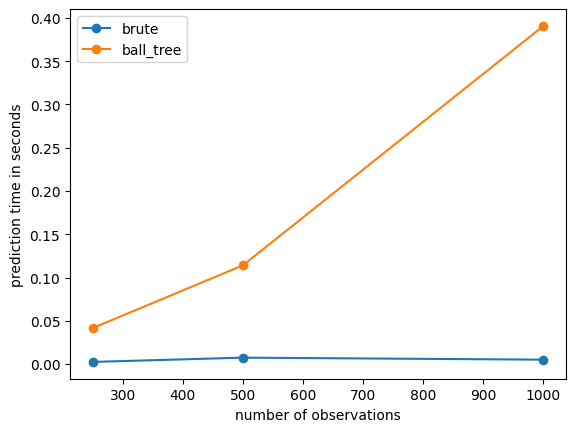
../../_images/practice_tds-algo_knn_high_dimension_correction_11_0.png

Q2 : k-nn avec sparse features#

On recommence cette mesure de temps mais en créant des jeux de données sparses. On utilise le jeu précédent et on lui adjoint des coordonnées aléatoires et sparse. La première fonction random_sparse_matrix crée un vecteur sparse.

[9]:

import numpy
import numpy.random
import random
import scipy.sparse


def random_sparse_matrix(shape, ratio_sparse=0.2):
    rnd = numpy.random.rand(shape[0] * shape[1])
    sparse = 0
    for i in range(0, len(rnd)):
        x = random.random()
        if x <= ratio_sparse - sparse:
            sparse += 1 - ratio_sparse
        else:
            rnd[i] = 0
            sparse -= ratio_sparse
    rnd.resize(shape[0], shape[1])
    return scipy.sparse.csr_matrix(rnd)


mat = random_sparse_matrix((20, 20))
"% non null coefficient", 1.0 * mat.nnz / (
    mat.shape[0] * mat.shape[1]
), "shape", mat.shape

[9]:

('% non null coefficient', 0.2, 'shape', (20, 20))

[10]:

import random
from scipy.sparse import hstack


def what_to_measure_sparse(
    n,
    n_features,
    n_classes=3,
    n_clusters_per_class=2,
    n_informative=8,
    neighbors=5,
    algorithm="brute",
    nb_sparse=20,
    ratio_sparse=0.2,
):
    datax, datay = make_classification(
        n,
        n_features=n_features,
        n_classes=n_classes,
        n_clusters_per_class=n_clusters_per_class,
        n_informative=n_informative,
    )

    sp = random_sparse_matrix(
        (datax.shape[0], (nb_sparse - n_features)), ratio_sparse=ratio_sparse
    )
    datax = hstack([datax, sp])
    model = KNeighborsClassifier(neighbors, algorithm=algorithm)
    model.fit(datax, datay)
    t1 = time.perf_counter()
    y = model.predict(datax)
    t2 = time.perf_counter()
    return t2 - t1, y, datax.nnz / (datax.shape[0] * datax.shape[1])

[11]:

dt, y, sparse_ratio = what_to_measure_sparse(Nobs, 10, nb_sparse=100, ratio_sparse=0.2)
dt, sparse_ratio

[11]:

(0.16139359999942826, 0.28)

Seul l’algorithme brute accepte les features sparses.

[12]:

from tqdm import tqdm

x = []
y = []
nfd = 200
for nf in nf_set:
    x.append(nf)
    dt, _, ratio = what_to_measure_sparse(
        Nobs, n_features=nf, nb_sparse=nfd + nf, ratio_sparse=1.0 * nfd / (nfd + nf)
    )
    y.append(dt)
    print("nf={0} dt={1} ratio={2}".format(nf, dt, ratio))

nf=10 dt=4.16765100000066 ratio=0.9546476190476191
nf=20 dt=4.157290099999955 ratio=0.9173545454545454
nf=50 dt=4.374867700000323 ratio=0.84
nf=100 dt=5.37886189999972 ratio=0.7777733333333333
nf=200 dt=9.63584069999979 ratio=0.75

[13]:

fig, ax = plt.subplots(1, 1)
ax.plot(x, y, "o-", label="brute")
ax.set_xlabel("number of dimensions")
ax.set_ylabel("prediction time in seconds")
ax.legend();

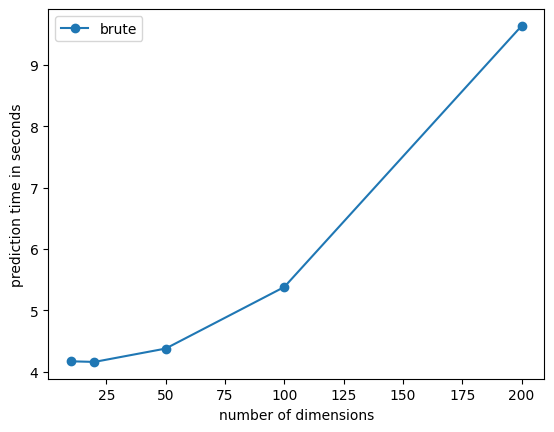
../../_images/practice_tds-algo_knn_high_dimension_correction_18_0.png

La dimension augmente mais le nombre de features non nulle est constant. Comme l’algorithme est fortement dépendant de la distance entre deux éléments et le coût de cette distance dépend du nombre de coefficients non nuls.

Q3 : Imaginez une façon d’aller plus vite ?#

Le coût d’un algorithme des plus proches voisins est linéaire selon la dimension car la majeure partie du temps est passé dans la fonction de distance et que celle-ci est linéaire. Mesurons la performance en fonction de la dimension. Ce n’est pas vraiment rigoureux de le faire dans la mesure où les données changent et n’ont pas les mêmes propriétés mais cela donnera une idée.

[14]:

from sklearn.model_selection import train_test_split


def what_to_measure_perf(
    n,
    n_features,
    n_classes=3,
    n_clusters_per_class=2,
    n_informative=8,
    neighbors=5,
    algorithm="brute",
):
    datax, datay = make_classification(
        n,
        n_features=n_features,
        n_classes=n_classes,
        n_clusters_per_class=n_clusters_per_class,
        n_informative=n_informative,
    )
    X_train, X_test, y_train, y_test = train_test_split(datax, datay)
    model = KNeighborsClassifier(neighbors, algorithm=algorithm)
    model.fit(X_train, y_train)
    t1 = time.perf_counter()
    y = model.predict(X_test)
    t2 = time.perf_counter()
    good = (y_test == y).sum() / len(datay)
    return t2 - t1, good


what_to_measure_perf(Nobs, 100)

[14]:

(0.0014494000006379792, 0.18)

[15]:

x = []
y = []
for nf in nf_set:
    x.append(nf)
    dt, perf = what_to_measure_perf(Nobs, n_features=nf)
    y.append(perf)
    print("nf={0} perf={1} dt={2}".format(nf, perf, dt))

nf=10 perf=0.212 dt=0.0015942999998515006
nf=20 perf=0.19 dt=0.0019345000000612345
nf=50 perf=0.186 dt=0.002628500000355416
nf=100 perf=0.164 dt=0.001998000000639877
nf=200 perf=0.15 dt=0.0025021000001288485

[16]:

fig, ax = plt.subplots(1, 1)
ax.plot(x, y, "o-", label="brute")
ax.set_xlabel("number of dimensions")
ax.set_ylabel("% good classification")
ax.legend();

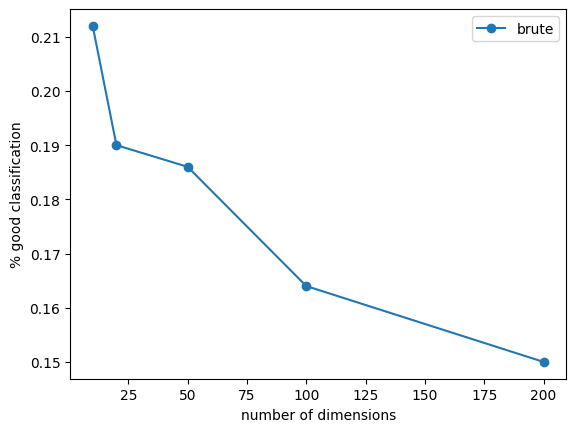
../../_images/practice_tds-algo_knn_high_dimension_correction_23_0.png

Même si les performances ne sont pas tout-à-fait comparables, il est vrai qu’il est plus difficile de construire un classifieur basé sur une distance en grande dimension. La raison est simple : plus il y a de dimensions, plus la distance devient binaire : soit les coordonnées concordent sur les mêmes dimensions, soit elles ne concordent pas et la distance est presque équivalente à la somme des carrés des coordonnées.

Revenons au problème principal. Accélérer le temps de calcul des plus proches voisins. L’idée est d’utiliser une ACP : l’ACP a la propriété de trouver un hyperplan qui réduit les dimensions mais qui conserve le plus possible l’inertie d’un nuage de points et on l’exprimer ainsi :

$I = \frac{1}{n} \sum_i^n \left\Vert X_i - G \right\Vert^2 = \frac{1}{n^2} \sum_i^n\sum_j^n \left\Vert X_i - X_j \right\Vert^2$

Bref, l’ACP conserve en grande partie les distances. Cela veut dire qu’une ACP réduit les dimensions, donc le temps de prédiction, tout en conservant le plus possible la distance entre deux points.

[17]:

from sklearn.decomposition import PCA


def what_to_measure_perf_acp(
    n,
    n_features,
    acp_dim=10,
    n_classes=3,
    n_clusters_per_class=2,
    n_informative=8,
    neighbors=5,
    algorithm="brute",
):
    datax, datay = make_classification(
        n,
        n_features=n_features,
        n_classes=n_classes,
        n_clusters_per_class=n_clusters_per_class,
        n_informative=n_informative,
    )
    X_train, X_test, y_train, y_test = train_test_split(datax, datay)

    # sans ACP
    model = KNeighborsClassifier(neighbors, algorithm=algorithm)
    model.fit(X_train, y_train)
    t1o = time.perf_counter()
    y = model.predict(X_test)
    t2o = time.perf_counter()
    goodo = (y_test == y).sum() / len(datay)

    # ACP
    model = KNeighborsClassifier(neighbors, algorithm=algorithm)
    pca = PCA(n_components=acp_dim)
    t0 = time.perf_counter()
    X_train_pca = pca.fit_transform(X_train)
    model.fit(X_train_pca, y_train)
    t1 = time.perf_counter()
    X_test_pca = pca.transform(X_test)
    y = model.predict(X_test_pca)
    t2 = time.perf_counter()
    good = (y_test == y).sum() / len(datay)

    return t2o - t1o, goodo, t2 - t1, t1 - t0, good


what_to_measure_perf_acp(500, 100)

[17]:

(0.002483399999618996, 0.196, 0.06338310000046476, 0.22452249999969354, 0.21)

[18]:

x = []
y = []
yp = []
p = []
p_noacp = []
y_noacp = []
for nf in nf_set:
    x.append(nf)
    dt_noacp, perf_noacp, dt, dt_train, perf = what_to_measure_perf_acp(
        Nobs, n_features=nf
    )
    p.append(perf)
    y.append(perf)
    yp.append(dt_train)
    y_noacp.append(dt_noacp)
    p_noacp.append(perf_noacp)
    print("nf={0} perf={1} dt_predict={2} dt_train={3}".format(nf, perf, dt, dt_train))

nf=10 perf=0.21 dt_predict=0.0015590000002703164 dt_train=0.0045598999995490885
nf=20 perf=0.22 dt_predict=0.0020978000002287445 dt_train=0.003090600000177801
nf=50 perf=0.168 dt_predict=0.10930980000011914 dt_train=0.009109900000112248
nf=100 perf=0.182 dt_predict=0.05428739999933896 dt_train=0.13726130000031844
nf=200 perf=0.198 dt_predict=0.0553301999998439 dt_train=0.046151300000019546

[19]:

fig, ax = plt.subplots(1, 2, figsize=(12, 5))
ax[0].plot(x, y, "o-", label="prediction time with PCA")
ax[0].plot(x, yp, "o-", label="training time with PCA")
ax[0].plot(x, y_noacp, "o-", label="prediction time no PCA")
ax[0].set_xlabel("number of dimensions")
ax[0].set_ylabel("time")
ax[1].plot(x, p, "o-", label="with PCA")
ax[1].plot(x, p_noacp, "o-", label="no PCA")
ax[1].set_xlabel("number of dimensions")
ax[1].set_ylabel("% good classification")
ax[0].legend()
ax[1].legend();

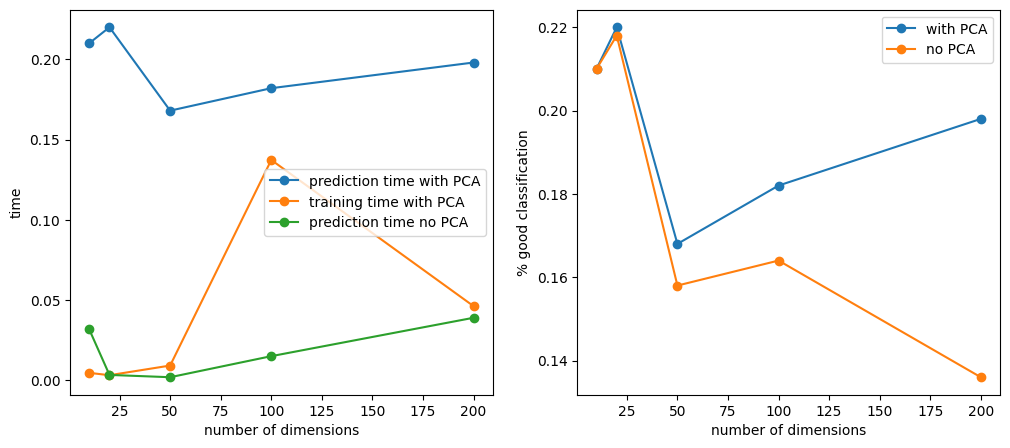
../../_images/practice_tds-algo_knn_high_dimension_correction_27_0.png

Etonnament, l’ACP améliore les performances du modèle en terme de prédiction. Cela suggère que les données sont bruitées et que l’ACP en a réduit l’importance. Le calcul de l’ACP est linéaire par rapport au nombre de features. Une partie des coûts a été transférée sur l’apprentissage et le prédiction est constant car on conseerve toujours le même nombre de dimensions.

Notebook on github