Variables, boucles, tests (correction)¶

Boucles, tests, correction.

Partie 3 : boucles (exercice)¶

[1]:

l = [4, 3, 0, 2, 1]
i = 0
while l[i] != 0:
    i = l[i]
    print(i)  # que vaut l[i] à la fin ?

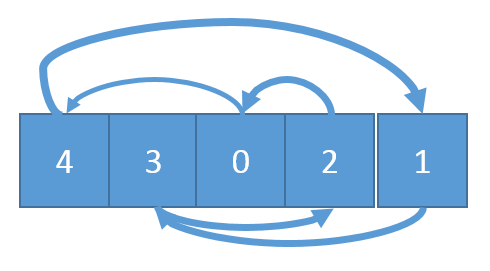
Cet exercice montre une façon curieuse de se déplacer dans un tableau puisqu’on commence à la première position puis on va la position indiqué par le premier élément du tableau et ainsi de suite. On s’arrête quand on tombe sur la valeur zéro.

[2]:

from IPython.display import Image

Image("td2_1.png")

[2]:

../../_images/practice_tds-base_variable_boucle_tests_correction_4_0.png

Partie 5 : recherche non dichotomique (exercice)¶

Il n’y a pas d’autres moyens que de passer tous les éléments en revue et de conserver la position du premier élément dans la liste qui vérifie le critère de recherche.

[3]:

l = [3, 6, 2, 7, 9]
x = 7

for i, v in enumerate(l):
    if v == x:
        position = i

print(position)

Partie 6 : recherche dichotomique (exercice)¶

La recherche dichotomique s’applique uniquement sur un tableau triée. A chaque itération, on vise le milieu du tableau pour savoir dans quelle moitié chercher.

[4]:

l = [2, 3, 6, 7, 9]
# si la liste n'est pas triée, il faut écrire :
l.sort()
x = 7

a = 0
b = len(l) - 1
while a <= b:
    m = (a + b) // 2  # ne pas oublier // sinon la division est réelle
    if l[m] == x:
        position = m  # ligne A
        break  # pas la peine de continuer, on quitte la boucle
    elif l[m] < x:
        a = m + 1
    else:
        b = m - 1

print(position)

Partie 7 : pour aller plus loin (exercice)¶

Lorsque l’élément à chercher n’est pas dans la liste, cela déclenche une erreur :

[5]:

l = [2, 3, 6, 7, 9]
l.sort()
x = 5

position = -1

a = 0
b = len(l) - 1
while a <= b:
    m = (a + b) // 2
    if l[m] == x:
        position = m
        break
    elif l[m] < x:
        a = m + 1
    else:
        b = m - 1

print(position)

-1

Le programme affiche None qui était la valeur par défaut de la variable position. La boucle n’a pas changé le contenu de la variable. Donc, lorsque position==-1, cela veut dire que le résultat n’a pas été trouvé.

Coût

Comme à chaque itération, on divise la taille du problème par deux, on est sûr que l’algorithme a trouvé la réponse lorsque $\frac{n}{2^k} < 1$ où $n$ est le nombre d’éléments du tableau et $k$ le nombre d’itérations. Par conséquent, $k \sim \ln_2 n$ . On note cela $O(\ln_2 n)$ . Le programme suivant vérifie cela :

[6]:

import random, math

l = list(range(0, 1000000))

for k in range(0, 10):
    x = random.randint(0, l[-1])

    iter = 0
    a = 0
    b = len(l) - 1
    while a <= b:
        iter += 1
        m = (a + b) // 2
        if l[m] == x:
            position = m
            break
        elif l[m] < x:
            a = m + 1
        else:
            b = m - 1

    print(
        "k=",
        k,
        "x=",
        x,
        "itération=",
        iter,
        " log2(len(l))=",
        math.log(len(l)) / math.log(2),
    )

k= 0 x= 456217 itération= 20  log2(len(l))= 19.931568569324174
k= 1 x= 134146 itération= 20  log2(len(l))= 19.931568569324174
k= 2 x= 166639 itération= 16  log2(len(l))= 19.931568569324174
k= 3 x= 922092 itération= 19  log2(len(l))= 19.931568569324174
k= 4 x= 728522 itération= 20  log2(len(l))= 19.931568569324174
k= 5 x= 162931 itération= 15  log2(len(l))= 19.931568569324174
k= 6 x= 741312 itération= 20  log2(len(l))= 19.931568569324174
k= 7 x= 195045 itération= 20  log2(len(l))= 19.931568569324174
k= 8 x= 642304 itération= 18  log2(len(l))= 19.931568569324174
k= 9 x= 685730 itération= 20  log2(len(l))= 19.931568569324174

[ ]:

Notebook on github