Plus court chemin passant par tous les noeuds d’un graphe¶
Dans le cas présent, le graphe est totalement connecté puisque chaque noeud est connecté à tous les autres. On commence par tiré des villes aléatoires.
Distance¶
[2]:
import numpy
def random_cities(n):
return numpy.random.randn(n, 2)
random_cities(3)
[2]:
array([[ 1.39190158, 0.70104769],
[-0.865672 , 1.22913836],
[ 1.65596723, -0.32503514]])
Ensuite vient la distance du circuit avec les villes dans l’ordre dans lequel elles apparaissent.
[3]:
def distance_boucle(cities):
d = 0
for i in range(cities.shape[0]):
dx = cities[i - 1, 0] - cities[i, 0]
dy = cities[i - 1, 1] - cities[i, 1]
d += (dx**2 + dy**2) ** 0.5
return d
cities = numpy.array([[0, 0], [1, 1]])
distance_boucle(cities)
[3]:
2.8284271247461903
La même fonction sans boucle et avec numpy.
[4]:
def distance(cities):
d = ((cities[:-1] - cities[1:]) ** 2).sum(axis=1) ** 0.5
d2 = ((cities[0] - cities[-1]) ** 2).sum() ** 0.5
return d.sum() + d2
cities = numpy.array([[0, 0], [0, 2], [2, 2], [2, 0]])
distance(cities)
[4]:
8.0
On mesure de chaque calcul de distance sur un petit échantillon.
[10]:
%timeit -r 10 -n 1000 distance_boucle(cities)
25.4 µs ± 6.29 µs per loop (mean ± std. dev. of 10 runs, 1,000 loops each)
[11]:
%timeit -r 10 -n 1000 distance(cities)
28.5 µs ± 6.93 µs per loop (mean ± std. dev. of 10 runs, 1,000 loops each)
C’est pareil. Et maintenant sur un plus grand jeu.
[12]:
cities = random_cities(1000)
[15]:
%timeit -r 10 -n 10 distance_boucle(cities)
1.72 ms ± 513 µs per loop (mean ± std. dev. of 10 runs, 10 loops each)
[16]:
%timeit -r 10 -n 10 distance(cities)
The slowest run took 11.82 times longer than the fastest. This could mean that an intermediate result is being cached.
220 µs ± 253 µs per loop (mean ± std. dev. of 10 runs, 10 loops each)
La différence est clairement en faveur de numpy.
Idée d’algorithme¶
On parcourt toutes les permutations et on garde la meilleure. Cela fonctionnera si le nombre de villes est très petit mais cela peut servir plus tard
[17]:
from itertools import permutations
def optimise(cities):
best_cities = None
best_distance = None
indices = list(range(cities.shape[0]))
for p in permutations(indices):
p_cities = cities[p, :]
d = distance(p_cities)
if best_distance is None or d < best_distance:
best_distance = d
best_cities = p_cities
return best_cities, best_distance
cities = numpy.array([[0, 0], [0, 2], [2, 2], [2, 0]])
optimise(cities)
[17]:
(array([[0, 0],
[0, 2],
[2, 2],
[2, 0]]),
8.0)
On dessine car le résultat est plus facilement vérifiable.
[18]:
import matplotlib.pyplot as plt
fig, ax = plt.subplots(1, 1, figsize=(2, 2))
cities = random_cities(7)
opt_cities = optimise(cities)[0]
ax.plot(
list(opt_cities[:, 0]) + [opt_cities[0, 0]],
list(opt_cities[:, 1]) + [opt_cities[0, 1]],
"o-",
);
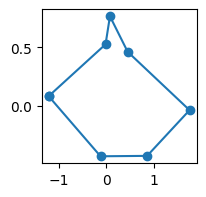
Comme ça prend trop de temps, on tire au hasard des permutations, un nombre fini pour être sûr que l’algorithme se termine en un temps raisonnable.
[20]:
def optimise_random(cities, n_perm):
best_cities = None
best_distance = None
indices = list(range(cities.shape[0]))
for i in range(n_perm):
p = numpy.random.permutation(indices)
p_cities = cities[p, :]
d = distance(p_cities)
if best_distance is None or d < best_distance:
best_distance = d
best_cities = p_cities
return best_cities, best_distance
cities = numpy.array([[0, 0], [0, 2], [2, 2], [2, 0]])
optimise_random(cities, 10)
[20]:
(array([[0, 2],
[2, 2],
[2, 0],
[0, 0]]),
8.0)
[21]:
fig, ax = plt.subplots(1, 1, figsize=(3, 3))
cities = random_cities(10)
opt_cities = optimise_random(cities, 10000)[0]
ax.plot(
list(opt_cities[:, 0]) + [opt_cities[0, 0]],
list(opt_cities[:, 1]) + [opt_cities[0, 1]],
"o-",
);
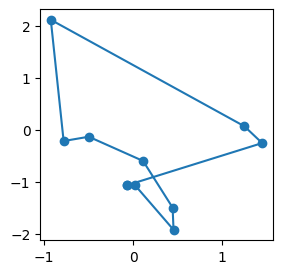
Mais ce n’est pas parfait car il y a des croisements.
Croisements¶
On écrit une fonction pour enlever des erreurs évidentes. La solution obtenue sera meilleure sans poutant être optimale.
[23]:
def retournement1(cities):
d0 = distance(cities)
for i in range(cities.shape[0] - 1):
for j in range(i + 1, cities.shape[0]):
cities[i : j + 1, :] = cities[i : j + 1, :][::-1]
d = distance(cities)
if d < d0:
d0 = d
else:
cities[i : j + 1, :] = cities[i : j + 1, :][::-1]
return cities
cities = numpy.array([[0, 0], [0, 2], [2, 2], [2, 0]])
retournement1(cities)
[23]:
array([[0, 0],
[0, 2],
[2, 2],
[2, 0]])
[31]:
fig, ax = plt.subplots(1, 2, figsize=(6, 3))
cities = random_cities(20)
opt_cities = optimise_random(cities, 10000)[0]
ax[0].plot(
list(opt_cities[:, 0]) + [opt_cities[0, 0]],
list(opt_cities[:, 1]) + [opt_cities[0, 1]],
"or-",
)
retournement1(opt_cities)
ax[1].plot(
list(opt_cities[:, 0]) + [opt_cities[0, 0]],
list(opt_cities[:, 1]) + [opt_cities[0, 1]],
"ob-",
);
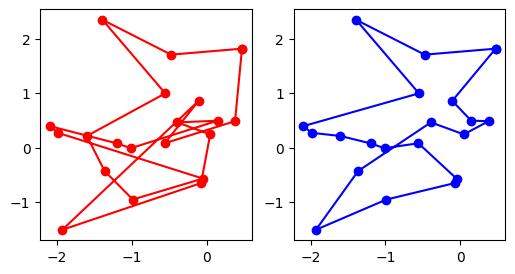
En rouge, le résultat avant la fonction retournement, en bleu après. Ce n’est pas parfait même si c’est mieux. Il faut appliquer la fonction retournement qu’il faut appeler plusieurs fois ce qu’on fait dans la même fonction.
[32]:
def retournement(cities):
d0 = distance(cities)
d_avant = d0 + 1
while d0 < d_avant:
d_avant = d0
for i in range(cities.shape[0] - 1):
for j in range(i + 1, cities.shape[0]):
cities[i : j + 1, :] = cities[i : j + 1, :][::-1]
d = distance(cities)
if d < d0:
d0 = d
else:
cities[i : j + 1, :] = cities[i : j + 1, :][::-1]
return cities
cities = numpy.array([[0, 0], [0, 2], [2, 2], [2, 0]])
retournement(cities)
[32]:
array([[0, 0],
[0, 2],
[2, 2],
[2, 0]])
[34]:
fig, ax = plt.subplots(1, 1, figsize=(3, 3))
cities = random_cities(20)
opt_cities = optimise_random(cities, 10000)[0]
retournement(opt_cities)
ax.plot(
list(opt_cities[:, 0]) + [opt_cities[0, 0]],
list(opt_cities[:, 1]) + [opt_cities[0, 1]],
"og-",
);
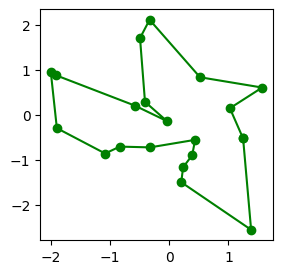
Et voilà, tout marche bien.