1A.e - Enoncé 12 décembre 2017 (1)¶

Correction du premier énoncé de l’examen du 12 décembre 2017. Celui-ci mène à l’implémentation d’un algorithme qui permet de retrouver une fonction $f$ en escalier à partir d’un ensemble de points $(X_i, f(X_i))$ .

Q1 - échantillon aléatoire¶

Générer un ensemble aléatoire de 1000 nombres $(X_i,Y_i)$ qui vérifie :

$X_i$ suit une loi uniforme sur $[0,16]$
$Y_i = \mathbb{1}_{[\sqrt{X_i}] \mod 2}$ où $[A]$ est la partie entière de $A$ .

On pourra se servir de la fonction random du module random.

[2]:

import random

X = [random.random() * 16 for i in range(0, 1000)]
Y = [int(x**0.5) % 2 for x in X]

Q1 - dessiner le nuage de points - donnée¶

Le code suivant vous est donné afin de vérifier vos réponses.

[3]:

%matplotlib inline

[4]:

import matplotlib.pyplot as plt

plt.plot(X, Y, ".")

[4]:

[<matplotlib.lines.Line2D at 0x1f893f9e518>]

../../_images/practice_exams_td_note_2018_1_5_1.png

Q2 - tri¶

Trier les points selon les $X$ .

[5]:

nuage = [(x, y) for x, y in zip(X, Y)]
nuage.sort()
nuage[:5]

[5]:

[(0.014962888038782651, 0),
 (0.020462778257442693, 0),
 (0.022310859639508962, 0),
 (0.03078728731371605, 0),
 (0.03153252863972433, 0)]

Q3 - moyenne¶

On suppose que les $Y$ sont triés selon les $X$ croissants. Calculer la moyenne des différences entre $Y$ et la moyenne $m$ des $Y$ (en valeur absolue) sur un intervalle $[i,j]$ , $j$ exclu. Ecrire une fonction def somme_diff(nuage, i, j) qui exécute ce calcul qui correspond à $\sum_{k=i}^{j-1} |Y_k - m|$ avec $m = (\sum_{k=i}^{j-1} Y_k) / (j-i)$ .

[6]:

def somme_diff(xy, i, j):
    m = sum(e[1] for e in xy[i:j]) / (j - i)
    return sum(abs(e[1] - m) for e in xy[i:j])


somme_diff(nuage, 0, 5), somme_diff(nuage, 0, len(nuage))

[6]:

(0.0, 476.2380000000092)

Q4 - distance¶

Soit $i,j$ deux entiers, on coupe l’intervalle en deux : $i,k$ et $k,j$ . On calcule la somme_diff sur ces deux intervalles, on fait la somme des différences (en valeurs absolues) de ces moyennes par rapport à la valeur sur le plus grand intervalle. On écrit la fonction def difference(nuage, i, j, k):.

[7]:

def difference(nuage, i, j, k):
    m1 = somme_diff(nuage, i, k)
    m2 = somme_diff(nuage, k, j)
    m = somme_diff(nuage, i, j)
    return abs(m1 + m2 - m)


difference(nuage, 0, len(nuage), 100)

[7]:

18.56022222223197

Q5 - fonction comme paramètre¶

Le langage Python permet de passer une fonction à une autre fonction en tant qu’argument. Un exemple :

[8]:

def fct(x, y):
    return abs(x - y)

def distance_list(list_x, list_y, f):
    return sum(f(x, y) for x, y in zip(list_x, list_y))

distance_list([0, 1], [0, 2], fct)

[8]:

Ecrire la fonction précédente en utilisant la fonction fct.

[9]:

def somme_diff(xy, i, j, f):
    m = sum(e[1] for e in xy[i:j]) / (j - i)
    # On a modifié les fonctions précédentes pour calculer
    # une fonction d'erreur "custom" ou définie par l'utilisateur.
    return sum(f(e[1], m) for e in xy[i:j])


def difference(nuage, i, j, k, f):
    m1 = somme_diff(nuage, i, k, f)
    m2 = somme_diff(nuage, k, j, f)
    m = somme_diff(nuage, i, j, f)
    return abs(m - m1) + abs(m - m2)


difference(nuage, 0, len(nuage), 100, fct)

[9]:

494.7982222222412

Q6 - optimiser¶

On veut déterminer le $i$ optimal, celui qui maximise la différence dans l’intervalle $[i,j]$ . On souhaite garder la fonction fct comme argument. Pour cela, implémenter la fonction def optimise(nuage, i, j, f):.

[10]:

def optimise(nuage, i, j, f):
    mx = -1
    ib = None
    for k in range(i + 1, j - 1):
        d = difference(nuage, i, j, k, f)
        if ib is None or d > mx:
            mx = d
            ib = k
    if ib is None:
        # Au cas où l'intervalle est vide, on retourne une coupure
        # égale à i.
        ib = i
        mx = 0
    return ib, mx


optimise(nuage, 0, len(nuage), fct)

[10]:

(565, 711.6476814159435)

[11]:

import matplotlib.pyplot as plt

x = nuage[552][0]
plt.plot(X, Y, ".")
plt.plot([x, x], [0, 1])

[11]:

[<matplotlib.lines.Line2D at 0x1f893ea57b8>]

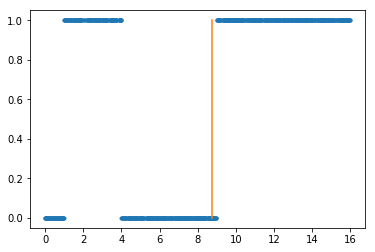
../../_images/practice_exams_td_note_2018_1_18_1.png

Le premier point de coupure trouvé (le trait orange) correspond à un des bords d’un des escaliers.

Q7 - optimisation encore¶

Recommencer sur les deux intervalles trouvés. La question était juste histoire que le résultat à la question précédente est reproductible sur d’autres intervalles.

[12]:

optimise(nuage, 0, 68, fct), optimise(nuage, 68, len(nuage), fct)

[12]:

((1, 0.0), (565, 618.0710615624871))

[13]:

import matplotlib.pyplot as plt

x = nuage[58][0]
x2 = nuage[552][0]
plt.plot(X, Y, ".")
plt.plot([x, x], [0, 1])
plt.plot([x2, x2], [0, 1])

[13]:

[<matplotlib.lines.Line2D at 0x1f8943ece80>]

../../_images/practice_exams_td_note_2018_1_22_1.png

Q8 - fonction récursive¶

Pouvez-vous imaginer une fonction récursive qui produit toutes les séparations. Ecrire la fonction def recursive(nuage, i, j, f, th=0.1):.

[14]:

def recursive(nuage, i, j, f, th=0.1):
    k, mx = optimise(nuage, i, j, f)
    if mx <= th:
        return None
    r1 = recursive(nuage, i, k, f, th=th)
    r2 = recursive(nuage, k, j, f, th=th)
    if r1 is None and r2 is None:
        return [k]
    elif r1 is None:
        return [k] + r2
    elif r2 is None:
        return r1 + [k]
    else:
        return r1 + [k] + r2


r = recursive(nuage, 0, len(nuage), fct)
r

[14]:

[68, 242, 565]

[15]:

import matplotlib.pyplot as plt

plt.plot(X, Y, ".")
for i in r:
    x = nuage[i][0]
    plt.plot([x, x], [0, 1])

../../_images/practice_exams_td_note_2018_1_25_0.png

Q9 - coût¶

Quel est le coût de la fonction optimize en fonction de la taille de l’intervalle ? Peut-on mieux faire (ce qu’on n’implémentera pas).

Tel qu’il est implémenté, le coût est en $O(n^2)$ , le coût peut être linéaire en triant les éléments dans l’ordre croissant, ce qui a été fait, ou $n\ln n$ si on inclut le coût du tri bien qu’on ne le fasse qu’une fois. Voyons plus en détail comment se débarrasser du coût en $O(n^2)$ . Tout d’abord la version actuelle.

[16]:

def somme_diff_abs(xy, i, j):
    m = sum(e[1] for e in xy[i:j]) / (j - i)
    return sum(abs(e[1] - m) for e in xy[i:j])


def difference_abs(nuage, i, j, k):
    m1 = somme_diff_abs(nuage, i, k)
    m2 = somme_diff_abs(nuage, k, j)
    m = somme_diff_abs(nuage, i, j)
    return abs(m1 + m2 - m)


def optimise_abs(nuage, i, j):
    mx = -1
    ib = None
    for k in range(i + 1, j - 1):
        d = difference_abs(nuage, i, j, k)
        if ib is None or d > mx:
            mx = d
            ib = k
    if ib is None:
        ib = i
        mx = 0
    return ib, mx


%timeit optimise_abs(nuage, 0, len(nuage))

503 ms ± 21.1 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)

L’instruction suivante permet de voir où le programme passe la majeure partie de son temps.

[17]:

# %prun optimise_abs(nuage, 0, len(nuage))

La fonction sum cache une boucle, avec la boucle for dans la fonction optimise, cela explique le coût en $O(n^2)$ . Le fait qu’à chaque itération, on passe une observation d’un côté à l’autre de la coupure puis on recalcule les moyennes… Il y a deux façons d’optimiser ce calcul selon qu’on tient compte du fait que les valeurs de $Y$ sont binaires ou non.

Dans le premier cas, il suffit de compter les valeurs 0 ou 1 de part et d’autres de la coupure (histogrammes) pour calculer la moyenne. Lorsque $k$ varie, il suffit de mettre à jour les histogrammes en déduisant et en ajoutant le $Y_k$ aux bons endroits.

[18]:

def histogramme_y(xy, i, j):
    d = [0, 0]
    for x, y in xy[i:j]:
        d[y] += 1
    return d


def somme_diff_histogramme(d):
    m = d[1] * 1.0 / (d[0] + d[1])
    return (1 - m) * d[1] + m * d[0]


def optimise_rapide(nuage, i, j):
    # On calcule les histogrammes.
    d1 = histogramme_y(nuage, i, i + 1)
    d2 = histogramme_y(nuage, i + 1, j)
    d = d1.copy()
    d[0] += d2[0]
    d[1] += d2[1]

    m = somme_diff_histogramme(d)
    m1 = somme_diff_histogramme(d1)
    m2 = somme_diff_histogramme(d2)
    mx = -1
    ib = None
    for k in range(i + 1, j - 1):
        d = abs(m1 + m2 - m)
        if ib is None or d > mx:
            mx = d
            ib = k
        # On met à jour les histogrammes. On ajoute d'un côté, on retranche de l'autre.
        y = nuage[k][1]
        d1[y] += 1
        d2[y] -= 1
        m1 = somme_diff_histogramme(d1)
        m2 = somme_diff_histogramme(d2)
    if ib is None:
        ib = i
        mx = 0
    return ib, mx


# On vérifie qu'on obtient les mêmes résultats.
optimise_rapide(nuage, 0, len(nuage)), optimise_abs(nuage, 0, len(nuage))

[18]:

((565, 235.4096814159292), (565, 235.40968141593424))

C’est carrément plus rapide et cela marche pour toute fonction fct.

[19]:

%timeit optimise_rapide(nuage, 0, len(nuage))

1.63 ms ± 150 µs per loop (mean ± std. dev. of 7 runs, 1000 loops each)

Si on ne suppose pas que les $Y_i$ sont binaires et qu’ils sont quelconques, les histogrammes contiendront plus de deux éléments. Dans ce cas, il faut conserver deux tableaux triés des $Y_i$ , de part et d’autres de la coupure. Lorsqu’on bouge la coupure $k$ , cela revient à déplacer $Y_k$ d’un tableau à l’autre ce qui se fera par recherche dichotomique donc en $O(\ln n)$ . La mise à jour de la moyenne des valeurs absolues est immédiate si la fonction fct=abs(x-y) et pas forcément immédiate dans le cas général. Lorsque c’est une valeur absolue, il faut utiliser quelques résultats sur la régression quantile.

Q10 - autre nuage de points¶

Comment l’algorithme se comporte-t-il lorsque tous les points sont distincts ?

[20]:

import random

X2 = list(range(10))
Y2 = X2

[21]:

import matplotlib.pyplot as plt

plt.plot(X2, Y2, ".")

[21]:

[<matplotlib.lines.Line2D at 0x1f8944d3ba8>]

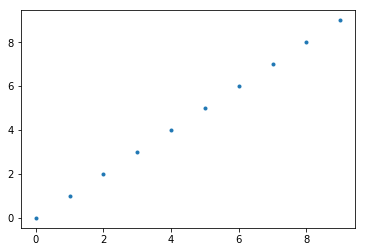
../../_images/practice_exams_td_note_2018_1_38_1.png

[22]:

nuage2 = [(x, y) for x, y in zip(X2, Y2)]
nuage2.sort()

[23]:

r = recursive(nuage2, 0, len(nuage2), fct)
len(r), r

[23]:

(5, [2, 3, 5, 7, 8])

[24]:

import matplotlib.pyplot as plt

plt.plot(X2, Y2, ".")
for i in r:
    x = nuage2[i][0]
    plt.plot([x, x], [0, 10])

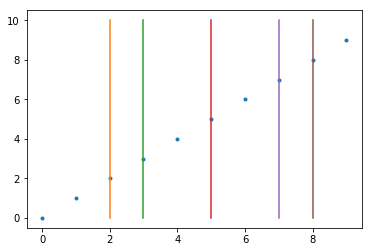
../../_images/practice_exams_td_note_2018_1_41_0.png

La fonction va placer un point dans chaque intervalle, il y aura quasiment autant de points de coupures que de points. Presque autant car l’implémentation a quelques effets de bords comme la boucle for k in range(i+1,j-1): qui ne considère pas les extrémités d’un intervalle comme de potentiels points de coupures.

[25]:

Notebook on github