La sous-séquence de plus grande somme¶

Ce problème est connu sur le nom de Maximum subarray problem. Notion abordée : programmation dynamique.

[1]:

%matplotlib inline

Enoncé¶

On suppose qu’on a une liste $L=( l_1, l_2, ..., l_n)$ . On souhaite trouver la sous-séquence de plus grande somme. En d’autres termes, on veut trouver $(i^*,j^*)$ tels que :

$\sum_{k=i^*}^{j^*} l_k = \max_{i,j} \sum_{k=i}^{j} l_k$

Solution naïve¶

La première solution consiste à calculer les sommes de toutes les sous-séquences et de garder les $i,j$ qui ont permis d’obtenir la meilleure sous-séquence. On divise le programme en deux fonctions :

somme_partielle : calcule la somme de la sous-séquence l[i:j] (coût de la fonction : $O(n)$ )
plus_grande_sous_liste : passe en revue toutes les sous-séquences et retourne la meilleure (coût de la fonction $O(n^2)$ )

Le coût de cet algorithme est en $O(n^3)$ .

[2]:

def somme_partielle(li, i, j):
    r = 0
    for a in range(i, j):
        r += li[a]
    return r
    # on pourrait juste écrire
    # return sum(li[i:j])


def plus_grande_sous_liste(li):
    meilleur = min(li)  # ligne A
    im, jm = -1, -1
    for i in range(0, len(li)):
        for j in range(i + 1, len(li) + 1):  # ne pas oublier +1 car sinon
            # le dernier élément n'est jamais pris en compte
            s = somme_partielle(li, i, j)
            if s > meilleur:
                meilleur = s
                im, jm = i, j
    return li[im:jm]


# si li ne contient que des valeurs positives, la solution est évidemment la liste entière
# c'est pourquoi il faut tester cette fonction avec des valeurs négatives
li = [4, -6, 7, -1, 8, -50, 3]
m = plus_grande_sous_liste(li)
m

[2]:

[7, -1, 8]

La ligne A contient l’instruction meilleur = min(li). Pour une liste où tous les nombres sont négatifs, la meilleure sous-liste est constitué du plus petit élément de la liste. Remplacer cette instruction par meilleur = 0 a pour conséquence de retourner une liste vide dans ce cas précis.

$cout(n) = \sum_{i=0}^n \sum_{j=i+1}^n j-i = \sum_{i=0}^n \sum_{j=0}^i j = \sum_{i=0}^n \frac{i(i+1)}{2} \sim O(n^3)$

Solution plus rapide¶

Il est possible de modifier cette fonction de telle sorte que le coût soit en $O(n^2)$ car on évite la répétition de certains calculs lors du calcul de la somme des sous-séquences. On peut écrire :

$\sum_{k=i}^{j+1} l_k = l_j + \sum_{k=i}^{j} l_k$

Dans la seconde boucle, il suffit d’ajouter l’élément li[j] à la somme précédente.

[3]:

def plus_grande_sous_liste_n2(li):
    meilleur = 0
    im, jm = -1, -1
    for i in range(0, len(li)):
        s = 0
        for j in range(i, len(li)):
            s += li[j]
            if s > meilleur:
                meilleur = s
                im, jm = i, j + 1
    return li[im:jm]


li = [4, -6, 7, -1, 8, -50, 3]
m = plus_grande_sous_liste_n2(li)
print(m)

li = [1, 2, 3, 4, 5, -98, 78, 9, 7, 7]
m = plus_grande_sous_liste_n2(li)
print(m)

li = [0, 2, 4, -7, -2, 7, -1, 8, -10, 3]
m = plus_grande_sous_liste_n2(li)
m

[7, -1, 8]
[78, 9, 7, 7]

[3]:

[7, -1, 8]

Solution dichotomique¶

Il existe une dernière version plus rapide encore. Si on considère la liste $L=(l_1, ..., l_n)$ dont on cherche à extraire la sous-séquence de somme maximale. Supposons que $l_a$ appartienne à cette sous-séquence. On construit la fonction suivante :

$f(a,k) =\left \{ \begin{array}{ll} \sum_{i=a}^{k} l_i &si \; k > a \\ \sum_{i=k}^{a} l_i &si \; k < a \end{array} \right .$

On cherche alors les valeurs $k_1$ et $k_2$ telles que :

$\begin{array}{rcl} f(a,k_1) &=& \max_{k<a} f(a,k) \\ f(a,k_2) &=& \max_{k>a} f(a,k) \end{array}$

La sous-séquence de somme maximale cherchée est $[k_1,k_2]$ avec $a$ dans cet intervalle et le coût de cette recherche est en $O(n)$ . Mais ceci n’est vrai que si on sait que $l_a$ appartient à la sous-séquence de somme maximale.

Autre considération : pour deux listes $l_1$ et $l_2$ , la séquence maximale de la réunion des deux appartient soit à l’une, soit à l’autre, soit elle inclut le point de jonction.

Ces deux idées mises bout à bout donne l’algorithme suivant construit de façon récursive. On coupe la liste en deux parties de longueur égale :

On calcule la meilleure séquence sur la première sous-séquence.
On calcule la meilleure séquence sur la seconde sous-séquence.
On calcule la meilleure séquence en suppose que l’élément du milieu appartient à cette séquence.

La meilleure séquence est nécessairement l’une des trois.

[4]:

def plus_grande_sous_liste_nlnn2_r(li, i, j):
    if i == j:
        return 0
    elif i + 1 == j:
        return li[i], i, i + 1

    milieu = (i + j) // 2

    # on coupe le problème deux
    ma, ia, ja = plus_grande_sous_liste_nlnn2_r(li, i, milieu)
    mb, ib, jb = plus_grande_sous_liste_nlnn2_r(li, milieu, j)

    # pour aller encore plus vite dans un cas précis
    if ja == ib:
        total = ma + mb
        im, jm = ia, jb
    else:
        # on étudie la jonction
        im, jm = milieu, milieu + 1
        meilleur = li[milieu]
        s = meilleur
        for k in range(milieu + 1, j):
            s += li[k]
            if s > meilleur:
                meilleur = s
                jm = k + 1

        total = meilleur
        meilleur = li[milieu]
        s = meilleur
        for k in range(milieu - 1, i - 1, -1):
            s += li[k]
            if s > meilleur:
                meilleur = s
                im = k

        total += meilleur - li[milieu]

    if ma >= max(mb, total):
        return ma, ia, ja
    elif mb >= max(ma, total):
        return mb, ib, jb
    else:
        return total, im, jm


def plus_grande_sous_liste_nlnn2(li):
    m, i, j = plus_grande_sous_liste_nlnn2_r(li, 0, len(li))
    return li[i:j]


li = [4, -6, 7, -1, 8, -50, 3]
m = plus_grande_sous_liste_nlnn2(li)
print(m)

li = [1, 2, 3, 4, 5, -98, 78, 9, 7, 7]
m = plus_grande_sous_liste_nlnn2(li)
print(m)

li = [0, 2, 4, -7, -2, 7, -1, 8, -10, 3]
m = plus_grande_sous_liste_nlnn2(li)
m

[7, -1, 8]
[78, 9, 7, 7]

[4]:

[7, -1, 8]

Le coût de cette fonction est au pire en $O(n \ln n)$ . A chaque itération, on effectue trois calculs :

meilleure séquence à droite : $f(n/2)$
meilleure séquence à gauche : $f(n/2)$
meilleure séquence incluant $a$ : $n$

Le coût de l’iteration $n$ est $f(n)=n + 2f(n/2)$ avec $f(1)=0$ . On calcule les premières termes :

[5]:

cout = lambda n: 0 if n == 1 else n + 2 * cout(n // 2)
for i in range(1, 10):
    print("f({0})={1} --> f({0})/{0} = {2}".format(2**i, cout(2**i), cout(2**i) / 2**i))

f(2)=2 --> f(2)/2 = 1.0
f(4)=8 --> f(4)/4 = 2.0
f(8)=24 --> f(8)/8 = 3.0
f(16)=64 --> f(16)/16 = 4.0
f(32)=160 --> f(32)/32 = 5.0
f(64)=384 --> f(64)/64 = 6.0
f(128)=896 --> f(128)/128 = 7.0
f(256)=2048 --> f(256)/256 = 8.0
f(512)=4608 --> f(512)/512 = 9.0

On suppose que $f(2^n)=n2^n \Leftrightarrow f(n) = n \ln_2 n$ . Il suffit de vérifier cela avec la récurrence :

$\begin{array}{rcl} f(n) &=& n + 2f(\frac{n}{2}) = n + 2 \frac{n}{2} \ln_2(\frac{n}{2}) \\ &=& n + n \ln_2(n) - n\ln_2(2) = n + n\ln_2(n) - n = n\ln_2 n\end{array}$

C’est le coût d’une itération. Comme à chaque itération on coupe le problème en deux, le coût total de l’algorithme est :

$\begin{array}{rcl} C(2^n) &=& f(2^n) + 2f(2^{n-1}) + 4f(2^{n-2}) + ... + 2^{n-1}f(2) = \sum_{k=1}^{n} 2^{n-k} f(2^k) \\ &=& \sum_{k=1}^n 2^{n-k} 2^k k = \sum_{k=1}^n 2^n k = 2^{n-1}n(n-1) \leqslant 2^{n-1} n^2 \end{array}$

Par conséquent, le coût est en $C(n) \sim O(n \ln^2 n)$ .

Solution linéaire¶

La dernière solution est la plus rapide. Elle consiste à parcourir la liste dans le sens croissant des indices et à construire la série cumulée.

[6]:

import matplotlib.pyplot as plt

li = [0, 2, 4, -7, -2, 7, -1, 8, -10, 3]
cumul = [li[0]]
for i in li[1:]:
    cumul.append(cumul[-1] + i)
cumul2 = [li[0]]
for i in li[1:]:
    cumul2.append(max(cumul2[-1] + i, 0))
plt.plot(cumul, label="cumul")
plt.plot(cumul2, label="cumul2")
plt.plot([0 for c in cumul])
plt.legend()
plt.title("somme cumulée");

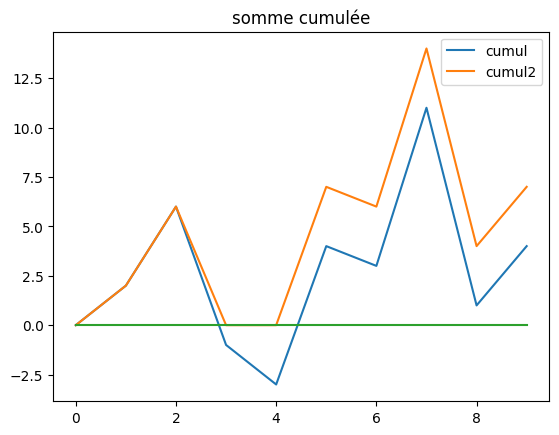
../../_images/practice_algo-base_exercice_plus_grande_somme_14_0.png

La courbe devient négative au quatrième nombre. L’astuce consiste à dire qu’on peut traiter les deux ensembles séparément et que la meilleure sous-séquence n’inclura pas ce nombre en quatrième position. Si on cherche la meilleure sous-séquence se terminant à la position $i$ , il suffit juste de revenir en arrière et de trouver le minimum de la courbe cumulée avant la position $i$ . Pour $i=5$ , le point le plus bas qui précède est le point $k=3$ . Au point $i=3$ , on sait qu’il n’existe pas de sous-séquence positive précédent $i=3$ .

On découpe la courbe en segments $[[i,j]]$ vérifiant $l_{i-1} < 0 \leqslant l_i$ et $\sum_{k=1}^{j} l_k < 0$ et $l_{j+1} \geqslant 0$ .

[7]:

from IPython.core.display import Image

Image("sommemax.png")

[7]:

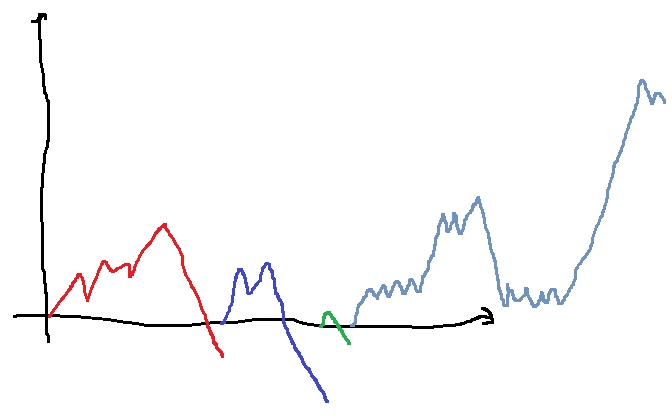
../../_images/practice_algo-base_exercice_plus_grande_somme_16_0.png

On parcourt la série cumulée. A chaque fois qu’on passe sous zéro, au premier nombre positif suivant, on redémarre à zéro. La sous-séquence de somme maximale est forcément dans un de ces tronçons, elle a pour point de départ le premier élément et pour point d’arrivée le maximum obtenu sur le tronçon en question : pour chaque point $x,Cumul2(x)$ d’un tronçon, le minimum de la courbe cumulée précédent $x$ est nécessairement le premier élément du tronçon.

[8]:

def plus_grande_sous_liste_n(li):
    meilleur = [None for i in li]
    somme = [None for i in li]
    best = None

    for i, el in enumerate(li):
        if el >= 0:
            if i > 0:
                somme[i] = max(somme[i - 1], 0) + el
                meilleur[i] = meilleur[i - 1] if somme[i - 1] >= 0 else i
            else:
                somme[i] = el
                meilleur[i] = i
            if best is None or somme[i] > somme[best]:
                best = i
        else:
            somme[i] = (somme[i - 1] + el) if i > 0 else el
            if somme[i] >= 0:
                meilleur[i] = meilleur[i - 1]

    i, j = meilleur[best], best + 1
    return li[i:j]


li = [4, -6, 7, -1, 8, -10, 3]
m = plus_grande_sous_liste_n(li)
print(m)  # affiche [7, -1, 8]

li = [1, 2, 3, 4, 5, -98, 78, 9, 7, 7]
m = plus_grande_sous_liste_n(li)
print(m)

li = [0, 2, 4, -7, -2, 7, -1, 8, -10, 3]
m = plus_grande_sous_liste_n(li)
m

[7, -1, 8]
[78, 9, 7, 7]

[8]:

[7, -1, 8]

Comparaison des temps de calcul¶

On effectue cela sur une liste de nombres aléatoire négatifs et positifs.

[9]:

import random

li100 = [random.randint(-10, 50) for i in range(0, 100)]

Coût en $O(n^3)$ :

[10]:

%timeit plus_grande_sous_liste(li100)

15.6 ms ± 1.19 ms per loop (mean ± std. dev. of 7 runs, 100 loops each)

Coût en $O(n^2)$ :

[11]:

%timeit plus_grande_sous_liste_n2(li100)

565 µs ± 33.7 µs per loop (mean ± std. dev. of 7 runs, 1,000 loops each)

Coût en $O(n \ln^2 n)$ :

[12]:

%timeit plus_grande_sous_liste_nlnn2(li100)

134 µs ± 12.9 µs per loop (mean ± std. dev. of 7 runs, 10,000 loops each)

Coût en $O(n)$ :

[13]:

%timeit plus_grande_sous_liste_n(li100)

70.9 µs ± 3.32 µs per loop (mean ± std. dev. of 7 runs, 10,000 loops each)

Application¶

Le drawdown est un indicateur de performance pour les systèmes de trading. Il mesure la perte maximale enregistrée sur une période. En d’autres, il correspond à la sous-séquence de somme minimale. On vient de montrer qu’il n’est pas plus long à calculer qu’une moyenne.

[ ]:

Notebook on github