Réflexions autour du voyage de commerce (TSP)

Le problème du voyageur de commerce consiste à trouver le plus court chemin passant par toutes les villes. On parle aussi de circuit hamiltonien qui consiste à trouver le plus court chemin passant par tous les noeuds d’un graphe. Ce programme explore quelques solutions approchées et intuitives.

Ce problème est NP-complet à savoir qu’il n’existe pas d’algorithme qui permette de trouver la solution avec un coût polynômial. C’est aussi un problème différent du plus court chemin dans un graphe qui consiste à trouver le plus court chemin reliant deux noeuds d’un graphe (mais pas forcément tous les noeuds de ce graphe).

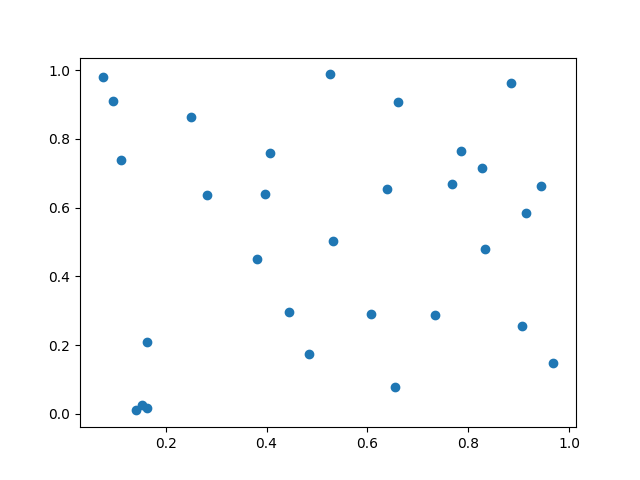
Des villes tirées au hasard

import random
import matplotlib.pyplot as plt

n = 30
x = [random.random() for _ in range(n)]
y = [random.random() for _ in range(n)]

plt.plot(x, y, "o")

[<matplotlib.lines.Line2D object at 0x7267dfc48200>]

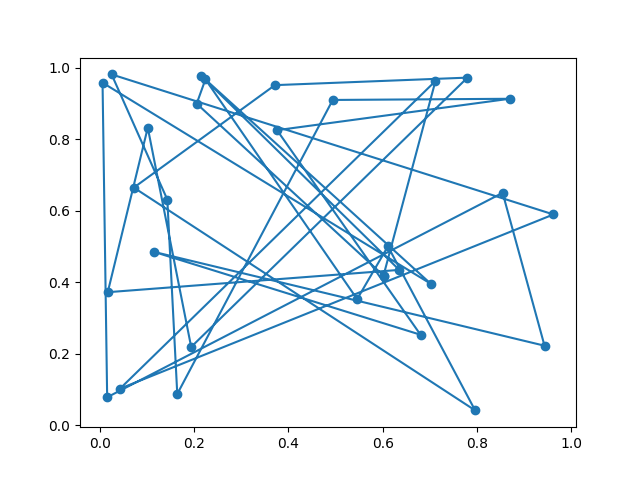
Un parcours aléatoire de tous les noeuds de graphe donnera quelque chose de très éloigné de la solution optimale :

plt.plot([*x, x[0]], [*y, y[0]], "o-")

[<matplotlib.lines.Line2D object at 0x7267dfc72570>]

Croisements

La première constation est que le chemin ne peut pas être optimal car des arcs se croisent. On en déduit qu’une façon d’améliorer ce chemin est de décroiser certaines parties. On peut par exemple choisir deux points au hasard, retourner la partie du chemin au milieu de ces deux points et voir si la longueur du chemin s’en trouve diminuée. On peut également parcourir toutes les paires de noeuds possibles. C’est ce qui est implémenté ci-dessous.

def longueur(x, y, ordre):
    i = ordre[-1]
    x0, y0 = x[i], y[i]
    d = 0
    for o in ordre:
        x1, y1 = x[o], y[o]
        d += (x0 - x1) ** 2 + (y0 - y1) ** 2
        x0, y0 = x1, y1
    return d


ordre = list(range(len(x)))
print("longueur initiale", longueur(x, y, ordre))

longueur initiale 10.30408999030914

Permutations.

def permutation(x, y, ordre):
    d = longueur(x, y, ordre)
    d0 = d + 1
    it = 1
    while d < d0:
        it += 1
        print("iteration", it, "d=", d)
        d0 = d
        for i in range(len(ordre) - 1):
            for j in range(i + 2, len(ordre)):
                r = ordre[i:j].copy()
                r.reverse()
                ordre2 = ordre[:i] + r + ordre[j:]
                t = longueur(x, y, ordre2)
                if t < d:
                    d = t
                    ordre = ordre2
    return ordre


ordre = permutation(x, y, list(range(len(x))))
print("longueur min", longueur(x, y, ordre))
xo = [x[o] for o in [*ordre, ordre[0]]]
yo = [y[o] for o in [*ordre, ordre[0]]]
plt.plot(xo, yo, "o-")

iteration 2 d= 10.30408999030914
iteration 3 d= 1.7332618169352088
iteration 4 d= 1.2415486996123526
iteration 5 d= 1.1482116251492283
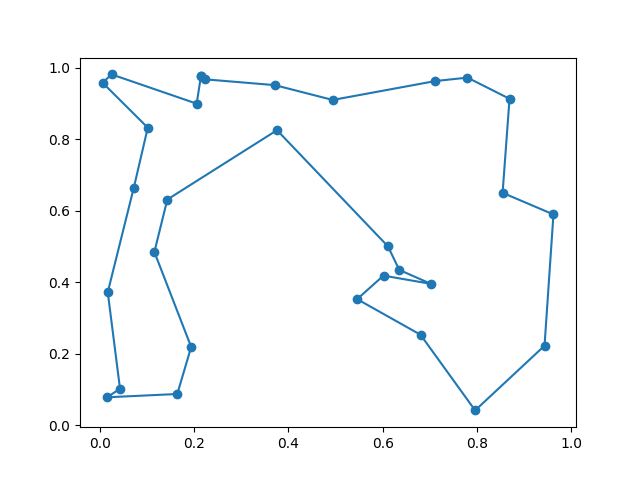
longueur min 1.1482116251492283

[<matplotlib.lines.Line2D object at 0x7267dfba6810>]

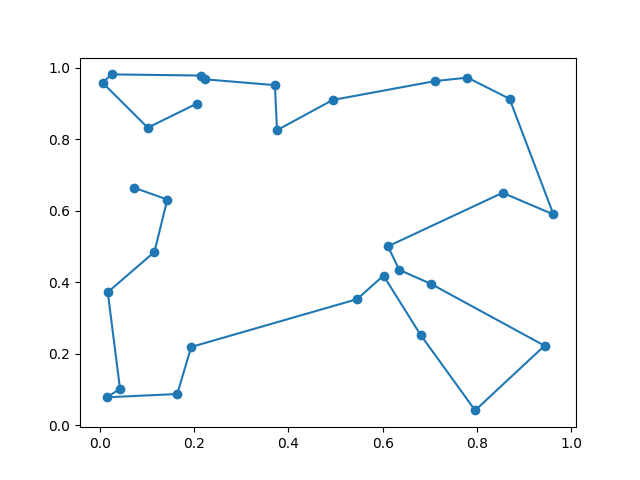
Voilà qui est mieux. Maintenant, supposons que nous faisons une erreur lors du calcul de la distance : nous oublions le dernier arc qui boucle le chemin du dernier noeud au premier.

def longueur(x, y, ordre):
    # on change cette fonction
    d = 0
    for i in range(1, len(ordre)):
        n = ordre[i - 1]
        o = ordre[i]
        x0, y0 = x[n], y[n]
        x1, y1 = x[o], y[o]
        d += (x0 - x1) ** 2 + (y0 - y1) ** 2
    return d


ordre = list(range(len(x)))
print("longueur initiale", longueur(x, y, ordre))

longueur initiale 10.051165479082176

Et graphiquement.

ordre = permutation(x, y, list(range(len(x))))
print("longueur min", longueur(x, y, ordre))
xo = [x[o] for o in ordre]
yo = [y[o] for o in ordre]
plt.plot(xo, yo, "o-")

iteration 2 d= 10.051165479082176
iteration 3 d= 1.577553415973726
iteration 4 d= 1.1960488579751223
iteration 5 d= 1.0533402775396394
longueur min 1.0533402775396394

[<matplotlib.lines.Line2D object at 0x7267dfc70920>]

Noeud de départ constant

Jusque ici, tout concorde. Le chemin est plus court en ce sens qu’il oublie délibérément l’arc de bouclage que l’algorithme a tendance à choisir grand. Pour gagner du temps de calcul, un développeur se dit que le noeud de départ peut être constant. Après tout, le chemin est une boucle, elle passera toujours par le premier noeud. Qu’il soit en première position ne change rien et puis inverser une moitié, c’est équivalent à inverser l’autre moitié. On fait donc juste une modification :

def longueur(x, y, ordre):
    i = ordre[-1]
    x0, y0 = x[i], y[i]
    d = 0
    for o in ordre:
        x1, y1 = x[o], y[o]
        d += (x0 - x1) ** 2 + (y0 - y1) ** 2
        x0, y0 = x1, y1
    return d


ordre = list(range(len(x)))
print("longueur initiale", longueur(x, y, ordre))


def permutation(x, y, ordre):
    d = longueur(x, y, ordre)
    d0 = d + 1
    it = 1
    while d < d0:
        it += 1
        print("iteration", it, "d=", d, "ordre[0]", ordre[0])
        d0 = d
        for i in range(
            1, len(ordre) - 1
        ):  # on part de 1 et plus de 0, on est sûr que le premier noeud ne bouge pas
            for j in range(i + 2, len(ordre)):
                r = ordre[i:j].copy()
                r.reverse()
                ordre2 = ordre[:i] + r + ordre[j:]
                t = longueur(x, y, ordre2)
                if t < d:
                    d = t
                    ordre = ordre2
    return ordre


ordre = permutation(x, y, list(range(len(x))))
print("longueur min", longueur(x, y, ordre))
xo = [x[o] for o in [*ordre, ordre[0]]]
yo = [y[o] for o in [*ordre, ordre[0]]]
plt.plot(xo, yo, "o-")
plt.text(xo[0], yo[0], "0", color="r", weight="bold", size="x-large")
plt.text(xo[-2], yo[-2], "N-1", color="r", weight="bold", size="x-large")

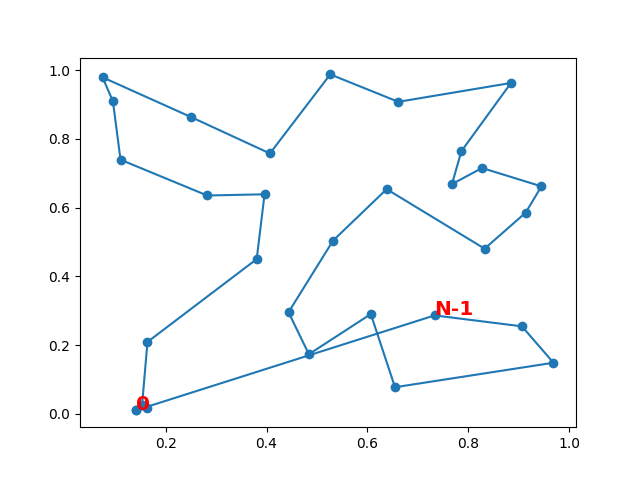
longueur initiale 10.30408999030914
iteration 2 d= 10.30408999030914 ordre[0] 0
iteration 3 d= 1.6329815361151536 ordre[0] 0
iteration 4 d= 1.4496523205497671 ordre[0] 0
iteration 5 d= 1.3748064953628787 ordre[0] 0
longueur min 1.3748064953628787

Text(0.4956274975376094, 0.023022278257650686, 'N-1')

Le résultat attendu n’est pas celui qu’on observe. Est-ce une erreur d’implémentation ou une erreur de raisonnement ? J’étais pourtant sûr que mon raisonnement était correct et j’aurais tort d’en douter. C’est une erreur d’implémentation. Lorsqu’on``for j in range(i+2,len(ordre)):`` et r = ordre[i:j].copy(), on écrit que j va de i+2 inclus à len(ordre) exclu. Puis lorsqu’on écrit ordre[i:j], l’indice j est exclu ! Autrement dit, dans cette implémentation, le premier noeud et le dernier noeud ne bougeront jamais ! On s’empresse de corriger cela.

ordre = list(range(len(x)))
print("longueur initiale", longueur(x, y, ordre))


def permutation(x, y, ordre):
    d = longueur(x, y, ordre)
    d0 = d + 1
    it = 1
    while d < d0:
        it += 1
        print("iteration", it, "d=", d, "ordre[0]", ordre[0])
        d0 = d
        for i in range(
            1, len(ordre) - 1
        ):  # on part de 1 et plus de 0, on est sûr que le premier noeud ne bouge pas
            for j in range(i + 2, len(ordre) + 1):  # correction !
                r = ordre[i:j].copy()
                r.reverse()
                ordre2 = ordre[:i] + r + ordre[j:]
                t = longueur(x, y, ordre2)
                if t < d:
                    d = t
                    ordre = ordre2
    return ordre


ordre = permutation(x, y, list(range(len(x))))
print("longueur min", longueur(x, y, ordre))
xo = [x[o] for o in [*ordre, ordre[0]]]
yo = [y[o] for o in [*ordre, ordre[0]]]
plt.plot(xo, yo, "o-")
plt.text(xo[0], yo[0], "0", color="r", weight="bold", size="x-large")
plt.text(xo[-2], yo[-2], "N-1", color="r", weight="bold", size="x-large")

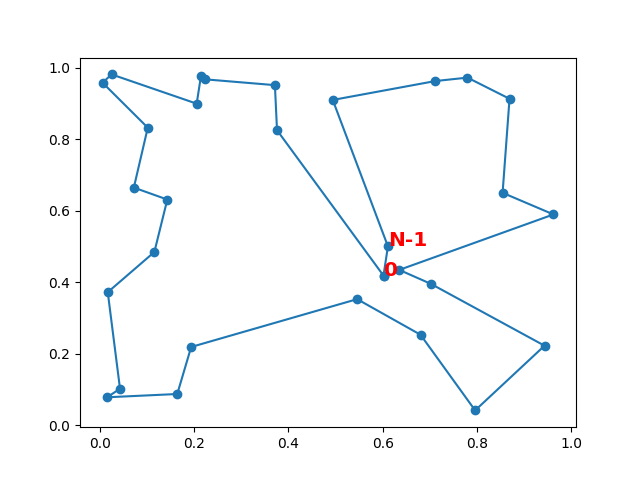
longueur initiale 10.30408999030914
iteration 2 d= 10.30408999030914 ordre[0] 0
iteration 3 d= 1.9879903839893633 ordre[0] 0
iteration 4 d= 1.0633623877373592 ordre[0] 0
iteration 5 d= 1.063362387737359 ordre[0] 0
longueur min 1.063362387737359

Text(0.6804311442916652, 0.6498690413854012, 'N-1')

Pas parfait mais conforme à nos attentes (les miennes en tout cas) ! Soit dit en passant, la première version de l’algorithme laissait déjà le dernier noeud inchangé.

Un peu d’aléatoire en plus

La solution n’est pas parfaite en ce sens que visuellement, on voit que certaines parties du chemin pourraient être facilement améliorées. Mais si la solution était parfaite en toute circonstance, nous aurions trouvé un algorithme à temps polynômial ce qui est impossible. Dans notre cas, l’algorithme produit toujours la même solution car il parcourt les noeuds toujours dans le même sens. Un peu d’aléa devrait l’aider à trouver de meilleures solutions après quelques essais.

# In[8]:


ordre = list(range(len(x)))
print("longueur initiale", longueur(x, y, ordre))


def permutation_rnd(x, y, ordre):
    d = longueur(x, y, ordre)
    d0 = d + 1
    it = 1
    while d < d0:
        it += 1
        print("iteration", it, "d=", d, "ordre[0]", ordre[0])
        d0 = d
        for i in range(1, len(ordre) - 1):
            for _j in range(i + 2, len(ordre) + 1):
                ik = random.randint(1, len(ordre) - 1)
                il = random.randint(ik + 1, len(ordre))
                r = ordre[ik:il].copy()
                r.reverse()
                ordre2 = ordre[:ik] + r + ordre[il:]
                t = longueur(x, y, ordre2)
                if t < d:
                    d = t
                    ordre = ordre2
    return ordre


ordre = permutation_rnd(x, y, list(range(len(x))))
print("longueur min", longueur(x, y, ordre))
xo = [x[o] for o in [*ordre, ordre[0]]]
yo = [y[o] for o in [*ordre, ordre[0]]]
plt.plot(xo, yo, "o-")
plt.text(xo[0], yo[0], "0", color="r", weight="bold", size="x-large")
plt.text(xo[-2], yo[-2], "N-1", color="r", weight="bold", size="x-large")

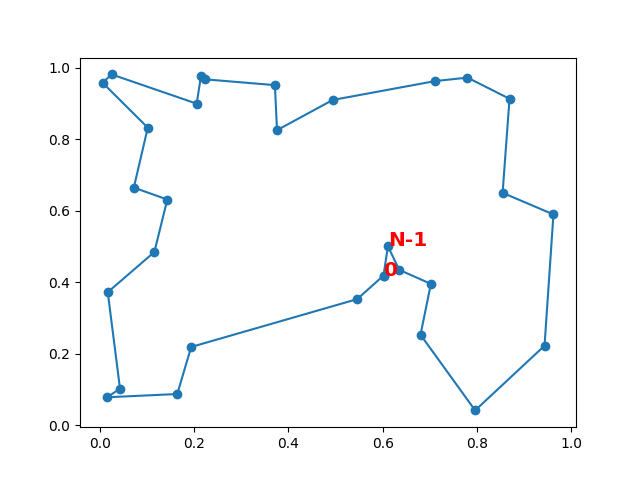
longueur initiale 10.30408999030914
iteration 2 d= 10.30408999030914 ordre[0] 0
iteration 3 d= 1.772812161964937 ordre[0] 0
iteration 4 d= 1.4764997214835205 ordre[0] 0
iteration 5 d= 1.321234753945295 ordre[0] 0
iteration 6 d= 1.0647567400724298 ordre[0] 0
longueur min 1.0647567400724298

Text(0.9109370516066633, 0.36696425312789427, 'N-1')

Ca a l’air de marcher un peu mieux mais quelques aberrations car l’aléatoire n’est pas un parcours systématique de toutes les pairs. Par conséquent, il peut rester des croisements :

ordre = permutation_rnd(x, y, list(range(len(x))))
print("longueur min", longueur(x, y, ordre))
xo = [x[o] for o in [*ordre, ordre[0]]]
yo = [y[o] for o in [*ordre, ordre[0]]]
plt.plot(xo, yo, "o-")
plt.text(xo[0], yo[0], "0", color="r", weight="bold", size="x-large")
plt.text(xo[-2], yo[-2], "N-1", color="r", weight="bold", size="x-large")

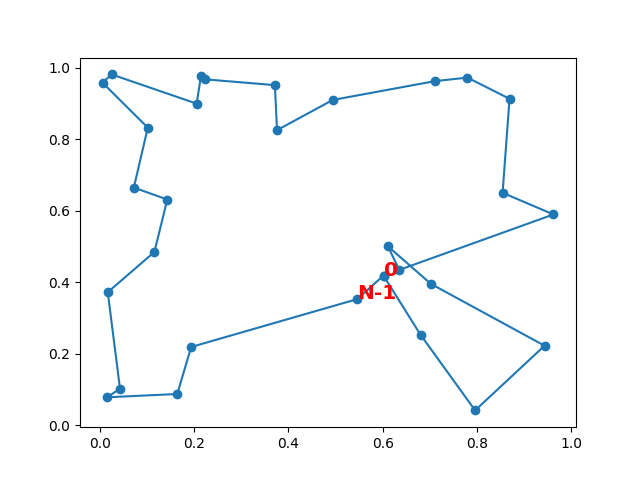
iteration 2 d= 10.30408999030914 ordre[0] 0
iteration 3 d= 1.8514436107134233 ordre[0] 0
iteration 4 d= 1.4961621716307751 ordre[0] 0
iteration 5 d= 1.2526826250358791 ordre[0] 0
iteration 6 d= 1.2526826250358787 ordre[0] 0
longueur min 1.2526826250358787

Text(0.8271991721743198, 0.7253945008811771, 'N-1')

Pour éviter cela, on peut imposer un nombre d’itérations minimum et recommencer plusieurs à partir d’ordre initiaux aléatoires :

def permutation_rnd(x, y, ordre, miniter):
    d = longueur(x, y, ordre)
    d0 = d + 1
    it = 1
    while d < d0 or it < miniter:
        it += 1
        d0 = d
        for i in range(1, len(ordre) - 1):
            for _j in range(i + 2, len(ordre) + 1):
                ik = random.randint(1, len(ordre) - 1)
                il = random.randint(ik + 1, len(ordre))
                r = ordre[ik:il].copy()
                r.reverse()
                ordre2 = ordre[:ik] + r + ordre[il:]
                t = longueur(x, y, ordre2)
                if t < d:
                    d = t
                    ordre = ordre2
    return ordre


def n_permutation(x, y, miniter):
    ordre = list(range(len(x)))
    bordre = ordre.copy()
    d0 = longueur(x, y, ordre)
    for i in range(20):
        print("iteration", i, "d=", d0)
        random.shuffle(ordre)
        ordre = permutation_rnd(x, y, ordre, 20)
        d = longueur(x, y, ordre)
        if d < d0:
            d0 = d
            bordre = ordre.copy()
    return bordre

La distance initiale.

ordre = list(range(len(x)))
print("longueur initiale", longueur(x, y, ordre))

longueur initiale 10.30408999030914

La longueur obtenue.

ordre = n_permutation(x, y, 20)
print("longueur min", longueur(x, y, ordre))
xo = [x[o] for o in [*ordre, ordre[0]]]
yo = [y[o] for o in [*ordre, ordre[0]]]
plt.plot(xo, yo, "o-")
plt.text(xo[0], yo[0], "0", color="r", weight="bold", size="x-large")
plt.text(xo[-2], yo[-2], "N-1", color="r", weight="bold", size="x-large")


# C'est mieux.

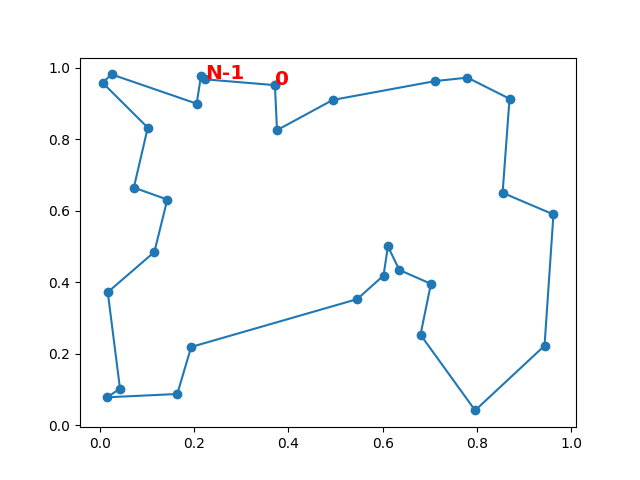
iteration 0 d= 10.30408999030914
iteration 1 d= 0.9205631171121537
iteration 2 d= 0.9205631171121537
iteration 3 d= 0.9063759511026203
iteration 4 d= 0.9063759511026203
iteration 5 d= 0.9063759511026203
iteration 6 d= 0.9063759511026203
iteration 7 d= 0.9063759511026203
iteration 8 d= 0.9063759511026203
iteration 9 d= 0.9063759511026203
iteration 10 d= 0.9063759511026203
iteration 11 d= 0.9063759511026203
iteration 12 d= 0.9063759511026203
iteration 13 d= 0.9063759511026203
iteration 14 d= 0.9063759511026203
iteration 15 d= 0.9063759511026203
iteration 16 d= 0.9063759511026203
iteration 17 d= 0.9063759511026203
iteration 18 d= 0.9063759511026203
iteration 19 d= 0.9063759511026203
longueur min 0.9063759511026203

Text(0.0029518595420675586, 0.9531251807206456, 'N-1')