Calculs de surface et autres calculs¶
C’est l’histoire d’une boucle, puis d’une autre, puis enfin d’un couple de boucles, voire d’un triplé.
Enoncé¶
Exercice 1 : calcul de la surface d’un cercle¶
On cherche à écrire une fonction qui calcule la surface d’un cercle de rayon r.
[1]:
def surface_cerle(r):
# ...
return 0.0
1.1 En utilisant la constante pi¶
[ ]:
1.2 Sans utiliser pi ni aucune autre fonction¶
Donc juste des additions, des multiplications, des divisions. On a le droit aux boucles aussi.
[ ]:
Exercice 2 : tri aléatoire¶
On implémente le tri suivant (est-ce vraiment un tri d’ailleurs ?) :
Dans un tableau T, on tire deux élements aléatoires i < j, si T[i] > T[j], on les permute.
On s’arrête après n tirages sans permutations.
Exercice 3 : petits calculs parfaits pour une machine¶
On suppose que le tableau précédent est de taille n=10, l’algorithme précédent s’arrête après n tirages sans permutations. Comment choisir n de telle sorte que le tableau finisse trié dans 90% des cas…
Réponses¶
1.1. calcul de la surface d’un cercle avec pi¶
[2]:
from math import pi
def surface_cercle(r):
return r**2 * pi
surface_cercle(5)
[2]:
78.53981633974483
1.2. calcul de la surface d’un cercle sans pi ou autre fonction¶
Une approche possible est probabiliste : on construit un estimateur de en tirant aléatoirement des points dans un carré de côté 1. Si le point
tombe dans le quart de cercle inscrit dans le carré, on compte 1, sinon on compte 0. Donc:
Ce ratio converge vers la probabilité pour le point de tomber dans le quart de cercle, qui est égale au ratio des deux aires :
avec $ r=1$.
[3]:
import numpy
def estimation_pi(n=10000):
rnd = numpy.random.rand(1000, 2)
norme = rnd[:, 0] ** 2 + rnd[:, 1] ** 2
dedans = norme <= 1
dedans_entier = dedans.astype(numpy.int64)
return dedans_entier.sum() / dedans.shape[0] * 4
pi = estimation_pi()
pi
[3]:
3.216
[4]:
def surface_cercle_pi(r, pi):
return r**2 * pi
surface_cercle_pi(5, pi)
[4]:
80.4
2. tri aléatoire¶
[5]:
def tri_alea(T, n=1000):
T = T.copy()
for i in range(0, n):
i, j = numpy.random.randint(0, len(T), 2)
if i < j and T[i] > T[j]:
T[i], T[j] = T[j], T[i]
return T
tableau = [1, 3, 4, 5, 3, 2, 7, 11, 10, 9, 8, 0]
tri_alea(tableau)
[5]:
[0, 1, 2, 3, 3, 4, 5, 7, 8, 9, 10, 11]
Et si i > j, on ne fait rien et c’est bien dommage.
[6]:
def tri_alea2(T, n=1000):
T = T.copy()
for i in range(0, n):
i = numpy.random.randint(0, len(T) - 1)
j = numpy.random.randint(i + 1, len(T))
if T[i] > T[j]:
T[i], T[j] = T[j], T[i]
return T
tableau = [1, 3, 4, 5, 3, 2, 7, 11, 10, 9, 8, 0]
tri_alea2(tableau)
[6]:
[0, 1, 2, 3, 3, 4, 5, 7, 8, 9, 10, 11]
Le résultat n’est pas forcément meilleur mais il est plus rapide à obtenir puisqu’on fait un test en moins.
Et si on s’arrête quand cinq permutations aléatoires de suite ne mènen à aucune permutations dans le tableau.
[7]:
def tri_alea3(T, c=100):
T = T.copy()
compteur = 0
while compteur < c:
i = numpy.random.randint(0, len(T) - 1)
j = numpy.random.randint(i + 1, len(T))
if T[i] > T[j]:
T[i], T[j] = T[j], T[i]
compteur = 0
else:
compteur += 1
return T
tableau = [1, 3, 4, 5, 3, 2, 7, 11, 10, 9, 8, 0]
tri_alea3(tableau)
[7]:
[0, 1, 2, 3, 3, 4, 5, 7, 8, 9, 10, 11]
3. petits calculs parfaits pour une machine¶
[8]:
def est_trie(T):
for i in range(1, len(T)):
if T[i] < T[i - 1]:
return False
return True
[9]:
def eval_c(n, c, N=100):
compteur = 0
for i in range(N):
T = numpy.random.randint(0, 20, n)
T2 = tri_alea3(T, c=c)
if est_trie(T2):
compteur += 1
return compteur * 1.0 / N
eval_c(10, 100)
[9]:
0.76
[10]:
from tqdm import tqdm # pour afficher une barre de défilement
cs = []
ecs = []
for c in tqdm(range(1, 251, 25)):
cs.append(c)
ecs.append(eval_c(10, c=c))
ecs[-5:]
50%|█████ | 5/10 [00:01<00:01, 3.71it/s]100%|██████████| 10/10 [00:03<00:00, 3.14it/s]
[10]:
[0.88, 0.96, 0.97, 0.95, 0.98]
[11]:
%matplotlib inline
[12]:
import matplotlib.pyplot as plt
plt.plot(cs, ecs)
plt.plot([0, max(cs)], [0.9, 0.9], "--");
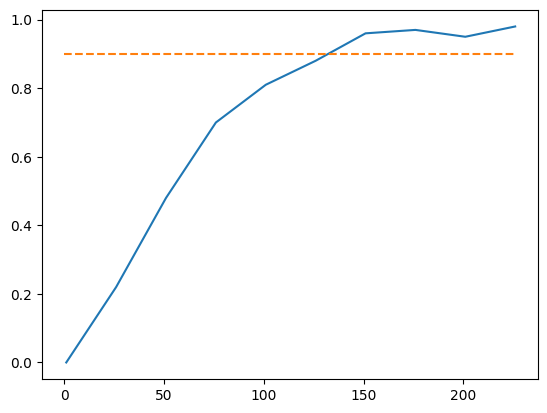
La réponse se situe aux alentours de 150, on ne peut pas dire précisément car tout est aléatoire, on peut seulement estimer la distribution de ce résultat qui est aussi une variable aléatoire. Cette réponse dépend de la taille du tableau à tirer.
[ ]: