Note

Go to the end to download the full example code.

Float Conversion

I came up with the following question (float64)x < (float64)y \Longrightarrow (float32) x < (float32)y? What is the probability this holds?

Probability (float64)x == (float32)x

Let’s evaluate how many time we draw a random double number equal to its float conversion.

import random
import numpy
import pandas
import matplotlib.pyplot as plt

rnd = numpy.random.random(100000000)
rnd.shape, rnd.dtype

((100000000,), dtype('float64'))

rnd32 = rnd.astype(numpy.float32).astype(numpy.float64)
equal = (rnd == rnd32).sum()
equal

np.int64(2)

It is very low. Let’s check the reverse is true.

rnd32b = rnd32.astype(numpy.float64).astype(numpy.float32)
equal = (rnd32b == rnd32).sum()
equal

np.int64(100000000)

Let’s study the distribution of the difference.

delta = rnd - rnd32
numpy.min(delta), numpy.max(delta)

(np.float64(-2.9802321055427683e-08), np.float64(2.9802321721561498e-08))

numpy.min(rnd), numpy.max(rnd)

(np.float64(1.0039616360479897e-08), np.float64(0.9999999966702148))

plt.hist(delta, bins=1000)
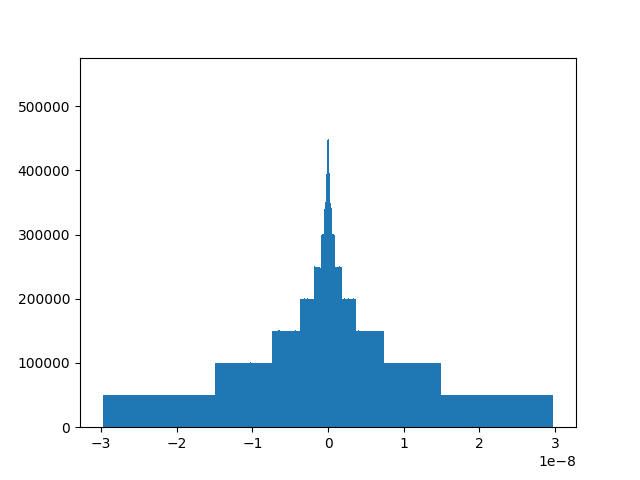
plot float and double rouding
(array([ 49881.,  49760.,  49822.,  49977.,  49720.,  50207.,  49620.,
        50194.,  50275.,  49983.,  50492.,  49723.,  49813.,  50343.,
        50042.,  50261.,  50351.,  49860.,  49856.,  49400.,  50135.,
        49675.,  49996.,  50042.,  50082.,  50008.,  50141.,  49998.,
        50102.,  49972.,  50141.,  49913.,  49822.,  50547.,  50224.,
        49780.,  49479.,  50804.,  50014.,  49697.,  49911.,  49937.,
        50068.,  49981.,  49893.,  49773.,  49813.,  49993.,  49765.,
        50270.,  50178.,  50029.,  50251.,  50330.,  49851.,  49771.,
        49868.,  49508.,  50625.,  50066.,  50462.,  50129.,  50270.,
        49713.,  50290.,  50098.,  50045.,  50071.,  50289.,  49997.,
        49885.,  49712.,  49907.,  50208.,  50105.,  49946.,  50189.,
        50177.,  50124.,  50176.,  50171.,  50164.,  49910.,  50089.,
        50297.,  49783.,  49979.,  49946.,  49933.,  49747.,  49723.,
        50431.,  50063.,  50115.,  49804.,  49914.,  50018.,  49894.,
        49686.,  49618.,  49967.,  49933.,  50389.,  49853.,  49729.,
        49835.,  49959.,  50057.,  49626.,  49878.,  50164.,  50364.,
        50428.,  49926.,  50081.,  49721.,  50388.,  50078.,  50100.,
        49928.,  49620.,  50098.,  49934.,  50281.,  50174.,  49695.,
        49724.,  49912.,  50395.,  49694.,  50626.,  50132.,  50257.,
        49985.,  49749.,  49935.,  49781.,  50120.,  50234.,  49975.,
        50063.,  50436.,  49874.,  50397.,  49972.,  49938.,  49716.,
        50325.,  50375.,  49998.,  49849.,  50214.,  49771.,  49845.,
        49920.,  49965.,  49781.,  49994.,  50071.,  50086.,  50023.,
        49876.,  50397.,  50403.,  50247.,  49810.,  49899.,  49457.,
        50273.,  50052.,  49672.,  50048.,  49929.,  49946.,  49394.,
        50007.,  49837.,  50576.,  50007.,  50326.,  50208.,  50219.,
        49978.,  50156.,  50555.,  49886.,  49692.,  50646.,  49828.,
        50176.,  49909.,  50143.,  49414.,  50031.,  50093.,  50002.,
        49879.,  49672.,  50118.,  50371.,  50023.,  49794.,  49540.,
        50094.,  49724.,  50226.,  50148.,  49854.,  49906.,  49976.,
        49876.,  49908.,  49779.,  49520.,  50220.,  49971.,  49844.,
        49957.,  50260.,  49691.,  50189.,  49745.,  50106.,  50064.,
        50257.,  49967.,  49977.,  50416.,  49784.,  49950.,  49921.,
        49615.,  49984.,  49934.,  49737.,  50154.,  50184.,  49675.,
        49883.,  50353.,  50238.,  50129.,  50071.,  49623.,  50124.,
        49990.,  50300.,  50306.,  50103.,  50254.,  99761., 100250.,
       100031., 100011., 100239., 100127., 100003., 100362., 100646.,
       100302., 100088.,  99848., 100454.,  99638., 100199., 100002.,
       100304.,  99733.,  99658.,  99776.,  99972.,  99683.,  99890.,
       100236., 100268.,  99907.,  99862., 100027.,  99816.,  99792.,
       100044., 100163., 100402.,  99801., 100334.,  99975., 100188.,
       100280.,  99428.,  99635., 100213.,  99966.,  99564., 100156.,
        99923., 100550.,  99704.,  99662.,  99888., 100073.,  99833.,
        99366.,  99678., 100022., 100147., 100205.,  99595., 100112.,
       100065.,  99647.,  99733.,  99782.,  99965., 100173., 100312.,
       100060.,  99988.,  99701.,  99791., 100420.,  99869., 100634.,
        99593.,  99874.,  99437., 100274.,  99766., 100622.,  99981.,
        99998.,  99721., 100507., 100108., 100459.,  99188.,  99960.,
        99963.,  99867.,  99975.,  99971.,  99989.,  99831.,  99769.,
        99999.,  99892., 100035., 100047., 100051.,  99652.,  99584.,
        99795., 100078., 100368., 100352.,  99948.,  99737., 100342.,
       100290.,  99972., 100057.,  99691., 100107., 100268.,  99369.,
       100219., 100056., 100330., 100302.,  99427.,  99916., 100405.,
        99753., 100679., 100094., 100167., 149814., 150582., 150226.,
       149548., 150304., 149794., 149487., 149281., 150180., 149813.,
       150559., 150285., 150457., 149774., 150031., 150003., 149935.,
       150172., 149961., 150075., 150821., 150263., 150854., 149899.,
       149261., 149447., 150478., 150181., 150416., 149354., 149825.,
       149462., 150501., 150313., 150806., 150450., 149795., 150568.,
       149880., 149587., 150048., 150080., 149961., 149478., 150148.,
       150241., 150315., 149939., 149831., 149488., 151002., 150070.,
       150272., 150015., 149839., 150375., 149370., 149545., 150110.,
       149868., 150044., 150366., 174793., 199305., 200405., 199913.,
       199877., 200523., 200346., 199816., 200467., 200421., 200567.,
       199550., 200227., 200162., 200584., 200104., 199527., 200743.,
       200065., 200639., 199817., 199467., 199913., 199716., 199964.,
       199361., 199902., 199744., 200708., 199494., 199734., 213020.,
       250105., 249709., 250532., 249578., 249913., 249605., 249830.,
       250662., 250068., 249995., 249608., 251195., 249997., 249481.,
       250484., 281486., 299973., 300075., 299546., 299904., 299631.,
       300202., 300244., 340428., 350159., 350561., 350232., 394982.,
       399543., 447526., 547856., 547156., 447780., 399553., 395526.,
       349630., 350521., 350203., 340488., 300922., 300119., 298875.,
       300390., 299630., 300077., 299250., 281726., 250291., 249367.,
       249677., 250192., 250151., 250093., 250473., 250299., 249152.,
       250599., 249853., 249723., 250827., 249446., 249731., 211926.,
       200513., 200555., 199666., 200123., 199909., 200050., 199825.,
       200051., 200010., 199752., 199540., 200495., 199487., 200393.,
       200254., 200152., 200402., 200411., 200406., 199892., 199574.,
       199615., 199844., 199911., 200133., 199704., 200044., 200552.,
       199685., 199970., 174703., 150413., 150744., 150243., 150343.,
       149915., 149910., 149832., 150260., 149691., 149770., 150078.,
       149808., 149844., 150269., 149744., 150494., 149891., 150088.,
       150059., 150614., 149710., 150152., 150013., 150279., 150136.,
       150383., 150350., 150282., 149837., 149864., 150102., 150043.,
       150050., 149974., 150556., 150067., 149104., 149330., 150040.,
       149675., 149745., 149618., 149877., 150015., 149658., 149976.,
       149717., 150142., 149621., 149562., 149731., 150016., 150543.,
       150132., 149645., 149487., 149488., 150304., 149225., 149046.,
       150489., 150083.,  99741.,  99691., 100032., 100138.,  99720.,
        99799., 100116., 100174., 100197., 100195.,  99772., 100448.,
       100434.,  99595., 100097., 100036.,  99905.,  99716., 100016.,
       100159.,  99473., 100038.,  99923.,  99592.,  99618.,  99987.,
       100172.,  99638., 100023., 100361., 100520., 100171.,  99864.,
        99802.,  99622.,  99548., 100008., 100179.,  99776.,  99786.,
       100085., 100426.,  99545.,  99875., 100116.,  99704., 100032.,
        99503., 100261.,  99761., 100006.,  99878.,  99787., 100178.,
        99846., 100326., 100058.,  99659., 100441., 100182.,  99752.,
        99898., 100069., 100018.,  99729.,  99659.,  99954.,  99724.,
       100411.,  99873., 100077.,  99921.,  99576., 100065.,  99433.,
        99883., 100327.,  99638., 100289.,  99759.,  99968.,  99648.,
       100143.,  99560.,  99982.,  99331., 100054.,  99921.,  99559.,
       100220.,  99998.,  99790., 100459.,  99989.,  99940.,  99852.,
       100115., 100135.,  99580.,  99612.,  99603.,  99910.,  99957.,
       100346., 100512., 100012., 100292.,  99655., 100167., 100889.,
        99831.,  99816.,  99965., 100000., 100371.,  99896., 100208.,
       100083., 100353., 100058., 100255.,  99838.,  99583., 100289.,
        99616.,  50373.,  50012.,  49859.,  50224.,  49652.,  49378.,
        49851.,  49884.,  49648.,  50034.,  49705.,  49848.,  50262.,
        50072.,  49731.,  49914.,  49792.,  49998.,  49766.,  49993.,
        49942.,  49796.,  49836.,  49936.,  50114.,  50030.,  50096.,
        49299.,  50098.,  50315.,  50262.,  49476.,  50315.,  49949.,
        50123.,  50095.,  50301.,  50208.,  50086.,  49598.,  50132.,
        50119.,  49859.,  49930.,  50273.,  49998.,  50167.,  50123.,
        50132.,  49776.,  50091.,  49885.,  49819.,  50164.,  50217.,
        49974.,  49797.,  50056.,  50267.,  50245.,  49763.,  50322.,
        49835.,  50084.,  50410.,  50044.,  50353.,  50310.,  50072.,
        50295.,  49856.,  49943.,  49865.,  49855.,  50224.,  50190.,
        49776.,  50076.,  50164.,  49944.,  49560.,  49740.,  49522.,
        50092.,  50228.,  50070.,  49875.,  50030.,  49995.,  49967.,
        49759.,  49776.,  49993.,  49737.,  49816.,  50334.,  49955.,
        49774.,  50123.,  50137.,  49848.,  50164.,  49934.,  49701.,
        49708.,  49899.,  49676.,  50185.,  49953.,  49879.,  49689.,
        50204.,  50318.,  50044.,  50279.,  49834.,  50145.,  49821.,
        50119.,  50348.,  49986.,  49986.,  49869.,  50429.,  49762.,
        50245.,  50360.,  50393.,  50083.,  50139.,  50253.,  50194.,
        49773.,  49953.,  49804.,  49983.,  50077.,  49690.,  49986.,
        49958.,  49915.,  50195.,  50467.,  50168.,  49956.,  50217.,
        49940.,  50102.,  49772.,  50496.,  50199.,  50014.,  49914.,
        49884.,  49983.,  50065.,  49769.,  49658.,  49880.,  50234.,
        49694.,  49635.,  49332.,  50192.,  49844.,  50133.,  49774.,
        50203.,  49928.,  50223.,  49826.,  50149.,  49807.,  50122.,
        50110.,  49853.,  50166.,  50252.,  49708.,  49664.,  50273.,
        49819.,  50095.,  49803.,  50161.,  50136.,  49718.,  49973.,
        50265.,  49612.,  50251.,  50127.,  50165.,  49855.,  50043.,
        50009.,  50634.,  49955.,  49799.,  50034.,  49816.,  49961.,
        49699.,  50052.,  50459.,  50257.,  50304.,  49856.,  49836.,
        50001.,  49778.,  50155.,  50013.,  50147.,  49794.,  49710.,
        50165.,  49839.,  50144.,  50618.,  49974.,  50188.,  50070.,
        50226.,  49738.,  49736.,  50097.,  50336.,  49710.,  50059.,
        49767.,  50050.,  49700.,  50366.,  49925.,  50067.,  49849.,
        50143.,  49665.,  49677.,  50151.,  50231.,  50059.,  50209.,
        50214.,  50066.,  49717.,  49750.,  49731.,  50291.]), array([-2.98023211e-08, -2.97427164e-08, -2.96831118e-08, ...,
        2.96831124e-08,  2.97427171e-08,  2.98023217e-08], shape=(1001,)), <BarContainer object of 1000 artists>)

We finally check that double operations between float numpers remain floats.

for i in range(100000):
    i, j = random.randint(0, len(rnd32) - 1), random.randint(0, len(rnd32) - 1)
    d32 = numpy.float64(rnd32[i] * rnd32[j])
    d64 = numpy.float64(rnd32[i]) * numpy.float64(rnd32[j])
    if d32 != d64:
        raise AssertionError(
            "Issue with somme={0} = {1} + {2}".format(
                rnd32[i] + rnd32[j], rnd32[i], rnd32[j]
            )
        )

Interval length distribution

Let’s imagine now we want to define an intervalle in which a double is converted to the same float. Let’s find out about it length.

def find_interval(x):
    dx = numpy.abs(x - numpy.float32(x))  # usually not zero
    dx /= 100
    f = numpy.float32(x)
    x1 = x
    while numpy.float32(x1) == f:
        x1 -= dx
    x2 = x
    while numpy.float32(x2) == f:
        x2 += dx
    return x1 + dx, x2 - dx


length = numpy.zeros((2000,))
for i in range(length.shape[0]):
    x = rnd[i]
    x1, x2 = find_interval(x)
    length[i] = x2 - x1

min(length), max(length)

(np.float64(7.2437805265831295e-12), np.float64(5.960462257093013e-08))

plt.hist(length, bins=50)
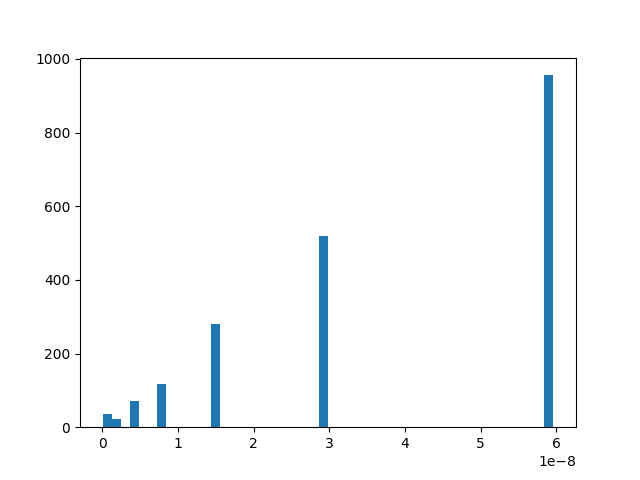
plot float and double rouding
(array([  27.,   28.,    0.,   60.,    0.,    0.,  120.,    0.,    0.,
          0.,    0.,    0.,  250.,    0.,    0.,    0.,    0.,    0.,
          0.,    0.,    0.,    0.,    0.,    0.,  480.,    0.,    0.,
          0.,    0.,    0.,    0.,    0.,    0.,    0.,    0.,    0.,
          0.,    0.,    0.,    0.,    0.,    0.,    0.,    0.,    0.,
          0.,    0.,    0.,    0., 1035.]), array([7.24378053e-12, 1.19919136e-09, 2.39113893e-09, 3.58308651e-09,
       4.77503408e-09, 5.96698166e-09, 7.15892924e-09, 8.35087681e-09,
       9.54282439e-09, 1.07347720e-08, 1.19267195e-08, 1.31186671e-08,
       1.43106147e-08, 1.55025623e-08, 1.66945098e-08, 1.78864574e-08,
       1.90784050e-08, 2.02703526e-08, 2.14623001e-08, 2.26542477e-08,
       2.38461953e-08, 2.50381429e-08, 2.62300904e-08, 2.74220380e-08,
       2.86139856e-08, 2.98059332e-08, 3.09978808e-08, 3.21898283e-08,
       3.33817759e-08, 3.45737235e-08, 3.57656711e-08, 3.69576186e-08,
       3.81495662e-08, 3.93415138e-08, 4.05334614e-08, 4.17254089e-08,
       4.29173565e-08, 4.41093041e-08, 4.53012517e-08, 4.64931992e-08,
       4.76851468e-08, 4.88770944e-08, 5.00690420e-08, 5.12609895e-08,
       5.24529371e-08, 5.36448847e-08, 5.48368323e-08, 5.60287798e-08,
       5.72207274e-08, 5.84126750e-08, 5.96046226e-08]), <BarContainer object of 50 artists>)

So we can approximate this interval by something like this:

ql = numpy.sort(length)[int(length.shape[0] * 0.8)]
ql

np.float64(5.9532995866362626e-08)

An answer to the initial question

Let’s estimate \mathbb{P}\left(x_{64} < y_{64} \Longrightarrow x_{32} < y_{32} \; | \; |x-y| \leqslant d\right) ?

def inf_strict(x, y):
    f1 = x < y
    f2 = numpy.float32(x) < numpy.float32(y)
    return f1, f2


def count_events(fct):
    rows = []
    for di in range(1, 1001):
        d = di * ql / 100
        total = 0
        ok = 0
        rnd = numpy.random.random((2000 * 3,))
        for i in range(0, rnd.shape[0], 3):
            s = -1 if rnd[i + 2] < 0.5 else 1
            x, y = rnd[i], rnd[i] + rnd[i + 1] * d * s
            f1, f2 = fct(x, y)
            if f1:
                total += 1
                if f2:
                    ok += 1
        if (di + 10) % 100 == 0:
            print(di, d, ":", ok, total)
        rows.append(dict(d=d, ratio=ok * 1.0 / total, total=total))

    return pandas.DataFrame(rows)


df = count_events(inf_strict)
df.head()

90 5.357969627972636e-08 : 618 983
190 1.1311269214608899e-07 : 848 1027
290 1.7264568801245163e-07 : 892 1000
390 2.3217868387881425e-07 : 980 1071
490 2.917116797451769e-07 : 981 1046
590 3.512446756115395e-07 : 923 981
690 4.1077767147790213e-07 : 923 968
790 4.7031066734426475e-07 : 922 958
890 5.298436632106273e-07 : 968 997
990 5.8937665907699e-07 : 987 1021
d ratio total
0 5.953300e-10 0.023139 994
1 1.190660e-09 0.049049 999
2 1.785990e-09 0.055992 1018
3 2.381320e-09 0.082653 980
4 2.976650e-09 0.110212 989 


df.plot(x="d", y="ratio")
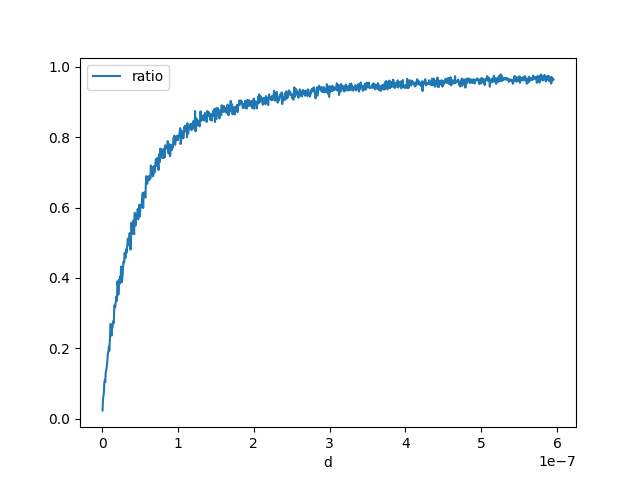
plot float and double rouding
<Axes: xlabel='d'>

df.plot(x="d", y="ratio", logx=True)
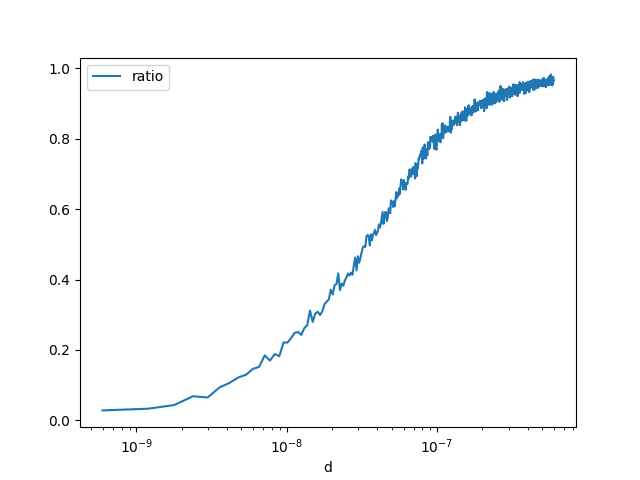
plot float and double rouding
<Axes: xlabel='d'>

An answer to a similar question: what about not strict comparison?

Let’s estimate \mathbb{P}\left(x_{64} \leqslant y_{64} \Longrightarrow x_{32} \leqslant y_{32} \; | \; |x-y| \leqslant d\right) ?

def inf_equal(x, y):
    f1 = x <= y
    f2 = numpy.float32(x) <= numpy.float32(y)
    return f1, f2


df2 = count_events(inf_equal)
df2.head()

90 5.357969627972636e-08 : 983 983
190 1.1311269214608899e-07 : 981 981
290 1.7264568801245163e-07 : 972 972
390 2.3217868387881425e-07 : 1029 1029
490 2.917116797451769e-07 : 1008 1008
590 3.512446756115395e-07 : 1007 1007
690 4.1077767147790213e-07 : 991 991
790 4.7031066734426475e-07 : 996 996
890 5.298436632106273e-07 : 1027 1027
990 5.8937665907699e-07 : 1022 1022
d ratio total
0 5.953300e-10 1.0 1006
1 1.190660e-09 1.0 987
2 1.785990e-09 1.0 977
3 2.381320e-09 1.0 1011
4 2.976650e-09 1.0 998 


ax = df.plot(x="d", y="ratio", logx=True, label="<")
df2.plot(x="d", y="ratio", logx=True, label="<=", ax=ax)
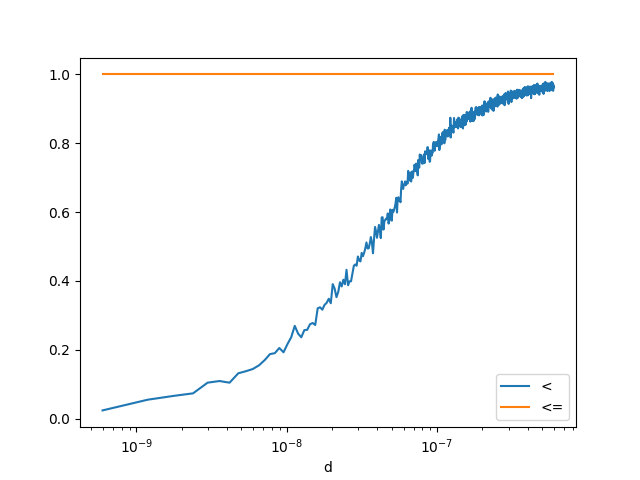
plot float and double rouding
<Axes: xlabel='d'>

def sup_strict(x, y):
    f1 = x > y
    f2 = numpy.float32(x) > numpy.float32(y)
    return f1, f2


df3 = count_events(sup_strict)
df3.head()

90 5.357969627972636e-08 : 629 990
190 1.1311269214608899e-07 : 837 1026
290 1.7264568801245163e-07 : 881 1019
390 2.3217868387881425e-07 : 893 996
490 2.917116797451769e-07 : 967 1032
590 3.512446756115395e-07 : 940 1013
690 4.1077767147790213e-07 : 941 999
790 4.7031066734426475e-07 : 957 999
890 5.298436632106273e-07 : 950 1000
990 5.8937665907699e-07 : 949 979
d ratio total
0 5.953300e-10 0.022000 1000
1 1.190660e-09 0.049950 1001
2 1.785990e-09 0.057436 975
3 2.381320e-09 0.059339 1028
4 2.976650e-09 0.093280 997 


ax = df.plot(x="d", y="ratio", logx=True, label="<")
df2.plot(x="d", y="ratio", logx=True, label="<=", ax=ax)
df3.plot(x="d", y="ratio", logx=True, label=">", ax=ax)
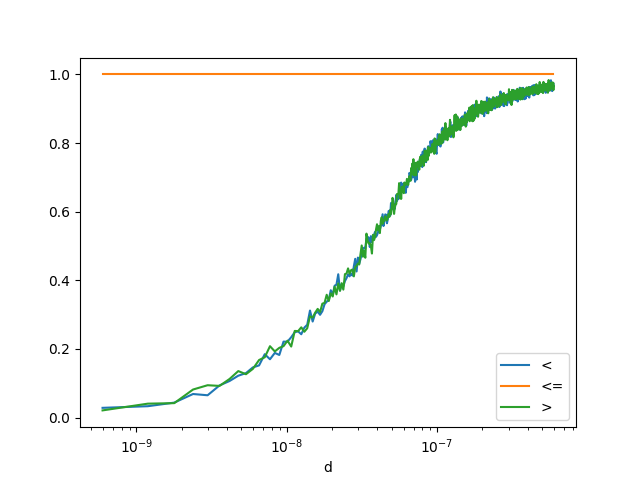
plot float and double rouding
<Axes: xlabel='d'>

def sup_equal(x, y):
    f1 = x >= y
    f2 = numpy.float32(x) >= numpy.float32(y)
    return f1, f2


df4 = count_events(sup_equal)
df4.head()

90 5.357969627972636e-08 : 1033 1033
190 1.1311269214608899e-07 : 1012 1012
290 1.7264568801245163e-07 : 999 999
390 2.3217868387881425e-07 : 1022 1022
490 2.917116797451769e-07 : 1003 1003
590 3.512446756115395e-07 : 1018 1018
690 4.1077767147790213e-07 : 995 995
790 4.7031066734426475e-07 : 978 978
890 5.298436632106273e-07 : 973 973
990 5.8937665907699e-07 : 1002 1002
d ratio total
0 5.953300e-10 1.0 1002
1 1.190660e-09 1.0 1007
2 1.785990e-09 1.0 999
3 2.381320e-09 1.0 1038
4 2.976650e-09 1.0 967 


ax = df.plot(x="d", y="ratio", logx=True, label="<")
df2.plot(x="d", y="ratio", logx=True, label="<=", ax=ax)
df3.plot(x="d", y="ratio", logx=True, label=">", ax=ax)
df4.plot(x="d", y="ratio", logx=True, label=">=", ax=ax)
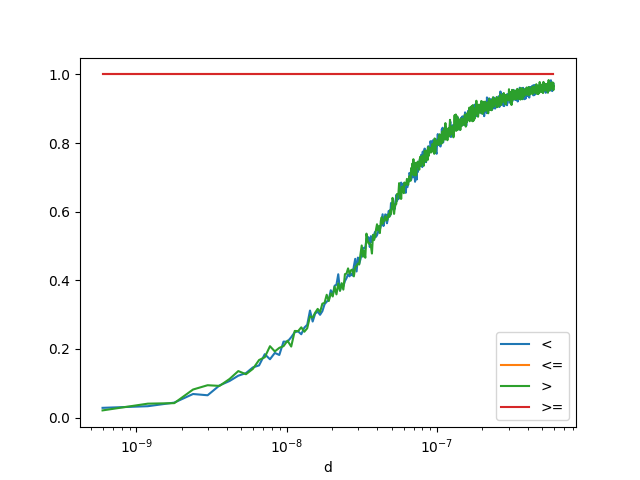
plot float and double rouding
<Axes: xlabel='d'>

def inf_strict_neg(x, y):
    f1 = (-x) >= (-y)
    f2 = (-numpy.float32(x)) >= (-numpy.float32(y))
    return f1, f2


dfn = count_events(inf_strict_neg)
dfn.head()

90 5.357969627972636e-08 : 1053 1053
190 1.1311269214608899e-07 : 961 961
290 1.7264568801245163e-07 : 1006 1006
390 2.3217868387881425e-07 : 1024 1024
490 2.917116797451769e-07 : 987 987
590 3.512446756115395e-07 : 1008 1008
690 4.1077767147790213e-07 : 995 995
790 4.7031066734426475e-07 : 967 967
890 5.298436632106273e-07 : 1002 1002
990 5.8937665907699e-07 : 1025 1025
d ratio total
0 5.953300e-10 1.0 1018
1 1.190660e-09 1.0 997
2 1.785990e-09 1.0 1040
3 2.381320e-09 1.0 988
4 2.976650e-09 1.0 998 


ax = df.plot(x="d", y="ratio", logx=True, label="<")
dfn.plot(x="d", y="ratio", logx=True, label="-1 x >=", ax=ax)
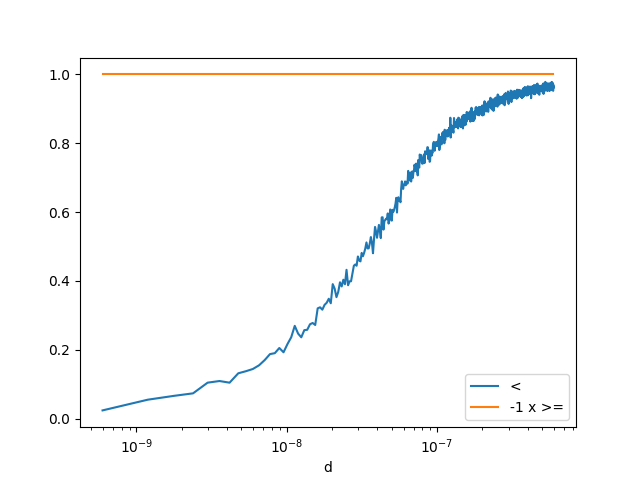
plot float and double rouding
<Axes: xlabel='d'>

Conclusion

The result is expected. As soon as two float are rounded to the same value, the strict inequality no longer holds. However, if you need to write a code which has to handle double and float (in a template for example), you should use not strict inequalities. It is easier to compare the results but you should read some article like Is < faster than <=?. According to Processing costs of non-strict versus strict comparison, < is 5-10% faster than <=.

Total running time of the script: (0 minutes 19.161 seconds)

Gallery generated by Sphinx-Gallery