1A - Enoncé 3 mars 2022- rattrapage¶
Correction de l’examen du 3 mars 2022. L’objectif est de construire un arbre de façon algorithmique.
Dessin d’une liste de segments¶
[2]:
import matplotlib.pyplot as plt
def draw(segments, L=1):
fig, ax = plt.subplots(1, 1, figsize=(4, 4))
maxxy = 0
for seg in segments:
ax.plot(
[seg["x1"], seg["x2"]], [seg["y1"], seg["y2"]], "b-", lw=seg["E"] * 10000
)
ax.set_xlim([0, 2 * L])
ax.set_ylim([-L, L])
return ax
draw([{"x1": 0, "y1": 0, "x2": 1.0, "y2": 0.0, "E": 0.001, "angle": 0}]);

Distance d’un segment¶
[3]:
def distance(seg):
x1, x2, y1, y2 = seg["x1"], seg["x2"], seg["y1"], seg["y2"]
return ((x2 - x1) ** 2 + (y2 - y1) ** 2) ** 0.5
distance({"x1": 0, "y1": 0, "x2": 1.0, "y2": 0.0, "E": 0.001, "angle": 0})
[3]:
1.0
Calcul du segment suivant¶
[4]:
from math import cos, sin, pi
def segment(x=0, y=0, angle=0, L=1, E=0.001):
x2 = x + cos(angle) * L
y2 = y + sin(angle) * L
return dict(x1=x, y1=y, x2=x2, y2=y2, E=E, angle=angle)
segment()
[4]:
{'x1': 0, 'y1': 0, 'x2': 1.0, 'y2': 0.0, 'E': 0.001, 'angle': 0}
Calcul des trois segments suivants¶
[5]:
def tree3(seg, angle=pi / 3, re=0.33, rl=0.66):
x, y = seg["x2"], seg["y2"]
e = seg["E"] * re
le = distance(seg) * rl
a = seg["angle"]
segments = [
segment(x, y, angle=a - angle, L=le, E=e),
segment(x, y, angle=a, L=le, E=e),
segment(x, y, angle=a + angle, L=le, E=e),
]
return segments
premier = segment()
segs = [premier] + tree3(premier, 1)
draw(segs);
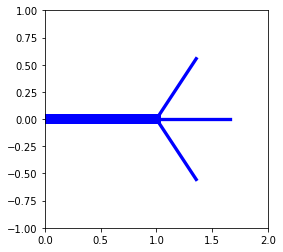
Construction de tous les niveaux de l’arbre¶
[6]:
def tree_recursive(level, seg, angle=pi / 6, re=0.6, rl=0.95):
all_segs = [seg]
iter_segs = [seg]
for i in range(level):
new_segs = []
for seg in iter_segs:
new_segs.extend(tree3(seg, angle=angle, re=re, rl=rl))
all_segs.extend(new_segs)
iter_segs = new_segs
return all_segs
premier = segment()
segs = tree_recursive(3, premier)
draw(segs, L=3);

Construction de trois segments aléatoires¶
[7]:
import random
def tree3_alea(seg, angle=pi / 3, re=0.33, rl=0.66, rnd=0.1):
re_rnd = re * (1 + random.random() * rnd)
rl_rnd = rl * (1 + random.random() * rnd)
x, y = seg["x2"], seg["y2"]
e = seg["E"] * re_rnd
le = distance(seg) * rl_rnd
a = seg["angle"]
a1 = a - (1 + random.random() * rnd) * angle
a2 = a + random.random() * rnd * angle
a3 = a + (1 + random.random() * rnd) * angle
segments = [
segment(x, y, angle=a1, L=le, E=e),
segment(x, y, angle=a2, L=le, E=e),
segment(x, y, angle=a3, L=le, E=e),
]
return segments
premier = segment()
segs = [premier] + tree3_alea(premier, 1)
draw(segs);
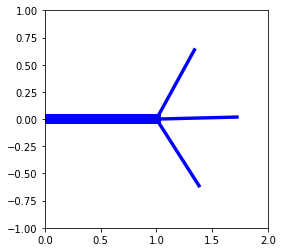
Construction d’un arbre aléatoire¶
L’idée est d’ajouter 40% d’aléatoire sur trois paramètres : la réduction des longueurs, la réduction des épaisseurs, les angles des trois segments suivants.
[8]:
def tree_recursive_alea(level, seg, angle=pi / 6, re=0.6, rl=0.95, rnd=0.4):
all_segs = [seg]
iter_segs = [seg]
for i in range(level):
new_segs = []
for seg in iter_segs:
new_segs.extend(tree3_alea(seg, angle=angle, re=re, rl=rl, rnd=rnd))
all_segs.extend(new_segs)
iter_segs = new_segs
return all_segs
premier = segment()
segs = tree_recursive_alea(3, premier)
draw(segs, L=3.5);
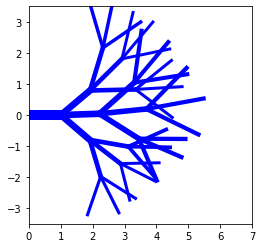
[9]:
premier = segment()
segs = tree_recursive_alea(4, premier)
draw(segs, L=5);

[10]: