Recherche dichotomique#

Recherche dichotomique illustrée.

Lorsqu’on décrit n’importe quel algorithme, on évoque toujours son coût, souvent une formule de ce style :

$O(n^u(\ln_2 n)^v)$

$u$ et $v$ sont des entiers. $v$ est souvent soit 0, soit 1. Mais d’où vient ce logarithme ? Le premier algorithme auquel on pense et dont le coût correspond au cas $u=0$ et $v=1$ est la recherche dichotomique. Il consiste à chercher un élément dans une liste triée. Le logarithme vient du fait qu’on réduit l’espace de recherche par deux à chaque itération. Fatalement, on trouve très vite l’élément à chercher. Et le logarithme, dans la plupart des algorithmes, vient du fait qu’on divise la dimension du problème par un nombre entier à chaque itération, ici 2.

La recherche dichotomique est assez simple : on part d’une liste triée T et on cherche l’élément v (on suppose qu’il s’y trouve). On procède comme suit :

On compare v à l’élément du milieu de la liste.
S’il est égal à v, on a fini.
Sinon, s’il est inférieur, il faut chercher dans la première moitié de la liste. On retourne à l’étape 1 avec la liste réduite.
S’il est supérieur, on fait de même avec la seconde moitié de la liste.

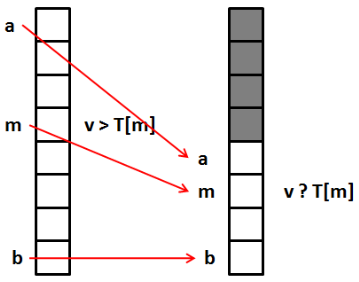
C’est ce qu’illustre la figure suivante où a désigne le début de la liste, b la fin, m le milieu. A chaque itération, on déplace ces trois positions.

[2]:

from IPython.display import Image

Image("images/dicho.png")

[2]:

../../_images/practice_py-base_recherche_dichotomique_2_0.png

Version itérative#

[3]:

def recherche_dichotomique(element, liste_triee):
    a = 0
    b = len(liste_triee) - 1
    m = (a + b) // 2
    while a < b:
        if liste_triee[m] == element:
            return m
        elif liste_triee[m] > element:
            b = m - 1
        else:
            a = m + 1
        m = (a + b) // 2
    return a

[4]:

li = [0, 4, 5, 19, 100, 200, 450, 999]
recherche_dichotomique(5, li)

[4]:

Version récursive#

[5]:

def recherche_dichotomique_recursive(element, liste_triee, a=0, b=-1):
    if a == b:
        return a
    if b == -1:
        b = len(liste_triee) - 1
    m = (a + b) // 2
    if liste_triee[m] == element:
        return m
    elif liste_triee[m] > element:
        return recherche_dichotomique_recursive(element, liste_triee, a, m - 1)
    else:
        return recherche_dichotomique_recursive(element, liste_triee, m + 1, b)

[6]:

recherche_dichotomique(5, li)

[6]:

Version récursive 2#

L’ajout des parametrès a et b peut paraître un peu lourd. Voici une troisième implémentation en Python (toujours récursive) :

[7]:

def recherche_dichotomique_recursive2(element, liste_triee):
    if len(liste_triee) == 1:
        return 0
    m = len(liste_triee) // 2
    if liste_triee[m] == element:
        return m
    elif liste_triee[m] > element:
        return recherche_dichotomique_recursive2(element, liste_triee[:m])
    else:
        return m + recherche_dichotomique_recursive2(element, liste_triee[m:])

[8]:

recherche_dichotomique(5, li)

[8]:

Il ne faut pas oublier m + sinon le résultat peut être décalé dans certains cas. Ensuite, cette version sera un peu moins rapide du fait de la recopie d’une partie de la liste.

[ ]:

Notebook on github