Evaluation Python / Machine Learning année 2017 - solution¶

Le répertoire _data/2017 contient deux fichiers csv simulés aléatoirement dont il faudra se servir pour répondre aux 10 questions qui suivent. Chaque question vaut deux points. Le travail est à rendre pour le lundi 20 février sous la forme d’un notebook envoyé en pièce jointe d’un mail.

[1]:

%matplotlib inline

1¶

Deux fichiers sont extraits de la base de données d’un médecin. Un fichier contient des informations sur des personnes, un autre sur les rendez-vous pris par ces personnes. Quels sont-ils ?

[3]:

import pandas

persons = pandas.read_csv(
    "https://raw.githubusercontent.com/sdpython/teachpyx/main/_data/2017/persons.txt",
    sep="\t",
)
persons.head()

[3]:

	age	gender	idc	name
0	37	0	4ba0b473-f8ca-4466-a65b-40e9b8ba5029	Cendrillon
1	41	0	f44b004b-b01e-4835-b86d-1a42846c6d93	Cendrillon
2	46	1	304895f0-f686-4b0e-8854-a705bb5a6982	Balthazar
3	42	1	3f0d31d2-0ef4-4e7e-b876-07d10225cc8c	Balthazar
4	41	1	f29273f4-a76c-4158-b5f5-b3e5a080a0c7	Balthazar

[4]:

rend = pandas.read_csv(
    "https://raw.githubusercontent.com/sdpython/teachpyx/main/_data/2017/rendezvous.txt",
    sep="\t",
)
rend.head()

[4]:

	date	idc	idr	price
0	2016-12-02 19:47:45.068274	4ba0b473-f8ca-4466-a65b-40e9b8ba5029	b7db0ac9-86a1-46f9-98ac-f1f8eb54072d	75.0
1	2016-12-02 19:47:45.068274	4ba0b473-f8ca-4466-a65b-40e9b8ba5029	a65f721a-de11-4a01-be71-b26e2da3ac00	65.0
2	2016-12-07 19:47:45.068274	f44b004b-b01e-4835-b86d-1a42846c6d93	644b1236-b9ee-4ef5-8ca7-d1adadb547c8	75.0
3	2016-12-17 19:47:45.068274	f44b004b-b01e-4835-b86d-1a42846c6d93	aff6ac9e-5dd0-434e-9888-f724f6d40969	80.0
4	2017-01-07 19:47:45.068274	f44b004b-b01e-4835-b86d-1a42846c6d93	9ca87507-aa95-49a9-88b3-86ec9fbc44d6	80.0

[5]:

persons.shape, rend.shape

[5]:

((1000, 4), (2537, 4))

Le second fichier est plus volumineux et contient une variable price qui ne peut pas être reliée aux personnes. Le premier fichier est celui des personnes, le second celui des rendez-vous. La variable idc est présente dans les deux tables. C’est elle qui identifie les personnes dans les deux tables.

2¶

On souhaite étudier la relation entre le prix moyen payé par une personne, son âge et son genre. Calculer le prix moyen payé par une personne ?

La table des rendez-vous contient toutes l’information nécessaire. La question était un peu ambiguë. On peut déterminer le prix moyen payé par personne, ou le prix moyen des prix moyens… On va répondre à la première option car la seconde n’a pas beaucoup d’intérêt et c’est très proche du prix moyen par rendez-vous, ce que la question aurait sans doute formulé dans ce sens si telle avait été son intention. On groupe par idc et on fait la moyenne.

[8]:

gr = rend[["idc", "price"]].groupby("idc").mean()
gr.head()

[8]:

	price
idc
003b0195-2acb-4f46-b7fa-28cf266a8f60	80.0
009e689c-51a1-4cef-99ca-a4ba364eba8d	80.0
00a213c2-1174-4359-8a67-fe710ec1b439	70.0
00e42818-aade-4758-a5f6-c78a6f235ea5	70.0
0153b785-9acd-4d28-aad1-62f8bf2faea3	75.0

3¶

Faire la jointure entre les deux tables.

[9]:

join = persons.merge(gr.reset_index(), on="idc")
join.head()

[9]:

	age	gender	idc	name	price
0	37	0	4ba0b473-f8ca-4466-a65b-40e9b8ba5029	Cendrillon	70.000000
1	41	0	f44b004b-b01e-4835-b86d-1a42846c6d93	Cendrillon	78.333333
2	46	1	304895f0-f686-4b0e-8854-a705bb5a6982	Balthazar	75.000000
3	42	1	3f0d31d2-0ef4-4e7e-b876-07d10225cc8c	Balthazar	95.000000
4	41	1	f29273f4-a76c-4158-b5f5-b3e5a080a0c7	Balthazar	90.000000

Cette jointure est assez simple puisque la colonne partagée porte le même nom dans les deux tables. On peut néanmoins se poser la question de savoir s’il y a des personnes qui n’ont pas de rendez-vous associé et réciproquement.

[10]:

join.shape

[10]:

(1000, 5)

[11]:

join = persons.merge(gr.reset_index(), on="idc", how="outer")
join.shape

[11]:

(1000, 5)

Visiblement, ce n’est pas le cas puisqu’une jointure incluant les éléments sans correspondances dans les deux tables n’ajoute pas plus d’éléments à la jointure.

4¶

Tracer deux nuages de points (age, prix moyen) et (genre, prix moyen) ?

[13]:

join.plot(x="age", y="price", kind="scatter", title="age / price")

[13]:

<Axes: title={'center': 'age / price'}, xlabel='age', ylabel='price'>

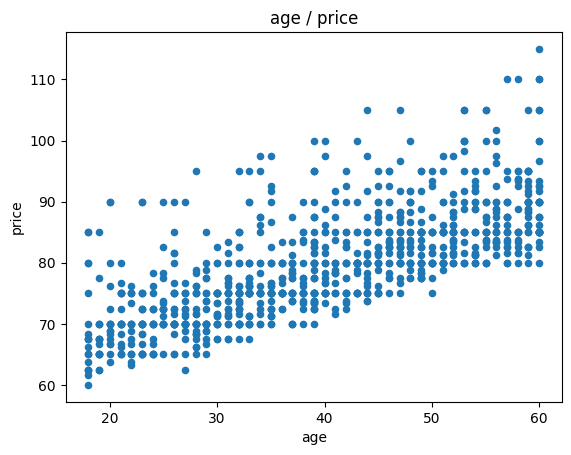
../../_images/practice_exams_enonce_ml_2017_correction_16_1.png

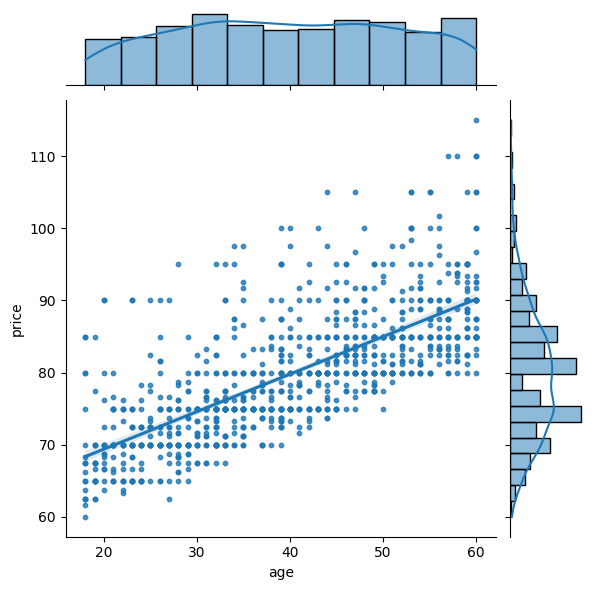
On peut aussi utiliser un module comme seaborn qui propose des dessins intéressants pour un statisticatien.

[16]:

import seaborn

g = seaborn.jointplot(join, x="age", y="price", kind="reg", scatter_kws={"s": 10})

/home/xadupre/.local/lib/python3.10/site-packages/seaborn/_oldcore.py:1119: FutureWarning: use_inf_as_na option is deprecated and will be removed in a future version. Convert inf values to NaN before operating instead.
  with pd.option_context('mode.use_inf_as_na', True):
/home/xadupre/.local/lib/python3.10/site-packages/seaborn/_oldcore.py:1119: FutureWarning: use_inf_as_na option is deprecated and will be removed in a future version. Convert inf values to NaN before operating instead.
  with pd.option_context('mode.use_inf_as_na', True):

../../_images/practice_exams_enonce_ml_2017_correction_18_1.png

[17]:

join.plot(x="gender", y="price", kind="scatter")

[17]:

<Axes: xlabel='gender', ylabel='price'>

../../_images/practice_exams_enonce_ml_2017_correction_19_1.png

On ne voit pas grand chose sur ce second graphe. Une option est d’ajouter un bruit aléatoire sur le genre pour éclater le nuage.

[18]:

import numpy

bruit = join.copy()
bruit["gx"] = bruit.gender + numpy.random.random(bruit.shape[0]) / 3
bruit.plot(x="gx", y="price", kind="scatter")

[18]:

<Axes: xlabel='gx', ylabel='price'>

../../_images/practice_exams_enonce_ml_2017_correction_21_1.png

Il n’y a rien de flagrant. On peut faire un graphe moustache.

[19]:

join[["price", "gender"]].boxplot(by="gender")

[19]:

<Axes: title={'center': 'price'}, xlabel='[gender]'>

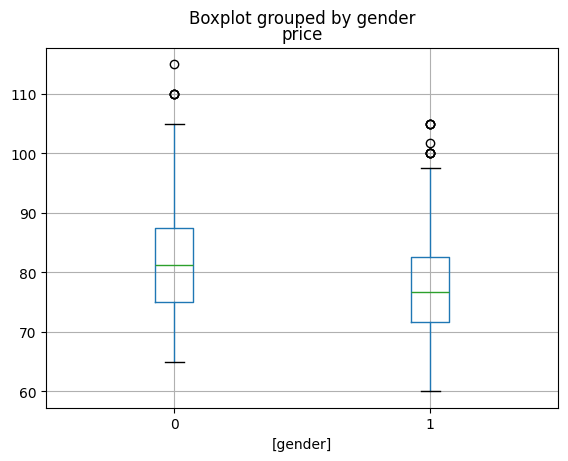
../../_images/practice_exams_enonce_ml_2017_correction_23_1.png

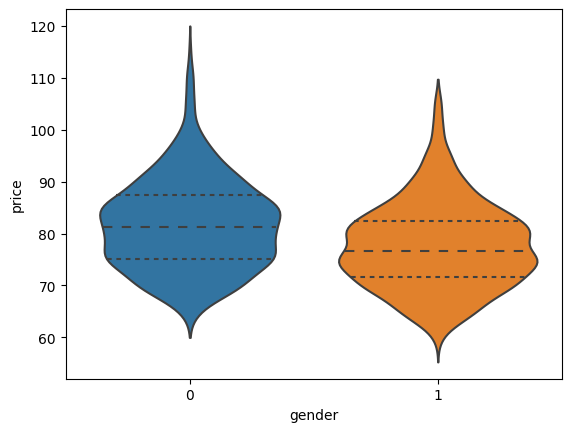
C’est mieux. Un dernier. Le diagramme violon, plus complet que le précédent.

[20]:

seaborn.violinplot(x="gender", y="price", data=join, inner="quart")

[20]:

<Axes: xlabel='gender', ylabel='price'>

../../_images/practice_exams_enonce_ml_2017_correction_25_1.png

5¶

Calculer les coefficients de la régression $prix\_moyen \sim age + genre$ .

Une régression. Le premier réflexe est scikit-learn.

[22]:

from sklearn.linear_model import LinearRegression

lr = LinearRegression()
lr.fit(join[["age", "gender"]], join["price"])

[22]:

LinearRegression()

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

[23]:

lr.coef_

[23]:

array([ 0.52440734, -4.36373925])

[24]:

lr.intercept_

[24]:

61.05057671902867

On utilise maintenant statsmodels qui est plus complet pour toute ce qui est un modèle linéaire.

[25]:

from statsmodels.formula.api import ols

lr = ols("price ~ age + gender", data=join)
res = lr.fit()
res.summary()

[25]:

OLS Regression Results
Dep. Variable:	price	R-squared:	0.579
Model:	OLS	Adj. R-squared:	0.579
Method:	Least Squares	F-statistic:	686.6
Date:	Thu, 25 Jan 2024	Prob (F-statistic):	3.25e-188
Time:	11:12:30	Log-Likelihood:	-3149.8
No. Observations:	1000	AIC:	6306.
Df Residuals:	997	BIC:	6320.
Df Model:	2
Covariance Type:	nonrobust

	coef	std err	t	P>\|t\|	[0.025	0.975]
Intercept	61.0506	0.640	95.432	0.000	59.795	62.306
age	0.5244	0.015	35.302	0.000	0.495	0.554
gender	-4.3637	0.358	-12.194	0.000	-5.066	-3.662

Omnibus:	300.096	Durbin-Watson:	1.999
Prob(Omnibus):	0.000	Jarque-Bera (JB):	719.506
Skew:	1.618	Prob(JB):	5.77e-157
Kurtosis:	5.608	Cond. No.	151.

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

Ou encore (après avoir ajouté une constante).

[26]:

from statsmodels.api import OLS

join2 = join.copy()
join2["cst"] = 1
lr = OLS(join2["price"], join2[["age", "gender", "cst"]])
res = lr.fit()
res.summary()

[26]:

OLS Regression Results
Dep. Variable:	price	R-squared:	0.579
Model:	OLS	Adj. R-squared:	0.579
Method:	Least Squares	F-statistic:	686.6
Date:	Thu, 25 Jan 2024	Prob (F-statistic):	3.25e-188
Time:	11:12:33	Log-Likelihood:	-3149.8
No. Observations:	1000	AIC:	6306.
Df Residuals:	997	BIC:	6320.
Df Model:	2
Covariance Type:	nonrobust

	coef	std err	t	P>\|t\|	[0.025	0.975]
age	0.5244	0.015	35.302	0.000	0.495	0.554
gender	-4.3637	0.358	-12.194	0.000	-5.066	-3.662
cst	61.0506	0.640	95.432	0.000	59.795	62.306

Omnibus:	300.096	Durbin-Watson:	1.999
Prob(Omnibus):	0.000	Jarque-Bera (JB):	719.506
Skew:	1.618	Prob(JB):	5.77e-157
Kurtosis:	5.608	Cond. No.	151.

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

On peut aussi définir la régression sous la forme de formule avec le module patsy.

[27]:

from patsy import dmatrices

y, X = dmatrices("price ~ age + gender", join, return_type="matrix")
y = numpy.ravel(y)
lr = LinearRegression(fit_intercept=False)
lr.fit(X, y)

[27]:

LinearRegression(fit_intercept=False)

[28]:

lr.coef_, lr.intercept_

[28]:

(array([61.05057672,  0.52440734, -4.36373925]), 0.0)

[29]:

X[:2]

[29]:

array([[ 1., 37.,  0.],
       [ 1., 41.,  0.]])

6¶

On souhaite étudier le prix d’une consultation en fonction du jour de la semaine. Ajouter une colonne dans la table de votre choix avec le jour de la semaine.

On convertit d’abord la colonne date (chaîne de caractères au format date) avec la fonction to_datetime.

[30]:

rend["date2"] = pandas.to_datetime(rend.date)
rend.dtypes

[30]:

date             object
idc              object
idr              object
price           float64
date2    datetime64[ns]
dtype: object

Et on récupère le jour de la semaine avec weekday.

[31]:

rend["weekday"] = rend.date2.dt.weekday
rend.head()

[31]:

	date	idc	idr	price	date2	weekday
0	2016-12-02 19:47:45.068274	4ba0b473-f8ca-4466-a65b-40e9b8ba5029	b7db0ac9-86a1-46f9-98ac-f1f8eb54072d	75.0	2016-12-02 19:47:45.068274	4
1	2016-12-02 19:47:45.068274	4ba0b473-f8ca-4466-a65b-40e9b8ba5029	a65f721a-de11-4a01-be71-b26e2da3ac00	65.0	2016-12-02 19:47:45.068274	4
2	2016-12-07 19:47:45.068274	f44b004b-b01e-4835-b86d-1a42846c6d93	644b1236-b9ee-4ef5-8ca7-d1adadb547c8	75.0	2016-12-07 19:47:45.068274	2
3	2016-12-17 19:47:45.068274	f44b004b-b01e-4835-b86d-1a42846c6d93	aff6ac9e-5dd0-434e-9888-f724f6d40969	80.0	2016-12-17 19:47:45.068274	5
4	2017-01-07 19:47:45.068274	f44b004b-b01e-4835-b86d-1a42846c6d93	9ca87507-aa95-49a9-88b3-86ec9fbc44d6	80.0	2017-01-07 19:47:45.068274	5

7¶

Créer un graphe moustache qui permet de vérifier cette hypothèse.

On réutilise le code d’une question précédente.

[32]:

rend[["price", "weekday"]].boxplot(by="weekday")

[32]:

<Axes: title={'center': 'price'}, xlabel='[weekday]'>

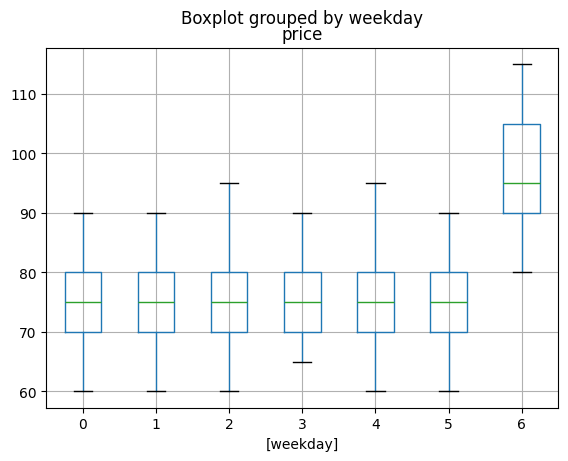
../../_images/practice_exams_enonce_ml_2017_correction_43_1.png

C’est clairement plus cher le dimanche.

8¶

Ajouter une colonne dans la table de votre choix qui contient 365 si c’est le premier rendez-vous, le nombre de jour écoulés depuis le précédent rendez-vous. On appelle cette colonne :math:`delay`. On ajoute également la colonne $1/delay$ .

Pour commencer, on convertit la date en nombre de jours depuis la première date.

[33]:

rend["constant"] = rend["date2"].min()
rend["jour"] = rend["date2"] - rend["constant"]
rend.head(n=2)

[33]:

	date	idc	idr	price	date2	weekday	constant	jour
0	2016-12-02 19:47:45.068274	4ba0b473-f8ca-4466-a65b-40e9b8ba5029	b7db0ac9-86a1-46f9-98ac-f1f8eb54072d	75.0	2016-12-02 19:47:45.068274	4	2016-11-18 19:47:45.068274	14 days
1	2016-12-02 19:47:45.068274	4ba0b473-f8ca-4466-a65b-40e9b8ba5029	a65f721a-de11-4a01-be71-b26e2da3ac00	65.0	2016-12-02 19:47:45.068274	4	2016-11-18 19:47:45.068274	14 days

On convertit en entier.

[34]:

rend["jouri"] = rend.jour.apply(lambda d: d.days)
rend.head(n=2)

[34]:

	date	idc	idr	price	date2	weekday	constant	jour	jouri
0	2016-12-02 19:47:45.068274	4ba0b473-f8ca-4466-a65b-40e9b8ba5029	b7db0ac9-86a1-46f9-98ac-f1f8eb54072d	75.0	2016-12-02 19:47:45.068274	4	2016-11-18 19:47:45.068274	14 days	14
1	2016-12-02 19:47:45.068274	4ba0b473-f8ca-4466-a65b-40e9b8ba5029	a65f721a-de11-4a01-be71-b26e2da3ac00	65.0	2016-12-02 19:47:45.068274	4	2016-11-18 19:47:45.068274	14 days	14

On trie par patient et jour puis on effectue la différence.

[35]:

diff = rend.sort_values(["idc", "jouri"])["jouri"].diff()
rend["diff"] = diff
rend.head(n=2)

[35]:

	date	idc	idr	price	date2	weekday	constant	jour	jouri	diff
0	2016-12-02 19:47:45.068274	4ba0b473-f8ca-4466-a65b-40e9b8ba5029	b7db0ac9-86a1-46f9-98ac-f1f8eb54072d	75.0	2016-12-02 19:47:45.068274	4	2016-11-18 19:47:45.068274	14 days	14	-26.0
1	2016-12-02 19:47:45.068274	4ba0b473-f8ca-4466-a65b-40e9b8ba5029	a65f721a-de11-4a01-be71-b26e2da3ac00	65.0	2016-12-02 19:47:45.068274	4	2016-11-18 19:47:45.068274	14 days	14	0.0

Il reste à traiter le premier jour ou plutôt le premier rendez-vous. On le récupère pour chaque patient.

[36]:

first = rend[["idc", "date"]].groupby("idc", as_index=False).min()
first["j365"] = 365
first.head(n=2)

[36]:

	idc	date	j365
0	003b0195-2acb-4f46-b7fa-28cf266a8f60	2016-12-02 19:47:45.068274	365
1	009e689c-51a1-4cef-99ca-a4ba364eba8d	2016-11-26 19:47:45.068274	365

Puis on fait une jointure.

[37]:

tout = rend.merge(first, on=["idc", "date"], how="outer")
tout[["idc", "jouri", "date", "j365"]].head(n=5)

[37]:

	idc	jouri	date	j365
0	4ba0b473-f8ca-4466-a65b-40e9b8ba5029	14	2016-12-02 19:47:45.068274	365.0
1	4ba0b473-f8ca-4466-a65b-40e9b8ba5029	14	2016-12-02 19:47:45.068274	365.0
2	f44b004b-b01e-4835-b86d-1a42846c6d93	19	2016-12-07 19:47:45.068274	365.0
3	f44b004b-b01e-4835-b86d-1a42846c6d93	29	2016-12-17 19:47:45.068274	NaN
4	f44b004b-b01e-4835-b86d-1a42846c6d93	50	2017-01-07 19:47:45.068274	NaN

Il ne reste plus qu’à remplacer les NaN par jouri.

[38]:

tout["delay"] = tout.j365.fillna(tout.jouri)
tout[["idc", "jouri", "date", "j365", "delay"]].head(n=8)

[38]:

	idc	jouri	date	j365	delay
0	4ba0b473-f8ca-4466-a65b-40e9b8ba5029	14	2016-12-02 19:47:45.068274	365.0	365.0
1	4ba0b473-f8ca-4466-a65b-40e9b8ba5029	14	2016-12-02 19:47:45.068274	365.0	365.0
2	f44b004b-b01e-4835-b86d-1a42846c6d93	19	2016-12-07 19:47:45.068274	365.0	365.0
3	f44b004b-b01e-4835-b86d-1a42846c6d93	29	2016-12-17 19:47:45.068274	NaN	29.0
4	f44b004b-b01e-4835-b86d-1a42846c6d93	50	2017-01-07 19:47:45.068274	NaN	50.0
5	304895f0-f686-4b0e-8854-a705bb5a6982	1	2016-11-19 19:47:45.068274	365.0	365.0
6	3f0d31d2-0ef4-4e7e-b876-07d10225cc8c	30	2016-12-18 19:47:45.068274	365.0	365.0
7	f29273f4-a76c-4158-b5f5-b3e5a080a0c7	2	2016-11-20 19:47:45.068274	365.0	365.0

Finalement, il faut ajouter une colonne $1/delay$ . Comme des patients ont parfois deux rendez-vous le même jour, pour éviter les valeurs nulles, on ajoute la colonne $1/(1+delay)$ . On aurait pu également pour éviter les valeurs nulles considérer le temps en secondes et non en jour entre deux rendez-vous.

[39]:

tout["delay1"] = 1 / (tout["delay"] + 1)
tout[["delay", "delay1"]].head()

[39]:

	delay	delay1
0	365.0	0.002732
1	365.0	0.002732
2	365.0	0.002732
3	29.0	0.033333
4	50.0	0.019608

8 - réponse plus courte¶

On garde l’idée de la fonction diff et on ajoute la fonction shift.

[40]:

rend2 = rend.sort_values(["idc", "jouri"]).reset_index(drop=True).copy()
rend2["diff"] = rend2["jouri"].diff()
rend2.loc[rend2.idc != rend2.idc.shift(1), "diff"] = 365
rend2.head()

[40]:

	date	idc	idr	price	date2	weekday	constant	jour	jouri	diff
0	2016-12-02 19:47:45.068274	003b0195-2acb-4f46-b7fa-28cf266a8f60	6d65b2b5-f34d-4440-8442-679175554db4	80.0	2016-12-02 19:47:45.068274	4	2016-11-18 19:47:45.068274	14 days	14	365.0
1	2016-11-26 19:47:45.068274	009e689c-51a1-4cef-99ca-a4ba364eba8d	065474ed-6ba3-4ee1-aa83-b89e97d5a2aa	80.0	2016-11-26 19:47:45.068274	5	2016-11-18 19:47:45.068274	8 days	8	365.0
2	2016-12-20 19:47:45.068274	009e689c-51a1-4cef-99ca-a4ba364eba8d	38a02a6a-8c04-4630-aaa6-2077077a9f87	80.0	2016-12-20 19:47:45.068274	1	2016-11-18 19:47:45.068274	32 days	32	24.0
3	2017-01-12 19:47:45.068274	009e689c-51a1-4cef-99ca-a4ba364eba8d	f4cf0df4-0b6a-4b0f-93c7-d12499026fab	80.0	2017-01-12 19:47:45.068274	3	2016-11-18 19:47:45.068274	55 days	55	23.0
4	2016-12-02 19:47:45.068274	00a213c2-1174-4359-8a67-fe710ec1b439	c1b3381b-9663-429d-a8fb-3b24c20a125b	70.0	2016-12-02 19:47:45.068274	4	2016-11-18 19:47:45.068274	14 days	14	365.0

9¶

Calculer les coefficients de la régression $prix \sim age + genre + delay + 1/delay + jour\_semaine$ .

L’âge ne fait pas partie de la table tout. Il faut faire une jointure pour le récupérer.

[41]:

mat = tout.merge(persons, on="idc")

Ensuite retour à scikit-learn et plutôt le second statsmodels pour effectuer des tests sur les coefficients du modèle. On regarde d’abord les corrélations.

[42]:

mat[["age", "gender", "delay", "delay1", "weekday", "price"]].corr()

[42]:

	age	gender	delay	delay1	weekday	price
age	1.000000	0.030852	-0.010694	-0.023011	0.032413	0.614708
gender	0.030852	1.000000	0.008700	-0.026779	-0.000064	-0.198835
delay	-0.010694	0.008700	1.000000	-0.616038	0.039766	0.049796
delay1	-0.023011	-0.026779	-0.616038	1.000000	0.025400	-0.054954
weekday	0.032413	-0.000064	0.039766	0.025400	1.000000	0.448584
price	0.614708	-0.198835	0.049796	-0.054954	0.448584	1.000000

[43]:

seaborn.clustermap(
    mat[["age", "gender", "delay", "delay1", "weekday", "price"]].corr(), figsize=(5, 5)
)

[43]:

<seaborn.matrix.ClusterGrid at 0x7fb3214280d0>

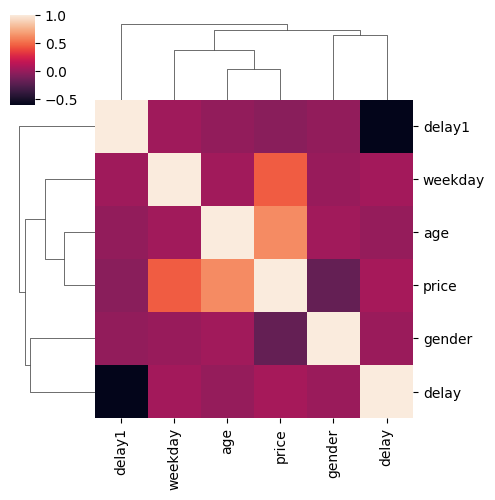
../../_images/practice_exams_enonce_ml_2017_correction_65_1.png

Si le jeu de données n’est pas trop volumineux.

[45]:

seaborn.pairplot(
    mat[["age", "gender", "delay", "delay1", "weekday", "price"]], plot_kws={"s": 10}
)

[45]:

<seaborn.axisgrid.PairGrid at 0x7fb3029bf820>

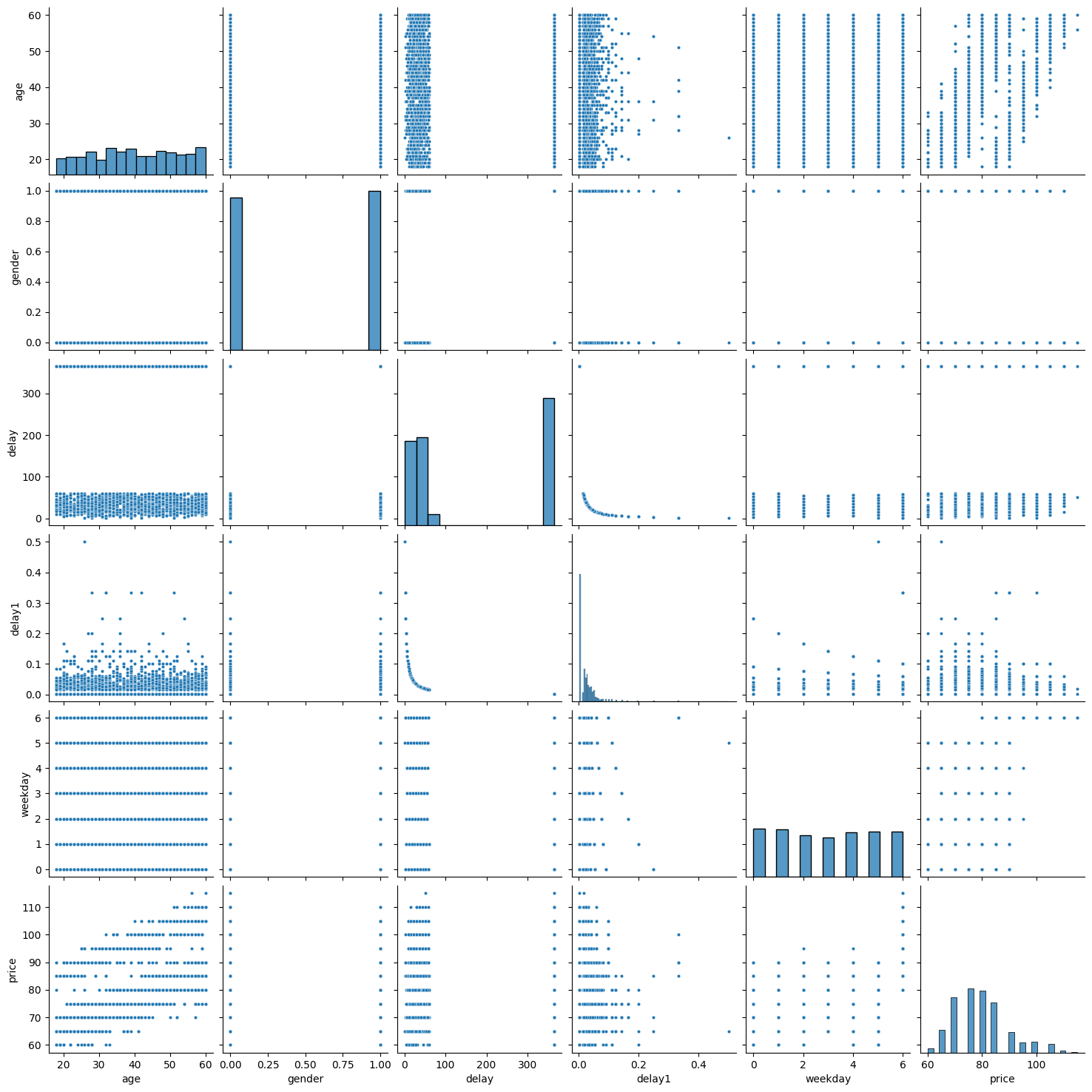
../../_images/practice_exams_enonce_ml_2017_correction_67_2.png

Un dernier pour la route.

[48]:

feat = mat[["age", "gender", "delay", "delay1", "weekday", "price"]]
g = seaborn.PairGrid(
    feat.sort_values("price", ascending=False),
    x_vars=feat.columns[:-1],
    y_vars=["price"],
)
g.map(seaborn.stripplot, size=3, orient="h", palette="Reds_r", edgecolor="gray")

/home/xadupre/.local/lib/python3.10/site-packages/seaborn/_oldcore.py:1119: FutureWarning: use_inf_as_na option is deprecated and will be removed in a future version. Convert inf values to NaN before operating instead.
with pd.option_context('mode.use_inf_as_na', True):
/home/xadupre/.local/lib/python3.10/site-packages/seaborn/_oldcore.py:1119: FutureWarning: use_inf_as_na option is deprecated and will be removed in a future version. Convert inf values to NaN before operating instead.
with pd.option_context('mode.use_inf_as_na', True):
/home/xadupre/.local/lib/python3.10/site-packages/seaborn/_oldcore.py:1119: FutureWarning: use_inf_as_na option is deprecated and will be removed in a future version. Convert inf values to NaN before operating instead.
with pd.option_context('mode.use_inf_as_na', True):
/home/xadupre/.local/lib/python3.10/site-packages/seaborn/_oldcore.py:1119: FutureWarning: use_inf_as_na option is deprecated and will be removed in a future version. Convert inf values to NaN before operating instead.
with pd.option_context('mode.use_inf_as_na', True):
/home/xadupre/.local/lib/python3.10/site-packages/seaborn/_oldcore.py:1119: FutureWarning: use_inf_as_na option is deprecated and will be removed in a future version. Convert inf values to NaN before operating instead.
with pd.option_context('mode.use_inf_as_na', True):
/home/xadupre/.local/lib/python3.10/site-packages/seaborn/_oldcore.py:1119: FutureWarning: use_inf_as_na option is deprecated and will be removed in a future version. Convert inf values to NaN before operating instead.
with pd.option_context('mode.use_inf_as_na', True):
/home/xadupre/.local/lib/python3.10/site-packages/seaborn/_oldcore.py:1119: FutureWarning: use_inf_as_na option is deprecated and will be removed in a future version. Convert inf values to NaN before operating instead.
with pd.option_context('mode.use_inf_as_na', True):
/home/xadupre/.local/lib/python3.10/site-packages/seaborn/_oldcore.py:1119: FutureWarning: use_inf_as_na option is deprecated and will be removed in a future version. Convert inf values to NaN before operating instead.
with pd.option_context('mode.use_inf_as_na', True):
/home/xadupre/.local/lib/python3.10/site-packages/seaborn/_oldcore.py:1119: FutureWarning: use_inf_as_na option is deprecated and will be removed in a future version. Convert inf values to NaN before operating instead.
with pd.option_context('mode.use_inf_as_na', True):
/home/xadupre/.local/lib/python3.10/site-packages/seaborn/_oldcore.py:1119: FutureWarning: use_inf_as_na option is deprecated and will be removed in a future version. Convert inf values to NaN before operating instead.
with pd.option_context('mode.use_inf_as_na', True):

[48]:

<seaborn.axisgrid.PairGrid at 0x7fb2fad7ac20>

../../_images/practice_exams_enonce_ml_2017_correction_69_2.png

Régression

[49]:

lr = LinearRegression()
lr.fit(mat[["age", "gender", "delay", "delay1", "weekday"]], mat["price"])
lr.coef_

[49]:

array([ 5.08109837e-01, -4.41245429e+00,  5.42852787e-04, -1.60797483e+01,
        2.12155016e+00])

[50]:

from statsmodels.formula.api import ols

lr = ols("price ~ age + gender + delay + delay1 + weekday", data=mat)
res = lr.fit()
res.summary()

[50]:

OLS Regression Results
Dep. Variable:	price	R-squared:	0.612
Model:	OLS	Adj. R-squared:	0.612
Method:	Least Squares	F-statistic:	800.0
Date:	Thu, 25 Jan 2024	Prob (F-statistic):	0.00
Time:	11:15:05	Log-Likelihood:	-8257.2
No. Observations:	2537	AIC:	1.653e+04
Df Residuals:	2531	BIC:	1.656e+04
Df Model:	5
Covariance Type:	nonrobust

	coef	std err	t	P>\|t\|	[0.025	0.975]
Intercept	55.4146	0.545	101.618	0.000	54.345	56.484
age	0.5081	0.010	48.918	0.000	0.488	0.528
gender	-4.4125	0.250	-17.683	0.000	-4.902	-3.923
delay	0.0005	0.001	0.562	0.574	-0.001	0.002
delay1	-16.0797	4.842	-3.321	0.001	-25.575	-6.585
weekday	2.1216	0.061	34.623	0.000	2.001	2.242

Omnibus:	55.147	Durbin-Watson:	1.969
Prob(Omnibus):	0.000	Jarque-Bera (JB):	57.558
Skew:	0.358	Prob(JB):	3.17e-13
Kurtosis:	2.823	Cond. No.	9.20e+03

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 9.2e+03. This might indicate that there are
strong multicollinearity or other numerical problems.

10¶

Comment comparer ce modèle avec le précédent ? Implémentez le calcul qui vous permet de répondre à cette question.

Nous pourrions comparer les coefficients $R^2$ (0.57, 0.61) des régressions pour savoir quelle est la meilleur excepté que celle-ci ne sont pas calculées sur les mêmes données. La comparaison n’a pas de sens et il serait dangeraux d’en tirer des conclusions. Les valeurs sont de plus très proches. Il faut comparer les prédictions. Dans le premier cas, on prédit le prix moyen. Dans le second, on prédit le prix d’une consultation. Il est alors possible de calculer une prédiction moyenne par patient et de comparer les erreurs de prédiction du prix moyen. D’un côté, la prédiction du prix moyen, de l’autre la prédiction du prix d’une consultation agrégé par patient.

[51]:

lr_moy = LinearRegression()
lr_moy.fit(join[["age", "gender"]], join["price"])
lr_moy.coef_, lr_moy.intercept_

[51]:

(array([ 0.52440734, -4.36373925]), 61.05057671902867)

[52]:

pred_moy = lr_moy.predict(join[["age", "gender"]])
join["pred_moy"] = pred_moy
join.head()

[52]:

	age	gender	idc	name	price	pred_moy
0	37	0	4ba0b473-f8ca-4466-a65b-40e9b8ba5029	Cendrillon	70.000000	80.453648
1	41	0	f44b004b-b01e-4835-b86d-1a42846c6d93	Cendrillon	78.333333	82.551278
2	46	1	304895f0-f686-4b0e-8854-a705bb5a6982	Balthazar	75.000000	80.809575
3	42	1	3f0d31d2-0ef4-4e7e-b876-07d10225cc8c	Balthazar	95.000000	78.711946
4	41	1	f29273f4-a76c-4158-b5f5-b3e5a080a0c7	Balthazar	90.000000	78.187538

On calcule l’erreur.

[53]:

err1 = ((join.pred_moy - join.price) ** 2).sum() / join.shape[0]
err1

[53]:

31.874448844571756

[54]:

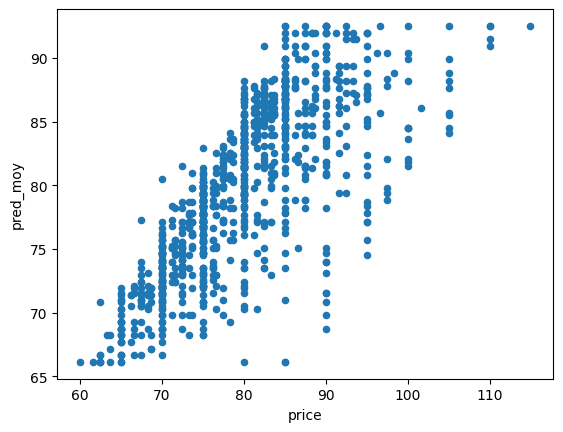
join.plot(x="price", y="pred_moy", kind="scatter")

[54]:

<Axes: xlabel='price', ylabel='pred_moy'>

../../_images/practice_exams_enonce_ml_2017_correction_78_1.png

[55]:

lrc = LinearRegression()
feat = mat[["age", "gender", "delay", "delay1", "weekday", "price", "idc"]].copy()
lrc.fit(feat[["age", "gender", "delay", "delay1", "weekday"]], feat["price"])
lrc.coef_, lrc.intercept_

[55]:

(array([ 5.08109837e-01, -4.41245429e+00,  5.42852787e-04, -1.60797483e+01,
         2.12155016e+00]),
 55.41460950333407)

[56]:

predc = lrc.predict(feat[["age", "gender", "delay", "delay1", "weekday"]])
feat["predc"] = predc
feat.head()

[56]:

	age	delay	delay1	weekday	price	idc	predc
0	37	365.0	0.002732	4	75.0	4ba0b473-f8ca-4466-a65b-40e9b8ba5029	82.855082
1	37	365.0	0.002732	4	65.0	4ba0b473-f8ca-4466-a65b-40e9b8ba5029	82.855082
2	41	365.0	0.002732	2	75.0	f44b004b-b01e-4835-b86d-1a42846c6d93	80.644421
3	41	29.0	0.033333	5	80.0	f44b004b-b01e-4835-b86d-1a42846c6d93	86.334615
4	41	50.0	0.019608	5	80.0	f44b004b-b01e-4835-b86d-1a42846c6d93	86.566717

On agrège les secondes prédictions.

[57]:

agg = feat[["idc", "predc", "price"]].groupby("idc").mean()
agg.head()

[57]:

	predc	price
idc
003b0195-2acb-4f46-b7fa-28cf266a8f60	85.048055	80.0
009e689c-51a1-4cef-99ca-a4ba364eba8d	83.945104	80.0
00a213c2-1174-4359-8a67-fe710ec1b439	72.345309	70.0
00e42818-aade-4758-a5f6-c78a6f235ea5	65.277461	70.0
0153b785-9acd-4d28-aad1-62f8bf2faea3	79.298313	75.0

[58]:

err2 = ((agg.predc - agg.price) ** 2).sum() / agg.shape[0]
err2

[58]:

20.697836056479865

Le second modèle est clairement meilleur.

[59]:

agg.plot(x="price", y="predc", kind="scatter")

[59]:

<Axes: xlabel='price', ylabel='predc'>

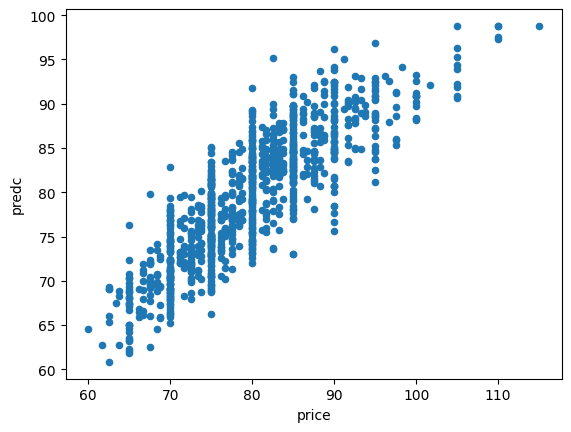
../../_images/practice_exams_enonce_ml_2017_correction_85_1.png

La seconde régression utilise une information dont on ne dispose pas au niveau agrégé : le jour de la semaine et un précédent graphe a clairement montré que c’était une variable importante. Un dernier graphe pour comparer les deux prédictions en montrant les prédictions triées par prix à prédire.

[60]:

temp = join.sort_values("price").reset_index(drop=True).reset_index(drop=False)
temp.head(n=1)

[60]:

	index	age	gender	idc	name	price	pred_moy
0	0	18	1	6423a722-4769-4a7c-8d1d-266538c2a07a	Balthazar	60.0	66.12617

[61]:

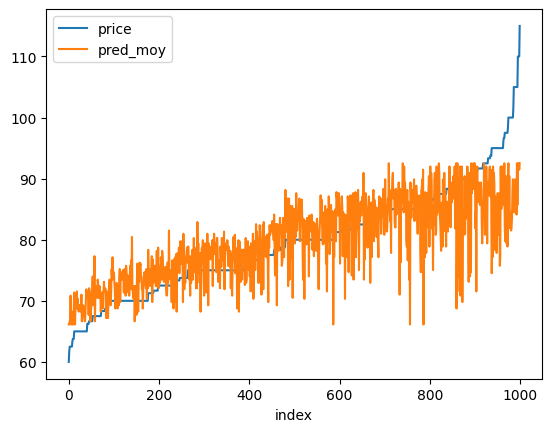
temp.plot(x="index", y=["price", "pred_moy"])

[61]:

<Axes: xlabel='index'>

../../_images/practice_exams_enonce_ml_2017_correction_88_1.png

[62]:

temp2 = agg.sort_values("price").reset_index(drop=True).reset_index(drop=False)
temp2.head(n=1)

[62]:

	index	predc	price
0	0	64.54544	60.0

[63]:

ax = temp.plot(x="index", y="price", figsize=(14, 4), ylim=[60, 120])
temp.plot(x="index", y="pred_moy", linewidth=1, ax=ax, ylim=[60, 120])
temp2.plot(x="index", y="predc", ax=ax, linewidth=0.6, ylim=[60, 120])

[63]:

<Axes: xlabel='index'>

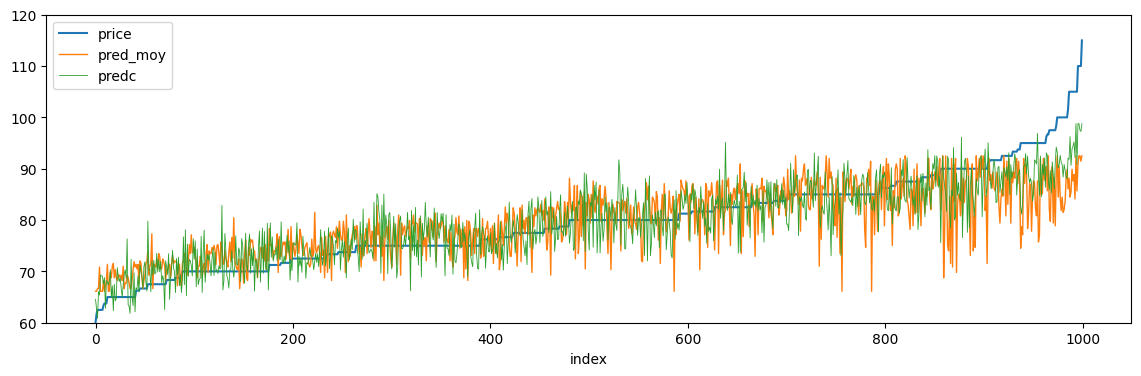
../../_images/practice_exams_enonce_ml_2017_correction_90_1.png

C’est finalement un peu plus visible sur le graphe précédent (nuage de points) mais aussi un peu trompeur du fait de la superposition des points. Une dernière remarque. En machine learning, nous avons l’habitude d’apprendre un modèle sur une base d’apprentissage et de tester les prédictions sur une autre. Dans notre cas, nous avons appris et prédit sur la même base. Ce type de tester est évidemment plus fiable. Mais nous avons comparé ici deux erreurs d’apprentissage moyennes et c’est exactement ce que l’on fait lorsqu’on compare deux coefficients $R^2$ .

Un dernier graphe pour la route obtenu en triant les erreurs par ordre croissant.

[64]:

temp["erreur"] = temp.pred_moy - temp.price
temp2["erreur2"] = temp2.predc - temp2.price
ax = temp[["erreur"]].sort_values("erreur").reset_index(drop=True).plot()
temp2[["erreur2"]].sort_values("erreur2").reset_index(drop=True).plot(ax=ax)
ax.plot([0, 1000], [0, 0], "r--")

[64]:

[<matplotlib.lines.Line2D at 0x7fb2fa805210>]

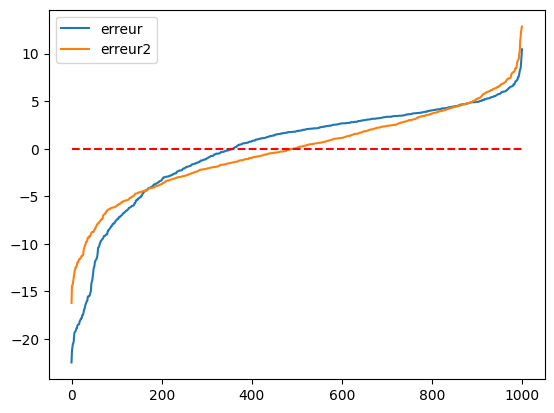
../../_images/practice_exams_enonce_ml_2017_correction_92_1.png

Le second modèle fait des erreurs moins importantes surtout côté négatif. Il sous-estime moins la bonne valeur.

Traitement spécifique de la variable catégorielle weekday¶

Le second modèle ne prend pas en compte le dimanche comme jour de la semaine. weekday est une variable catégorielle. Contrairment au genre, elle possède plus de deux modalités. Il serait intéressant de la traiter comme un ensemble de variable binaire et non une colonne de type entier.

[65]:

dummies = pandas.get_dummies(mat.weekday)
dummies.columns = ["lu", "ma", "me", "je", "ve", "sa", "di"]
dummies.head()

[65]:

	lu	ma	me	je	ve	sa	di
0	False	False	False	False	True	False	False
1	False	False	False	False	True	False	False
2	False	False	True	False	False	False	False
3	False	False	False	False	False	True	False
4	False	False	False	False	False	True	False

On supprime une modalité pour éviter d’avoir une matrice corrélée avec la constante et on ajoute des variables au modèle de régression.

[66]:

mat2 = pandas.concat([mat, dummies.drop("lu", axis=1)], axis=1)
mat2.head(n=1)

[66]:

	date	idc	idr	price	date2	weekday	constant	jour	jouri	diff	...	delay1	age	gender	name	ma	me	je	ve	sa	di
0	2016-12-02 19:47:45.068274	4ba0b473-f8ca-4466-a65b-40e9b8ba5029	b7db0ac9-86a1-46f9-98ac-f1f8eb54072d	75.0	2016-12-02 19:47:45.068274	4	2016-11-18 19:47:45.068274	14 days	14	-26.0	...	0.002732	37	0	Cendrillon	False	False	False	True	False	False

1 rows × 22 columns

[67]:

lr = ols(
    "price ~ age + gender + delay + delay1 + ma + me + je + ve + sa + di", data=mat2
)
res = lr.fit()
res.summary()

[67]:

OLS Regression Results
Dep. Variable:	price	R-squared:	0.918
Model:	OLS	Adj. R-squared:	0.917
Method:	Least Squares	F-statistic:	2812.
Date:	Thu, 25 Jan 2024	Prob (F-statistic):	0.00
Time:	11:15:41	Log-Likelihood:	-6293.7
No. Observations:	2537	AIC:	1.261e+04
Df Residuals:	2526	BIC:	1.267e+04
Df Model:	10
Covariance Type:	nonrobust

	coef	std err	t	P>\|t\|	[0.025	0.975]
Intercept	59.0371	0.272	217.342	0.000	58.504	59.570
ma[T.True]	-0.0840	0.208	-0.405	0.686	-0.491	0.323
me[T.True]	0.3003	0.216	1.392	0.164	-0.123	0.723
je[T.True]	0.1607	0.219	0.735	0.463	-0.268	0.590
ve[T.True]	-0.1748	0.212	-0.825	0.409	-0.590	0.240
sa[T.True]	0.1849	0.210	0.879	0.379	-0.227	0.597
di[T.True]	20.0978	0.211	95.203	0.000	19.684	20.512
age	0.5005	0.005	104.318	0.000	0.491	0.510
gender	-4.0722	0.115	-35.321	0.000	-4.298	-3.846
delay	0.0003	0.000	0.661	0.509	-0.001	0.001
delay1	-20.7385	2.236	-9.275	0.000	-25.123	-16.354

Omnibus:	257.849	Durbin-Watson:	2.034
Prob(Omnibus):	0.000	Jarque-Bera (JB):	484.437
Skew:	-0.672	Prob(JB):	6.40e-106
Kurtosis:	4.666	Cond. No.	9.20e+03

On vérifie que le coefficient pour dimanche n’est clairement significatif contrairement aux autres dont la probabilité d’être nul est élevée. Le médecin appliquerait une majoration de 20 euros le dimanche. Le coefficient $R^2$ est aussi nettement plus élevé. On construit les prédictions d’un second modèle en ne tenant compte que de la variable dimanche.

[68]:

lrc = LinearRegression()
feat2 = mat2[["age", "gender", "delay", "delay1", "price", "idc", "di"]].copy()
lrc.fit(feat2[["age", "gender", "delay", "delay1", "di"]], feat2["price"])
lrc.coef_, lrc.intercept_

[68]:

(array([ 5.00892234e-01, -4.07229120e+00,  2.97614199e-04, -2.07004497e+01,
         2.00395644e+01]),
 59.07951294272968)

[69]:

predc = lrc.predict(feat2[["age", "gender", "delay", "delay1", "di"]])
feat2["predc"] = predc
feat2.head()

[69]:

	age	delay	delay1	price	idc	di	predc
0	37	365.0	0.002732	75.0	4ba0b473-f8ca-4466-a65b-40e9b8ba5029	False	77.664596
1	37	365.0	0.002732	65.0	4ba0b473-f8ca-4466-a65b-40e9b8ba5029	False	77.664596
2	41	365.0	0.002732	75.0	f44b004b-b01e-4835-b86d-1a42846c6d93	False	79.668165
3	41	29.0	0.033333	80.0	f44b004b-b01e-4835-b86d-1a42846c6d93	False	78.934710
4	41	50.0	0.019608	80.0	f44b004b-b01e-4835-b86d-1a42846c6d93	False	79.225084

[70]:

agg2 = feat2[["idc", "predc", "price"]].groupby("idc").mean()
agg2.head()

[70]:

	predc	price
idc
003b0195-2acb-4f46-b7fa-28cf266a8f60	80.103904	80.0
009e689c-51a1-4cef-99ca-a4ba364eba8d	80.812446	80.0
00a213c2-1174-4359-8a67-fe710ec1b439	67.581598	70.0
00e42818-aade-4758-a5f6-c78a6f235ea5	66.890947	70.0
0153b785-9acd-4d28-aad1-62f8bf2faea3	74.158351	75.0

[71]:

err2d = ((agg2.predc - agg2.price) ** 2).sum() / agg2.shape[0]
err2d

[71]:

3.626505427547838

Nettement, nettement mieux.

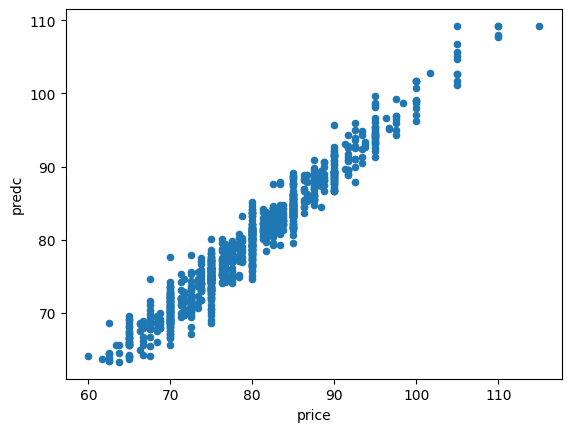
[72]:

agg2.plot(x="price", y="predc", kind="scatter")

[72]:

<Axes: xlabel='price', ylabel='predc'>

../../_images/practice_exams_enonce_ml_2017_correction_105_1.png

[73]:

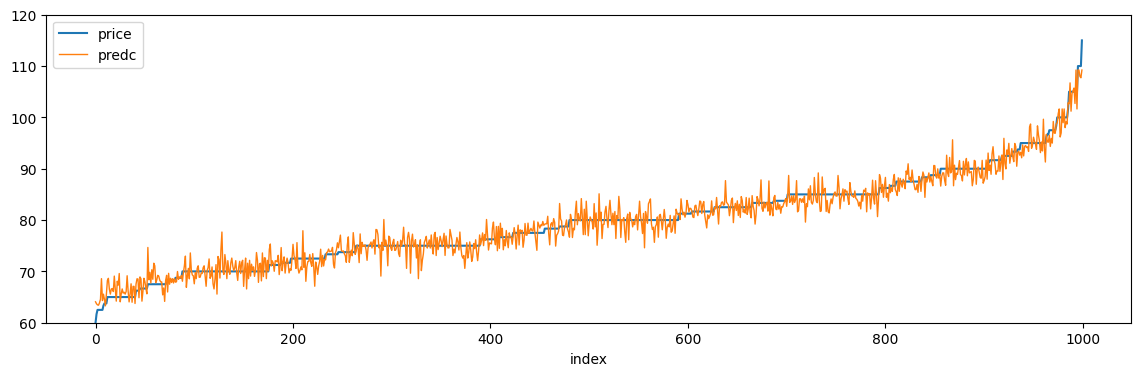
temp2 = agg2.sort_values("price").reset_index(drop=True).reset_index(drop=False)
ax = temp2.plot(x="index", y="price", figsize=(14, 4), ylim=[60, 120])
temp2.plot(x="index", y="predc", linewidth=1, ax=ax, ylim=[60, 120])

[73]:

<Axes: xlabel='index'>

../../_images/practice_exams_enonce_ml_2017_correction_106_1.png

Une variable catégorielle en une seule colonne ?¶

Un jeu de données peut rapidement croître s’il est étendu pour chaque variable catégorielle. On peut utiliser le module category_encoders ou statsmodels.

[74]:

from category_encoders import PolynomialEncoder

encoder = PolynomialEncoder(cols=["weekday"])
encoder.fit(rend[["weekday"]], rend["price"])
pred = encoder.transform(rend[["weekday"]])
conc = pandas.concat([rend[["weekday"]], pred], axis=1)
conc.head()

/home/xadupre/.local/lib/python3.10/site-packages/category_encoders/base_contrast_encoder.py:126: FutureWarning: Intercept column might not be added anymore in future releases (c.f. issue #370)
  warnings.warn("Intercept column might not be added anymore in future releases (c.f. issue #370)",
/home/xadupre/.local/lib/python3.10/site-packages/category_encoders/base_contrast_encoder.py:126: FutureWarning: Intercept column might not be added anymore in future releases (c.f. issue #370)
  warnings.warn("Intercept column might not be added anymore in future releases (c.f. issue #370)",

[74]:

	weekday	intercept	weekday_0	weekday_1	weekday_2	weekday_3	weekday_4	weekday_5
0	4	1	-0.566947	0.545545	-0.408248	0.241747	-0.109109	0.032898
1	4	1	-0.566947	0.545545	-0.408248	0.241747	-0.109109	0.032898
2	2	1	-0.377964	0.000000	0.408248	-0.564076	0.436436	-0.197386
3	5	1	-0.188982	-0.327327	0.408248	0.080582	-0.545545	0.493464
4	5	1	-0.188982	-0.327327	0.408248	0.080582	-0.545545	0.493464

Ou associer la valeur de la cible à prédire pour chaque jour de la semaine.

[75]:

copy = rend[["weekday", "price"]].copy()
gr = copy.groupby("weekday", as_index=False).mean()
gr

[75]:

	weekday	price
0	0	76.112532
1	1	76.195373
2	2	77.047478
3	3	76.677116
4	4	76.049724
5	5	76.630728
6	6	97.078804

[76]:

feat3 = mat[["age", "gender", "delay", "delay1", "price", "idc", "weekday"]]
feat3 = feat3.merge(gr, on="weekday", suffixes=("", "_label"))
feat3.head()

[76]:

	age	gender	delay	delay1	price	idc	weekday	price_label
0	37	0	365.0	0.002732	75.0	4ba0b473-f8ca-4466-a65b-40e9b8ba5029	4	76.049724
1	37	0	365.0	0.002732	65.0	4ba0b473-f8ca-4466-a65b-40e9b8ba5029	4	76.049724
2	57	1	365.0	0.002732	85.0	7ffb8a8b-a829-41f1-9572-2985ee9ba05e	4	76.049724
3	30	0	365.0	0.002732	75.0	0153b785-9acd-4d28-aad1-62f8bf2faea3	4	76.049724
4	28	1	28.0	0.034483	70.0	47e415f0-f4e9-40c5-a59d-adc4c0621c8a	4	76.049724

On apprend avec la variable weekday :

[77]:

lr = ols("price ~ age + gender + delay + delay1 + weekday", data=feat3)
res = lr.fit()
res.summary()

[77]:

OLS Regression Results
Dep. Variable:	price	R-squared:	0.612
Model:	OLS	Adj. R-squared:	0.612
Method:	Least Squares	F-statistic:	800.0
Date:	Thu, 25 Jan 2024	Prob (F-statistic):	0.00
Time:	11:15:56	Log-Likelihood:	-8257.2
No. Observations:	2537	AIC:	1.653e+04
Df Residuals:	2531	BIC:	1.656e+04
Df Model:	5
Covariance Type:	nonrobust

	coef	std err	t	P>\|t\|	[0.025	0.975]
Intercept	55.4146	0.545	101.618	0.000	54.345	56.484
age	0.5081	0.010	48.918	0.000	0.488	0.528
gender	-4.4125	0.250	-17.683	0.000	-4.902	-3.923
delay	0.0005	0.001	0.562	0.574	-0.001	0.002
delay1	-16.0797	4.842	-3.321	0.001	-25.575	-6.585
weekday	2.1216	0.061	34.623	0.000	2.001	2.242

Omnibus:	55.147	Durbin-Watson:	0.442
Prob(Omnibus):	0.000	Jarque-Bera (JB):	57.558
Skew:	0.358	Prob(JB):	3.17e-13
Kurtosis:	2.823	Cond. No.	9.20e+03

Et on compare avec la variable price_label :

[78]:

lr = ols("price ~ age + gender + delay + delay1 + price_label", data=feat3)
res = lr.fit()
res.summary()

[78]:

OLS Regression Results
Dep. Variable:	price	R-squared:	0.917
Model:	OLS	Adj. R-squared:	0.917
Method:	Least Squares	F-statistic:	5611.
Date:	Thu, 25 Jan 2024	Prob (F-statistic):	0.00
Time:	11:15:58	Log-Likelihood:	-6298.8
No. Observations:	2537	AIC:	1.261e+04
Df Residuals:	2531	BIC:	1.264e+04
Df Model:	5
Covariance Type:	nonrobust

	coef	std err	t	P>\|t\|	[0.025	0.975]
Intercept	-14.9859	0.664	-22.576	0.000	-16.288	-13.684
age	0.5000	0.005	104.173	0.000	0.491	0.509
gender	-4.0767	0.115	-35.344	0.000	-4.303	-3.851
delay	0.0003	0.000	0.601	0.548	-0.001	0.001
delay1	-20.8060	2.237	-9.303	0.000	-25.192	-16.420
price_label	0.9696	0.008	122.209	0.000	0.954	0.985

Omnibus:	249.245	Durbin-Watson:	2.035
Prob(Omnibus):	0.000	Jarque-Bera (JB):	459.156
Skew:	-0.660	Prob(JB):	1.98e-100
Kurtosis:	4.613	Cond. No.	9.47e+03

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 9.47e+03. This might indicate that there are
strong multicollinearity or other numerical problems.

Aussi bien qu’avec la variable dimanche.

Notebook on github