Régression linéaire¶

Ce notebook s’intéresse à la façon d’interpréter les résultats d’une régression linéaire lorsque les variables sont corrélées puis il explore une façon d’associer arbre de décision et régression linéaire pour construire une régression linéaire par morceaux.

[11]:

%matplotlib inline

Un cas simple¶

Une façon d’interpréter des résultats statistiques est de les calculer dans un cas où la réponse cherchée est connue. On simule un modèle simple $Y=\alpha X_1 + 0.X_2 + \epsilon$ et on cale une régression linéaire. On suppose que $X_1, X_2, \epsilon$ sont des variables aléatoires gaussiennes de même variance et moyenne.

[12]:

import numpy.random as npr

eps = npr.normal(1000)
X = npr.normal(size=(1000, 3))
alpha = 2
Y = alpha * X[:, 0] + X[:, 2]
X.shape, Y.shape

[12]:

((1000, 3), (1000,))

[13]:

from numpy import corrcoef

corrcoef(X.T)

[13]:

array([[ 1.        ,  0.02585011, -0.00808406],
       [ 0.02585011,  1.        ,  0.00338766],
       [-0.00808406,  0.00338766,  1.        ]])

[14]:

from statsmodels.regression.linear_model import OLS

[15]:

model = OLS(Y, X[:, :2])
results = model.fit()
su = results.summary()
su

[15]:

OLS Regression Results
Dep. Variable:	y	R-squared (uncentered):	0.803
Model:	OLS	Adj. R-squared (uncentered):	0.802
Method:	Least Squares	F-statistic:	2029.
Date:	Mon, 07 Oct 2024	Prob (F-statistic):	0.00
Time:	11:29:03	Log-Likelihood:	-1417.8
No. Observations:	1000	AIC:	2840.
Df Residuals:	998	BIC:	2849.
Df Model:	2
Covariance Type:	nonrobust

	coef	std err	t	P>\|t\|	[0.025	0.975]
x1	1.9922	0.031	63.680	0.000	1.931	2.054
x2	0.0041	0.032	0.130	0.896	-0.058	0.067

Omnibus:	4.685	Durbin-Watson:	2.126
Prob(Omnibus):	0.096	Jarque-Bera (JB):	4.706
Skew:	-0.167	Prob(JB):	0.0951
Kurtosis:	2.972	Cond. No.	1.03

Notes:
[1] R² is computed without centering (uncentered) since the model does not contain a constant.
[2] Standard Errors assume that the covariance matrix of the errors is correctly specified.

[16]:

results.rsquared, results.rsquared_adj

[16]:

(np.float64(0.8026213180783517), np.float64(0.8022257696175868))

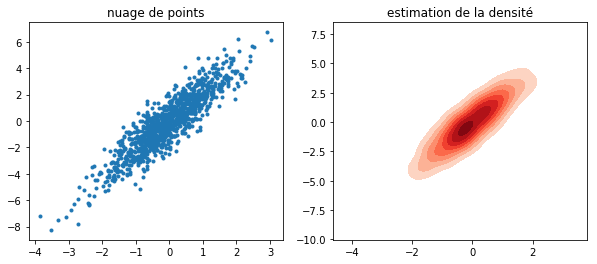
On vérifie que le coefficient devant $X_1$ est non nul (P-value nulle, 0 n’est pas l’intervalle de confiance). Le coefficient devant $X_2$ n’est pas nul mais presque, la P-value est élevée, le coefficient $R^2$ est élevé. Dessinons.

[17]:

import matplotlib.pyplot as plt
import seaborn

fig, ax = plt.subplots(1, 2, figsize=(10, 4))
ax[0].plot(X[:, 0], Y, ".")
seaborn.kdeplot(x=X[:, 0], y=Y, cmap="Reds", shade=True, shade_lowest=False, ax=ax[1])
ax[0].set_title("nuage de points")
ax[1].set_title("estimation de la densité");

/tmp/ipykernel_21413/1827909711.py:6: UserWarning:

`shade_lowest` has been replaced by `thresh`; setting `thresh=0.05.
This will become an error in seaborn v0.14.0; please update your code.

  seaborn.kdeplot(x=X[:, 0], y=Y, cmap="Reds", shade=True, shade_lowest=False, ax=ax[1])
/tmp/ipykernel_21413/1827909711.py:6: FutureWarning:

`shade` is now deprecated in favor of `fill`; setting `fill=True`.
This will become an error in seaborn v0.14.0; please update your code.

  seaborn.kdeplot(x=X[:, 0], y=Y, cmap="Reds", shade=True, shade_lowest=False, ax=ax[1])

../../_images/notebooks_dsgarden_regression_lineaire_9_1.png

Evolution de R2¶

Dans la régression précédente, le coefficient $R^2$ transcrit en quelque sorte la part du bruit $\epsilon$ par rapport au terme $\alpha X_1$ . Faisons varier $\alpha$ .

[18]:

alphas = []
r2s = []
for a in [0.1 * i for i in range(50)]:
    Y = a * X[:, 0] + X[:, 2]
    model = OLS(Y, X[:, :2])
    results = model.fit()
    alphas.append(a)
    r2s.append(results.rsquared)

[19]:

fig, ax = plt.subplots(1, 1)
ax.plot(alphas, r2s, ".", label="observed")
ax.plot(alphas, [a**2 / (1 + a**2) for a in alphas], label="theoretical")
ax.set_xlabel("alpha")
ax.set_ylabel("r2")
ax.legend();

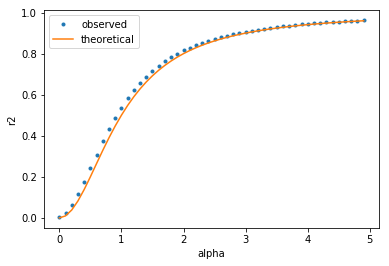
../../_images/notebooks_dsgarden_regression_lineaire_12_0.png

Dans ce cas de régression simple, la valeur à prédire est $y_i$ , la valeur prédite est $\hat{y_i}=\alpha X_{1i}$ et la moyenne $\bar{y} = \alpha \bar{X_1} + \bar{\epsilon} = 0$ .

$R^2 = 1 - \frac{\sum_{i=1}^n (\hat{y_i}-\bar{y})^2}{\sum_{i=1}^n (y_i - \bar{y})^2}=1-\frac{\mathbb{V}\epsilon}{\alpha^2\mathbb{V}X_1+\mathbb{V}\epsilon} = 1 - \frac{1}{1+\alpha^2}=\frac{\alpha^2}{1+\alpha^2}$

Deux variables corrélées¶

On ne change pas le modèle mais on fait en sorte que $X_2=X_1$ . Les deux variables sont corrélées.

[20]:

X[:, 1] = X[:, 0]
Y = 2 * X[:, 0] + X[:, 2]
model = OLS(Y, X[:, :2])
results = model.fit()
results.summary()

[20]:

OLS Regression Results
Dep. Variable:	y	R-squared (uncentered):	0.803
Model:	OLS	Adj. R-squared (uncentered):	0.802
Method:	Least Squares	F-statistic:	4062.
Date:	Mon, 07 Oct 2024	Prob (F-statistic):	0.00
Time:	11:29:04	Log-Likelihood:	-1417.8
No. Observations:	1000	AIC:	2838.
Df Residuals:	999	BIC:	2843.
Df Model:	1
Covariance Type:	nonrobust

	coef	std err	t	P>\|t\|	[0.025	0.975]
x1	0.9961	0.016	63.736	0.000	0.965	1.027
x2	0.9961	0.016	63.736	0.000	0.965	1.027

Omnibus:	4.681	Durbin-Watson:	2.126
Prob(Omnibus):	0.096	Jarque-Bera (JB):	4.705
Skew:	-0.167	Prob(JB):	0.0951
Kurtosis:	2.971	Cond. No.	3.15e+16

Notes:
[1] R² is computed without centering (uncentered) since the model does not contain a constant.
[2] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[3] The smallest eigenvalue is 2.06e-30. This might indicate that there are
strong multicollinearity problems or that the design matrix is singular.

[21]:

model.rank

[21]:

np.int64(1)

Les variables corrélées n’ont pas l’air de déranger l’algorithme de résolution car il utilise la méthode SVD pour résoudre le même problème dans un espace de moindre dimension. Le problème survient que les deux variables ne sont pas complétement corrélées. On étudie le modèle $Y \sim X_1 + X'_2$ avec $X'_2 = \alpha X_1 + (1-\alpha) X_2$ et on réduit la variance du bruit pour en diminuer les effets.

[22]:

X_ = npr.normal(size=(1000, 3))

[23]:

alphas = [0.9 + i * 0.01 for i in range(11)]
res = []
for a in alphas:
    X = X_.copy()
    X[:, 1] = a * X[:, 0] + (1 - a) * X[:, 1]
    Y = X[:, 0] + X[:, 1] + 0.1 * X[:, 2]
    model = OLS(Y, X[:, :2])
    results = model.fit()
    res.append(
        dict(
            alpha=a,
            r2=results.rsquared,
            rank=model.rank,
            c1=results.params[0],
            c2=results.params[1],
        )
    )

import pandas

df = pandas.DataFrame(res)
df = df.set_index("alpha")
df

[23]:

	r2	rank	c1	c2
alpha
0.90	0.997328	2	1.013974	0.986445
0.91	0.997353	2	1.015480	0.984939
0.92	0.997379	2	1.017363	0.983056
0.93	0.997403	2	1.019783	0.980636
0.94	0.997428	2	1.023011	0.977409
0.95	0.997453	2	1.027529	0.972890
0.96	0.997477	2	1.034306	0.966113
0.97	0.997501	2	1.045602	0.954817
0.98	0.997525	2	1.068193	0.932226
0.99	0.997548	2	1.135968	0.864452
1.00	0.997571	1	1.000861	1.000861

[24]:

fig, ax = plt.subplots(1, 2, figsize=(10, 4))
df[["r2"]].plot(ax=ax[0])
df[["c1", "c2"]].plot(ax=ax[1])
ax[0].set_title("R2")
ax[1].set_title("coefficients");

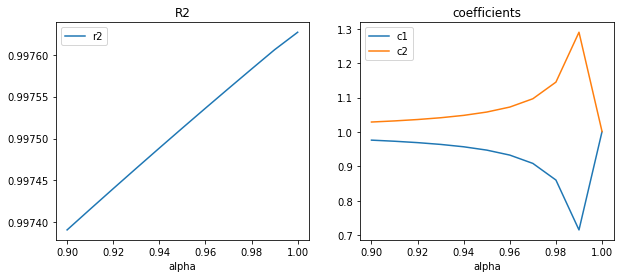
../../_images/notebooks_dsgarden_regression_lineaire_20_0.png

Le $r^2$ augmente quand la corrélation augmente mais les coefficients sont moins fiables. Les résultats devraient être sensiblement identiques en théorie mais en pratique, plus le déterminant devient proche de zéro, plus l’ordinateur est limité par sa précision numérique. Pour en savoir plus, vous pouvez lire un examen écrit que j’ai rédigé, en python bien sûr : Examen Programmation ENSAE première année 2006. Cette précision est aux alentours de $10^{-15}$ ce qui correspond à la précision numérique des double.

[25]:

alphas = [1 - 10 ** (-i) for i in range(10, 18)]
res = []
for a in alphas:
    X = X_.copy()
    X[:, 1] = a * X[:, 0] + (1 - a) * X[:, 1]
    Y = X[:, 0] + X[:, 1] + X[:, 2]
    model = OLS(Y, X[:, :2])
    results = model.fit()
    res.append(
        dict(
            alpha_1=a - 1,
            r2=results.rsquared,
            rank=model.rank,
            c1=results.params[0],
            c2=results.params[1],
        )
    )

import pandas

df = pandas.DataFrame(res)
df = df.set_index("alpha_1")
df

[25]:

	r2	rank	c1	c2
alpha_1
-1.000000e-10	0.806651	2	1.355493e+08	-1.355493e+08
-1.000000e-11	0.806651	2	1.355632e+09	-1.355632e+09
-9.999779e-13	0.806651	2	1.355997e+10	-1.355997e+10
-1.000311e-13	0.806651	2	1.357117e+11	-1.357117e+11
-9.992007e-15	0.806648	2	1.410632e+12	-1.410632e+12
-9.992007e-16	0.806616	2	1.008605e+00	1.008605e+00
-1.110223e-16	0.806616	1	1.008605e+00	1.008605e+00
0.000000e+00	0.806616	1	1.008605e+00	1.008605e+00

On fait un dernier test avec scikit-learn pour vérifier que l’algorithme de résolution donne des résultats similaires pour un cas où le déterminant est quasi-nul.

[26]:

from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score

alphas = [0.9 + i * 0.01 for i in range(11)]
res = []
for a in alphas:
    X = X_.copy()
    X[:, 1] = a * X[:, 0] + (1 - a) * X[:, 1]
    Y = X[:, 0] + X[:, 1] + X[:, 2]
    model = LinearRegression()
    model.fit(X[:, :2], Y)
    r2 = r2_score(Y, model.predict(X[:, :2]))
    res.append(dict(alpha=a, c1=model.coef_[0], c2=model.coef_[1], r2=r2))

import pandas

df = pandas.DataFrame(res)
df = df.set_index("alpha")
df

[26]:

	c1	c2	r2
alpha
0.90	1.140599	0.863675	0.791250
0.91	1.155746	0.848528	0.792821
0.92	1.174680	0.829593	0.794384
0.93	1.199024	0.805250	0.795940
0.94	1.231482	0.772791	0.797489
0.95	1.276924	0.727350	0.799029
0.96	1.345087	0.659187	0.800562
0.97	1.458691	0.545583	0.802087
0.98	1.685900	0.318374	0.803603
0.99	2.367526	-0.363252	0.805111
1.00	1.008682	1.008682	0.806575

[27]:

fig, ax = plt.subplots(1, 3, figsize=(12, 4))
df[["c1", "c2"]].plot(ax=ax[1])
df[["c1", "c2"]].plot(ax=ax[2])
df[["r2"]].plot(ax=ax[0])
ax[0].set_title("R2")
ax[1].set_title("coefficients")
ax[2].set_ylim([-5, 5])
ax[2].set_title("coefficients, échelle tronquée");

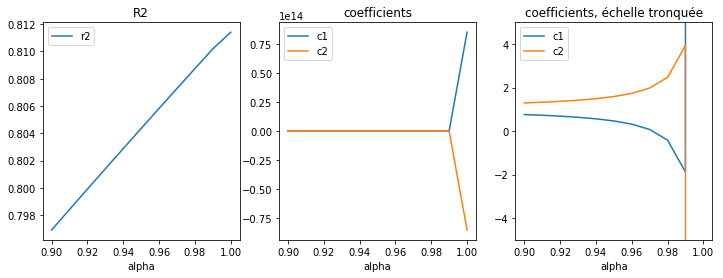
../../_images/notebooks_dsgarden_regression_lineaire_25_0.png

Le second graphe est trompeur mais il ne faut pas oublier de regarder l’échelle de l’axe des ordonnées.

Indicatrices¶

$X_1$ est une variable aléatoire gaussienne. On teste maintenant un modèle $Y = X'_1 + X'_2 + \epsilon$ avec $X'_1 = X_1 \mathbb{1}_{X_1 < 0}$ et $X'_2 = X_1 \mathbb{1}_{X_1 \geqslant 0}$ .

[28]:

X = npr.normal(size=(1000, 3))
X[:, 1] = X[:, 0]
X[X[:, 0] >= 0, 0] = 0
X[X[:, 1] < 0, 1] = 0
Y = X[:, 0] + X[:, 1] + X[:, 2]
corrcoef(X.T)

[28]:

array([[ 1.        ,  0.48561838,  0.0042644 ],
       [ 0.48561838,  1.        , -0.01058737],
       [ 0.0042644 , -0.01058737,  1.        ]])

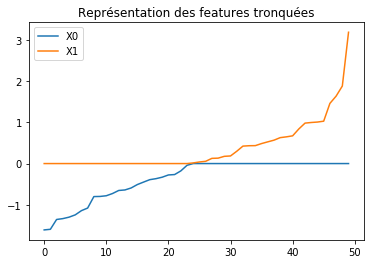
[29]:

from pandas import DataFrame

names = ["X%d" % i for i in range(X.shape[1] - 1)]
ax = (
    DataFrame(X[:50, :2], columns=names)
    .sort_values(names)
    .reset_index(drop=True)
    .plot()
)
ax.set_title("Représentation des features tronquées");

../../_images/notebooks_dsgarden_regression_lineaire_29_0.png

[30]:

model = OLS(Y, X[:, :3])
results = model.fit()
results.summary()

[30]:

OLS Regression Results
Dep. Variable:	y	R-squared (uncentered):	1.000
Model:	OLS	Adj. R-squared (uncentered):	1.000
Method:	Least Squares	F-statistic:	1.581e+33
Date:	Mon, 07 Oct 2024	Prob (F-statistic):	0.00
Time:	11:29:06	Log-Likelihood:	33532.
No. Observations:	1000	AIC:	-6.706e+04
Df Residuals:	997	BIC:	-6.704e+04
Df Model:	3
Covariance Type:	nonrobust

	coef	std err	t	P>\|t\|	[0.025	0.975]
x1	1.0000	2.98e-17	3.35e+16	0.000	1.000	1.000
x2	1.0000	2.73e-17	3.66e+16	0.000	1.000	1.000
x3	1.0000	2.09e-17	4.79e+16	0.000	1.000	1.000

Omnibus:	20.214	Durbin-Watson:	1.267
Prob(Omnibus):	0.000	Jarque-Bera (JB):	30.796
Skew:	0.179	Prob(JB):	2.05e-07
Kurtosis:	3.781	Cond. No.	1.43

Notes:
[1] R² is computed without centering (uncentered) since the model does not contain a constant.
[2] Standard Errors assume that the covariance matrix of the errors is correctly specified.

On découpe en trois.

[31]:

import numpy

X = npr.normal(size=(1000, 4))
for i in range(3):
    X[:, i] = X_[:, 0]
X[:, 3] = X_[:, 2]
X[X_[:, 0] > -1, 0] = 0
X[(X_[:, 0] < -1) | (X_[:, 0] > 1), 1] = 0
X[X_[:, 0] < 1, 2] = 0
Y = X[:, 0] + X[:, 1] + X[:, 2] + X[:, 3]
corrcoef(X.T)

[31]:

array([[ 1.        , -0.0221138 ,  0.15312241, -0.01158589],
       [-0.0221138 ,  1.        ,  0.02182757,  0.03734989],
       [ 0.15312241,  0.02182757,  1.        ,  0.01263351],
       [-0.01158589,  0.03734989,  0.01263351,  1.        ]])

[32]:

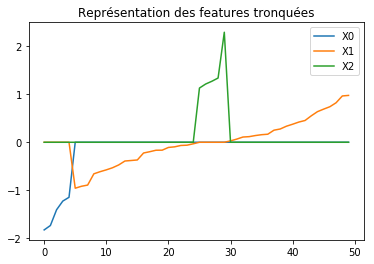
from pandas import DataFrame

names = ["X%d" % i for i in range(X.shape[1] - 1)]
ax = (
    DataFrame(X[:50, :3], columns=names)
    .sort_values(names)
    .reset_index(drop=True)
    .plot()
)
ax.set_title("Représentation des features tronquées");

../../_images/notebooks_dsgarden_regression_lineaire_33_0.png

[33]:

model = OLS(Y, X[:, :4])
results = model.fit()
results.summary()

[33]:

OLS Regression Results
Dep. Variable:	y	R-squared (uncentered):	1.000
Model:	OLS	Adj. R-squared (uncentered):	1.000
Method:	Least Squares	F-statistic:	3.030e+31
Date:	Mon, 07 Oct 2024	Prob (F-statistic):	0.00
Time:	11:29:06	Log-Likelihood:	31722.
No. Observations:	1000	AIC:	-6.344e+04
Df Residuals:	996	BIC:	-6.342e+04
Df Model:	4
Covariance Type:	nonrobust

	coef	std err	t	P>\|t\|	[0.025	0.975]
x1	1.0000	2.07e-16	4.84e+15	0.000	1.000	1.000
x2	1.0000	2.87e-16	3.49e+15	0.000	1.000	1.000
x3	1.0000	2.01e-16	4.97e+15	0.000	1.000	1.000
x4	1.0000	1.3e-16	7.66e+15	0.000	1.000	1.000

Omnibus:	457.510	Durbin-Watson:	1.879
Prob(Omnibus):	0.000	Jarque-Bera (JB):	1715.476
Skew:	2.280	Prob(JB):	0.00
Kurtosis:	7.514	Cond. No.	2.20

Notes:
[1] R² is computed without centering (uncentered) since the model does not contain a constant.
[2] Standard Errors assume that the covariance matrix of the errors is correctly specified.

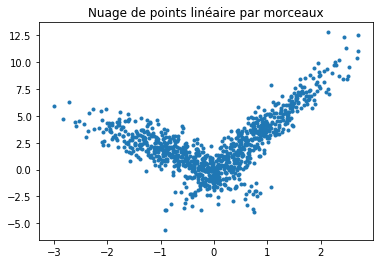
Régression linéaire par morceaux¶

On se place dans un cas particulier où le problème est linéaire par morceaux :

$Y = -2 X_1 \mathbb{1}_{X_1 + \epsilon_1 <0} + 4 X_1 \mathbb{1}_{X + \epsilon_1 > 0} + \epsilon_2$

La régression donne de très mauvais résultat sur ce type de problèmes mais on cherche une façon systématique de découper le problème en segments linéaires.

[34]:

X = npr.normal(size=(1000, 4))
alpha = [4, -2]
t = (X[:, 0] + X[:, 3] * 0.5) > 0
switch = numpy.zeros(X.shape[0])
switch[t] = 1
Y = alpha[0] * X[:, 0] * t + alpha[1] * X[:, 0] * (1 - t) + X[:, 2]

[35]:

fig, ax = plt.subplots(1, 1)
ax.plot(X[:, 0], Y, ".")
ax.set_title("Nuage de points linéaire par morceaux");

../../_images/notebooks_dsgarden_regression_lineaire_37_0.png

[36]:

model = OLS(Y, X[:, :1])
results = model.fit()
results.summary()

[36]:

OLS Regression Results
Dep. Variable:	y	R-squared (uncentered):	0.107
Model:	OLS	Adj. R-squared (uncentered):	0.106
Method:	Least Squares	F-statistic:	119.3
Date:	Mon, 07 Oct 2024	Prob (F-statistic):	2.56e-26
Time:	11:29:06	Log-Likelihood:	-2555.7
No. Observations:	1000	AIC:	5113.
Df Residuals:	999	BIC:	5118.
Df Model:	1
Covariance Type:	nonrobust

	coef	std err	t	P>\|t\|	[0.025	0.975]
x1	1.0940	0.100	10.924	0.000	0.897	1.290

Omnibus:	3.084	Durbin-Watson:	1.111
Prob(Omnibus):	0.214	Jarque-Bera (JB):	2.960
Skew:	0.088	Prob(JB):	0.228
Kurtosis:	2.801	Cond. No.	1.00

Notes:
[1] R² is computed without centering (uncentered) since the model does not contain a constant.
[2] Standard Errors assume that the covariance matrix of the errors is correctly specified.

[37]:

yp = results.predict(X[:, :1])

[38]:

fig, ax = plt.subplots(1, 1)
ax.plot(X[:, 0], Y, ".", label="expected")
ax.plot(X[:, 0], yp, ".", label="predicted")
ax.legend()
ax.set_title("Régression linéaire sur un nuage linéaire par morceaux");

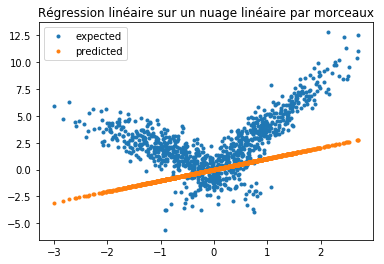
../../_images/notebooks_dsgarden_regression_lineaire_40_0.png

Passons à un arbre de décision qui n’est pas le meilleur modèle mais on va détourner ses résultats pour revenir à un problème de régression par morceaux.

[39]:

from sklearn.tree import DecisionTreeRegressor

model = DecisionTreeRegressor(min_samples_leaf=10, max_depth=3)
model.fit(X[:, :1], Y)
yp = model.predict(X[:, :1])

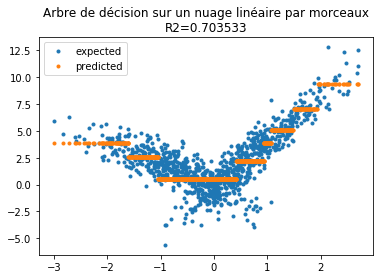
[40]:

fig, ax = plt.subplots(1, 1)
ax.plot(X[:, 0], Y, ".", label="expected")
ax.plot(X[:, 0], yp, ".", label="predicted")
ax.legend()
r2 = r2_score(Y, model.predict(X[:, :1]))
ax.set_title("Arbre de décision sur un nuage linéaire par morceaux\nR2=%f" % r2);

../../_images/notebooks_dsgarden_regression_lineaire_43_0.png

[41]:

import graphviz
from sklearn.tree import export_graphviz

dot = export_graphviz(model)

src = graphviz.Source(dot)
src.render("tree_dot.gv")

[41]:

'tree_dot.gv.pdf'

On extrait tous les seuils de l’arbre et on ajoute les milieux de segments.

[42]:

th = list(sorted(set(model.tree_.threshold)))
th += [(th[i] + th[i - 1]) / 2 for i in range(1, len(th))]
th = list(sorted(th))
th

[42]:

[np.float64(-2.0),
 np.float64(-1.85539710521698),
 np.float64(-1.71079421043396),
 np.float64(-1.3022041469812393),
 np.float64(-0.8936140835285187),
 np.float64(-0.2086283266544342),
 np.float64(0.47635743021965027),
 np.float64(0.6395495533943176),
 np.float64(0.802741676568985),
 np.float64(0.942541167140007),
 np.float64(1.082340657711029),
 np.float64(1.310522198677063),
 np.float64(1.538703739643097),
 np.float64(1.6980005204677582),
 np.float64(1.8572973012924194)]

On fait une régression sur les variables $W_{i>0} = X_1 \mathbb{1}_{X_1 > t_i}$ , $W_0 = X_1$ où les $(t_i)$ sont les seuils.

[43]:

W = numpy.zeros((X.shape[0], len(th) + 1))
x = X[:, 0]
W[:, 0] = x
for i in range(len(th)):
    W[x > th[i], i + 1] = x[x > th[i]]

[44]:

model = OLS(Y, W)
results = model.fit()
results.summary()

[44]:

OLS Regression Results
Dep. Variable:	y	R-squared (uncentered):	0.858
Model:	OLS	Adj. R-squared (uncentered):	0.855
Method:	Least Squares	F-statistic:	370.4
Date:	Mon, 07 Oct 2024	Prob (F-statistic):	0.00
Time:	11:29:07	Log-Likelihood:	-1637.5
No. Observations:	1000	AIC:	3307.
Df Residuals:	984	BIC:	3385.
Df Model:	16
Covariance Type:	nonrobust

	coef	std err	t	P>\|t\|	[0.025	0.975]
x1	-1.8183	0.119	-15.303	0.000	-2.051	-1.585
x2	-0.4155	0.260	-1.600	0.110	-0.925	0.094
x3	0.2157	0.320	0.673	0.501	-0.413	0.845
x4	0.1368	0.247	0.553	0.581	-0.349	0.622
x5	-0.2634	0.166	-1.589	0.112	-0.589	0.062
x6	1.0105	0.196	5.164	0.000	0.627	1.395
x7	3.3282	0.356	9.357	0.000	2.630	4.026
x8	1.3866	0.454	3.051	0.002	0.495	2.278
x9	0.3655	0.403	0.907	0.365	-0.425	1.156
x10	0.1177	0.334	0.353	0.724	-0.537	0.773
x11	-0.3147	0.307	-1.023	0.306	-0.918	0.289
x12	0.2972	0.255	1.166	0.244	-0.203	0.797
x13	-0.0456	0.197	-0.231	0.817	-0.433	0.342
x14	0.2807	0.252	1.112	0.266	-0.215	0.776
x15	-0.3102	0.303	-1.024	0.306	-0.904	0.284
x16	-0.0231	0.237	-0.097	0.923	-0.489	0.443

Omnibus:	207.506	Durbin-Watson:	1.993
Prob(Omnibus):	0.000	Jarque-Bera (JB):	673.510
Skew:	-0.999	Prob(JB):	5.61e-147
Kurtosis:	6.489	Cond. No.	37.1

Notes:
[1] R² is computed without centering (uncentered) since the model does not contain a constant.
[2] Standard Errors assume that the covariance matrix of the errors is correctly specified.

Dessinons les résultats de la prédictions.

[45]:

yp = results.predict(W)
fig, ax = plt.subplots(1, 1)
ax.plot(X[:, 0], Y, ".", label="expected")
ax.plot(X[:, 0], yp, ".", label="predicted")
ax.legend()
ax.set_title(
    "Régression linéaire par morceaux\nsur un nuage linéaire par morceaux\nR2=%f"
    % results.rsquared
);

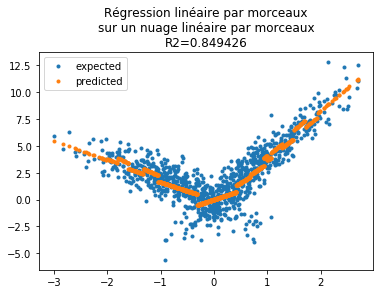
../../_images/notebooks_dsgarden_regression_lineaire_51_0.png

Le modèle nous suggère de ne garder que quelques seuils. En s’appuyant sur les p-values :

[46]:

keep = numpy.arange(len(results.pvalues))[results.pvalues < 0.05]
keep

[46]:

array([0, 5, 6, 7])

[47]:

W2 = W[:, keep]

[48]:

model = OLS(Y, W2)
results = model.fit()
results.summary()

[48]:

OLS Regression Results
Dep. Variable:	y	R-squared (uncentered):	0.856
Model:	OLS	Adj. R-squared (uncentered):	0.855
Method:	Least Squares	F-statistic:	1481.
Date:	Mon, 07 Oct 2024	Prob (F-statistic):	0.00
Time:	11:29:08	Log-Likelihood:	-1642.9
No. Observations:	1000	AIC:	3294.
Df Residuals:	996	BIC:	3314.
Df Model:	4
Covariance Type:	nonrobust

	coef	std err	t	P>\|t\|	[0.025	0.975]
x1	-1.9657	0.062	-31.604	0.000	-2.088	-1.844
x2	0.8316	0.163	5.106	0.000	0.512	1.151
x3	3.3282	0.355	9.363	0.000	2.631	4.026
x4	1.7842	0.327	5.455	0.000	1.142	2.426

Omnibus:	225.520	Durbin-Watson:	2.011
Prob(Omnibus):	0.000	Jarque-Bera (JB):	775.424
Skew:	-1.066	Prob(JB):	4.16e-169
Kurtosis:	6.750	Cond. No.	17.4

Notes:
[1] R² is computed without centering (uncentered) since the model does not contain a constant.
[2] Standard Errors assume that the covariance matrix of the errors is correctly specified.

[49]:

yp = results.predict(W2)
fig, ax = plt.subplots(1, 1)
ax.plot(X[:, 0], Y, ".", label="expected")
ax.plot(X[:, 0], yp, ".", label="predicted")
ax.legend()
ax.set_title(
    "Régression linéaire par morceaux\nsur un nuage linéaire par morceaux\n"
    + "réduction du nombre de segments\nR2=%f" % results.rsquared
);

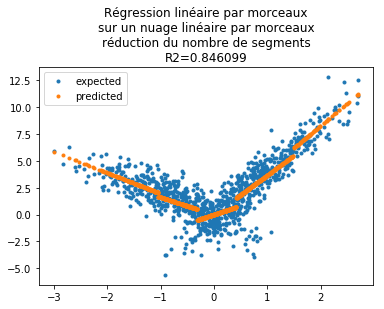
../../_images/notebooks_dsgarden_regression_lineaire_56_0.png

Le coefficient $R^2$ est quasiment identique pour un nombre de segments moindre. Je me suis amusé à rendre ce code plus générique pour comparer la première étape, le découpage en morceaux, via deux modèles, un arbre de décision et le nouvel objet KBinsDiscretizer qui segmente une variable sans tenir compte de la cible. La régression n’est plus nécessaire linéaire : Piecewise linear regression. Je me suis également amusé à faire de même pour une classification par morceaux PiecewiseClassifier. Celle-ci pose quelques soucis pratiques car toutes les classes ne sont pas forcément représentées dans chaque compartiment…

[41]:

Notebook on github