Corrélations non linéaires¶
Les corrélations indiquent si deux variables sont linéairement équivalentes. Comment étendre cette notion à des variables liées mais pas de façon linéaire.
[38]:
%matplotlib inline
Un exemple¶
[39]:
from sklearn import datasets
iris = datasets.load_iris()
X = iris.data
Y = iris.target
import pandas
df = pandas.DataFrame(X)
df.columns = ["X1", "X2", "X3", "X4"]
df.head()
[39]:
| X1 | X2 | X3 | X4 | |
|---|---|---|---|---|
| 0 | 5.1 | 3.5 | 1.4 | 0.2 |
| 1 | 4.9 | 3.0 | 1.4 | 0.2 |
| 2 | 4.7 | 3.2 | 1.3 | 0.2 |
| 3 | 4.6 | 3.1 | 1.5 | 0.2 |
| 4 | 5.0 | 3.6 | 1.4 | 0.2 |
[40]:
import seaborn as sns
sns.set()
sns.pairplot(df);
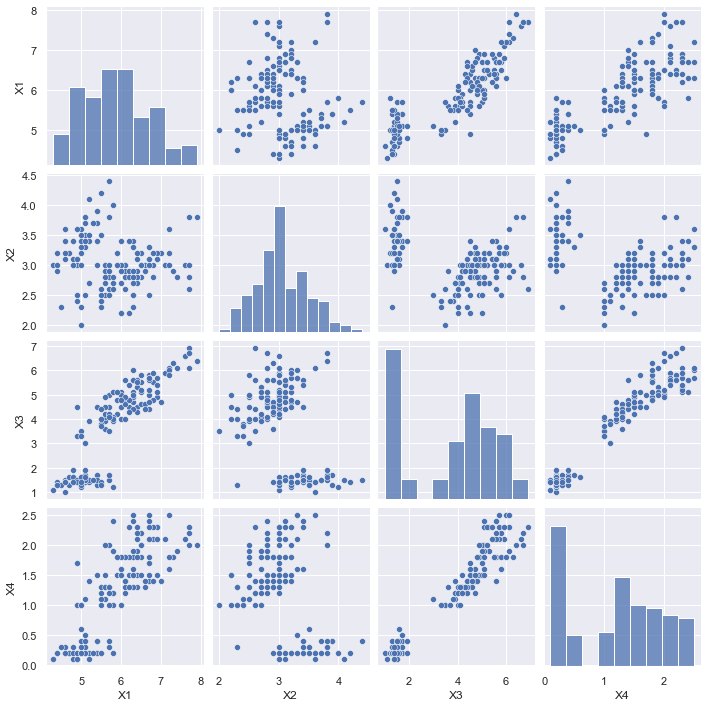
Et les corrélations :
[41]:
df.corr()
[41]:
| X1 | X2 | X3 | X4 | |
|---|---|---|---|---|
| X1 | 1.000000 | -0.117570 | 0.871754 | 0.817941 |
| X2 | -0.117570 | 1.000000 | -0.428440 | -0.366126 |
| X3 | 0.871754 | -0.428440 | 1.000000 | 0.962865 |
| X4 | 0.817941 | -0.366126 | 0.962865 | 1.000000 |
Un peu de théorie¶
Le coefficient de corrélation de Pearson est calculé comme suit :
Lorsque les variables sont centrées , cette formule devient :
Lorsque les variables sont réduites , cette formule devient
. Admettons maintenant que l’on cherche à trouver le coefficient
qui minimise la variance du bruit
:
Le coefficient est le résultat d’une régression linéaire qui minimise
. Si les variables
,
sont centrées et réduites :
. On étend cette définition dans le cas d’une fonction paramétrable
:
et d’une régression non linéaire. On suppose que les paramètres
minimisent la quantité
. On écrit alors
et on choisit
de telle sorte que
. On définit la corrélation non linéaire au sens de
:
On vérifie que ce coefficient est compris entre [0, 1]. Il est positif de manière évidente. Il est également inférieur à 1, si cela n’était pas le cas, nous pourrions construire une fonction qui est une meilleur solution pour le programme de minimisation. Ce nombre ressemble à une corrélation à ceci près qu’elle ne peut être négative.
Vérifications¶
Tout d’abord le cas linéaire :
[42]:
from sklearn.preprocessing import scale
import numpy
def correlation_etendue(df, model, **params):
cor = df.corr()
df = scale(df)
for i in range(cor.shape[0]):
xi = df[:, i : i + 1]
for j in range(cor.shape[1]):
mod = model(**params)
xj = df[:, j]
mod.fit(xi, xj)
v = mod.predict(xi)
c = numpy.std(v)
cor.iloc[i, j] = c
return cor
from sklearn.linear_model import LinearRegression
cor = correlation_etendue(df, LinearRegression, fit_intercept=False)
cor
[42]:
| X1 | X2 | X3 | X4 | |
|---|---|---|---|---|
| X1 | 1.000000 | 0.117570 | 0.871754 | 0.817941 |
| X2 | 0.117570 | 1.000000 | 0.428440 | 0.366126 |
| X3 | 0.871754 | 0.428440 | 1.000000 | 0.962865 |
| X4 | 0.817941 | 0.366126 | 0.962865 | 1.000000 |
On affiche à nouveau les corrélations qui sont identiques au signe près.
[43]:
df.corr()
[43]:
| X1 | X2 | X3 | X4 | |
|---|---|---|---|---|
| X1 | 1.000000 | -0.117570 | 0.871754 | 0.817941 |
| X2 | -0.117570 | 1.000000 | -0.428440 | -0.366126 |
| X3 | 0.871754 | -0.428440 | 1.000000 | 0.962865 |
| X4 | 0.817941 | -0.366126 | 0.962865 | 1.000000 |
Et le cas non linéaire :
[44]:
from sklearn.tree import DecisionTreeRegressor
cor = correlation_etendue(df, DecisionTreeRegressor)
cor
[44]:
| X1 | X2 | X3 | X4 | |
|---|---|---|---|---|
| X1 | 1.000000 | 0.544441 | 0.915847 | 0.879583 |
| X2 | 0.418274 | 1.000000 | 0.591839 | 0.539524 |
| X3 | 0.937056 | 0.789727 | 1.000000 | 0.978332 |
| X4 | 0.846161 | 0.761652 | 0.980005 | 1.000000 |
[45]:
from sklearn.ensemble import RandomForestRegressor
cor = correlation_etendue(df, RandomForestRegressor, n_estimators=10)
cor
[45]:
| X1 | X2 | X3 | X4 | |
|---|---|---|---|---|
| X1 | 0.997552 | 0.556704 | 0.920643 | 0.886171 |
| X2 | 0.426675 | 0.989691 | 0.574984 | 0.584174 |
| X3 | 0.943419 | 0.796293 | 0.999273 | 0.961729 |
| X4 | 0.848300 | 0.764006 | 0.973200 | 0.999983 |
Overfitting¶
Ces chiffres sont beaucoup trop optimistes. Les modèles de machine learning peuvent tout à fait faire de l’overfitting. Il faut améliorer la fonction en divisant en apprentissage et test plusieurs fois. Il faut également tenir compte de l’erreur de prédiction. On rappelle que :
Or et on suppose que les bruits ne sont pas corrélées linéairement aux
. On en déduit que
.
[46]:
from sklearn.model_selection import train_test_split
def correlation_cross_val(df, model, draws=5, **params):
cor = df.corr()
df = scale(df)
for i in range(cor.shape[0]):
xi = df[:, i : i + 1]
for j in range(cor.shape[1]):
xj = df[:, j]
mem = []
for k in range(draws):
xi_train, xi_test, xj_train, xj_test = train_test_split(
xi, xj, test_size=0.5
)
mod = model(**params)
mod.fit(xi_train, xj_train)
v = mod.predict(xi_test)
c = 1 - numpy.var(v - xj_test)
mem.append(max(c, 0) ** 0.5)
cor.iloc[i, j] = sum(mem) / len(mem)
return cor
cor = correlation_cross_val(df, LinearRegression, fit_intercept=False, draws=20)
cor
[46]:
| X1 | X2 | X3 | X4 | |
|---|---|---|---|---|
| X1 | 1.000000 | 0.153927 | 0.874786 | 0.814982 |
| X2 | 0.161970 | 1.000000 | 0.379941 | 0.323331 |
| X3 | 0.866726 | 0.445584 | 1.000000 | 0.964216 |
| X4 | 0.816849 | 0.405212 | 0.962288 | 1.000000 |
[47]:
cor = correlation_cross_val(df, DecisionTreeRegressor)
cor
[47]:
| X1 | X2 | X3 | X4 | |
|---|---|---|---|---|
| X1 | 0.998862 | 0.000000 | 0.857959 | 0.790670 |
| X2 | 0.089174 | 0.996104 | 0.317962 | 0.064916 |
| X3 | 0.865524 | 0.494974 | 0.999227 | 0.952608 |
| X4 | 0.716008 | 0.611972 | 0.962378 | 0.999387 |
[48]:
cor = correlation_cross_val(df, RandomForestRegressor, n_estimators=10)
cor
[48]:
| X1 | X2 | X3 | X4 | |
|---|---|---|---|---|
| X1 | 0.997563 | 0.036807 | 0.868202 | 0.809539 |
| X2 | 0.007906 | 0.996846 | 0.353607 | 0.150800 |
| X3 | 0.880475 | 0.547980 | 0.999167 | 0.956861 |
| X4 | 0.738863 | 0.591124 | 0.966500 | 0.999798 |
Les résultats sont assez fluctuants lorsque les données sont mal corrélées. On remarque également que la matrice n’est plus nécessairement symmétrique.
[ ]:
import matplotlib.pyplot as plt
def pairplot_cross_val(data, model=None, ax=None, **params):
if ax is None:
_fig, ax = plt.subplots(
data.shape[1], data.shape[1], figsize=params.get("figsize", (10, 10))
)
if "figsize" in params:
del params["figsize"]
if model is None:
from sklearn.linear_model import LinearRegression
model = LinearRegression
df = scale(data)
cor = numpy.corrcoef(df.T)
for i in range(cor.shape[0]):
xi = df[:, i : i + 1]
for j in range(cor.shape[1]):
xj = df[:, j]
xi_train, xi_test, xj_train, xj_test = train_test_split(
xi, xj, test_size=0.5
)
mod = model(**params)
mod.fit(xi_train, xj_train)
v = mod.predict(xi_test)
mod = model(**params)
mod.fit(xi_test, xj_test)
v2 = mod.predict(xi_train)
ax[i, j].plot(xj_test, v, ".")
ax[i, j].plot(xj_train, v2, ".")
if j == 0:
ax[i, j].set_ylabel(data.columns[i])
if i == data.shape[1] - 1:
ax[i, j].set_xlabel(data.columns[j])
mi = min(min(xj_test), min(v), min(xj_train), min(v2))
ma = max(max(xj_test), max(v), max(xj_train), max(v2))
ax[i, j].plot([mi, ma], [mi, ma], "--")
return ax
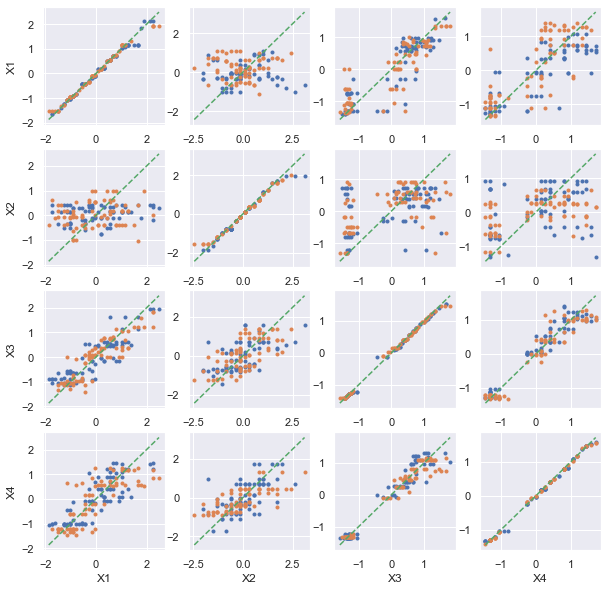
ax = pairplot_cross_val(df)
ax;
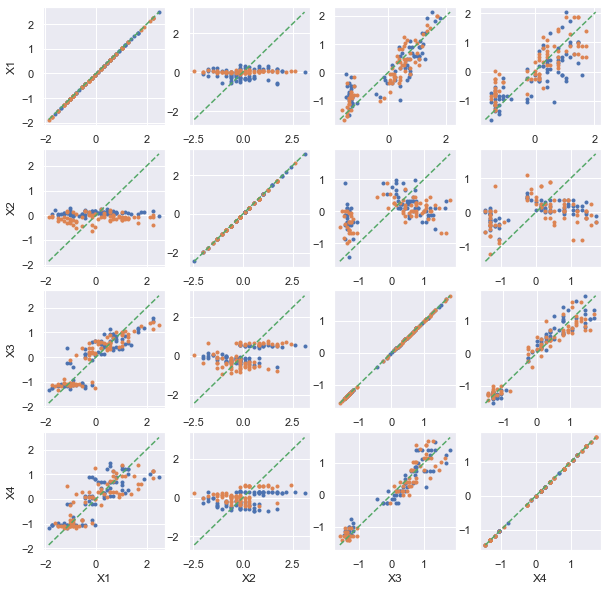
[50]:
ax = pairplot_cross_val(df, model=DecisionTreeRegressor)
ax;
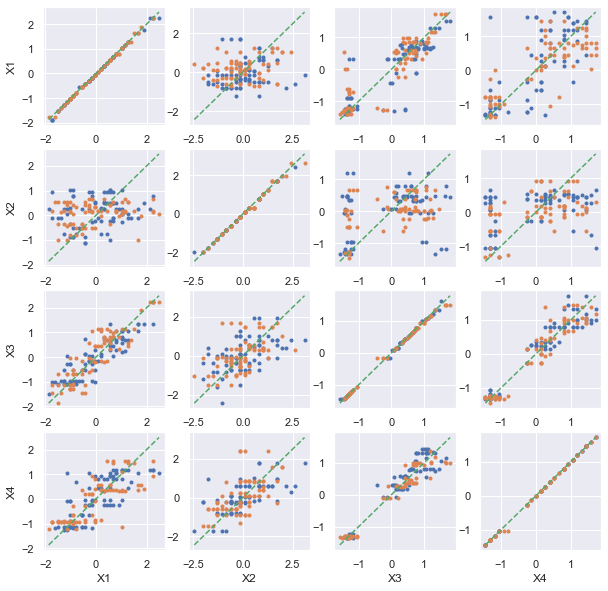
[51]:
ax = pairplot_cross_val(df, model=RandomForestRegressor, n_estimators=10)
ax;
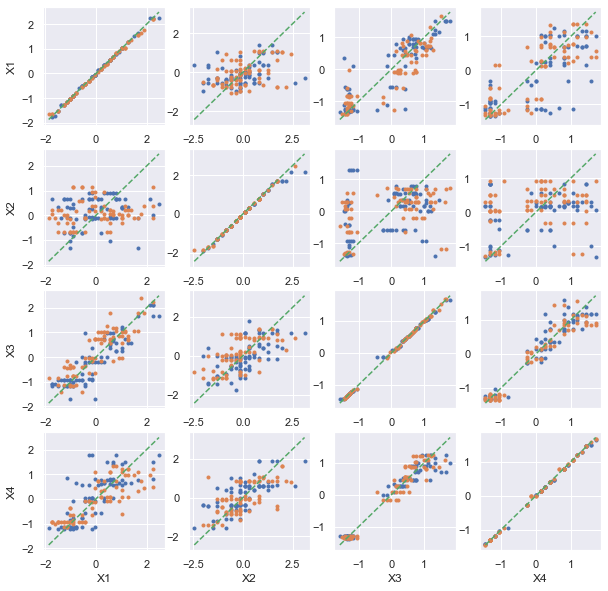
[52]:
from sklearn.neighbors import KNeighborsRegressor
ax = pairplot_cross_val(df, model=KNeighborsRegressor)
ax;
Corrélations de variables catégorielles¶
C’est le problème épineux si on se restreint au linéaire. Cela n’a pas trop de sens d’affecter une valeur à chaque catégorie et la corrélation de deux variables binaires (des modalités) est toujours étrange car il n’y a que deux valeurs possibles.
Dans le cas de variables binaires générées de modalités de la même variables catégorielles, le premier terme est toujours nul puisque les modalités sont exclusives et la corrélation est toujours négative.
[53]:
import random
ex = numpy.zeros((100, 2))
for i in range(ex.shape[0]):
h = random.randint(0, ex.shape[1] - 1)
ex[i, h] = 1
ex[:5]
[53]:
array([[0., 1.],
[0., 1.],
[0., 1.],
[1., 0.],
[0., 1.]])
[54]:
numpy.corrcoef(ex.T)
[54]:
array([[ 1., -1.],
[-1., 1.]])
[55]:
import random
ex = numpy.zeros((100, 3))
for i in range(ex.shape[0]):
h = random.randint(0, ex.shape[1] - 1)
ex[i, h] = 1
ex[:5]
numpy.corrcoef(ex.T)
[55]:
array([[ 1. , -0.59969254, -0.46164354],
[-0.59969254, 1. , -0.4330127 ],
[-0.46164354, -0.4330127 , 1. ]])
Supposons maintenant que nous avons deux variables catégorielles très proches :
est une couleur rouge, bleu, gris.
est une nuance rose, orange, cyan, magenta, blanc noir.
[56]:
c1 = ["rouge", "bleu", "gris"]
c2 = ["rose", "orange", "cyan", "magenta", "blanc", "noir"]
ind = [random.randint(0, 2) for i in range(100)]
x1 = [c1[i] for i in ind]
x2 = [c2[i * 2 + random.randint(0, 1)] for i in ind]
df = pandas.DataFrame(dict(X1=x1, X2=x2))
df.head()
[56]:
| X1 | X2 | |
|---|---|---|
| 0 | rouge | rose |
| 1 | gris | blanc |
| 2 | gris | blanc |
| 3 | gris | noir |
| 4 | bleu | magenta |
On peut évidemment transformer en entier.
[57]:
dummies = pandas.get_dummies(df)
dummies.head()
[57]:
| X1_bleu | X1_gris | X1_rouge | X2_blanc | X2_cyan | X2_magenta | X2_noir | X2_orange | X2_rose | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | False | False | True | False | False | False | False | False | True |
| 1 | False | True | False | True | False | False | False | False | False |
| 2 | False | True | False | True | False | False | False | False | False |
| 3 | False | True | False | False | False | False | True | False | False |
| 4 | True | False | False | False | False | True | False | False | False |
[58]:
dummies.corr()
[58]:
| X1_bleu | X1_gris | X1_rouge | X2_blanc | X2_cyan | X2_magenta | X2_noir | X2_orange | X2_rose | |
|---|---|---|---|---|---|---|---|---|---|
| X1_bleu | 1.000000 | -0.488085 | -0.394383 | -0.333096 | 0.524750 | 0.776643 | -0.254322 | -0.236067 | -0.263286 |
| X1_gris | -0.488085 | 1.000000 | -0.609560 | 0.682455 | -0.256123 | -0.379068 | 0.521061 | -0.364866 | -0.406936 |
| X1_rouge | -0.394383 | -0.609560 | 1.000000 | -0.415997 | -0.206952 | -0.306295 | -0.317618 | 0.598572 | 0.667590 |
| X2_blanc | -0.333096 | 0.682455 | -0.415997 | 1.000000 | -0.174792 | -0.258697 | -0.268260 | -0.249004 | -0.277716 |
| X2_cyan | 0.524750 | -0.256123 | -0.206952 | -0.174792 | 1.000000 | -0.128698 | -0.133456 | -0.123876 | -0.138159 |
| X2_magenta | 0.776643 | -0.379068 | -0.306295 | -0.258697 | -0.128698 | 1.000000 | -0.197518 | -0.183340 | -0.204479 |
| X2_noir | -0.254322 | 0.521061 | -0.317618 | -0.268260 | -0.133456 | -0.197518 | 1.000000 | -0.190117 | -0.212039 |
| X2_orange | -0.236067 | -0.364866 | 0.598572 | -0.249004 | -0.123876 | -0.183340 | -0.190117 | 1.000000 | -0.196818 |
| X2_rose | -0.263286 | -0.406936 | 0.667590 | -0.277716 | -0.138159 | -0.204479 | -0.212039 | -0.196818 | 1.000000 |
Ca ne dit pas grand-chose.
[59]:
from sklearn.preprocessing import LabelEncoder
enc = LabelEncoder()
df["X1e"] = enc.fit_transform(df["X1"])
df["X2e"] = enc.fit_transform(df["X2"])
df.head()
[59]:
| X1 | X2 | X1e | X2e | |
|---|---|---|---|---|
| 0 | rouge | rose | 2 | 5 |
| 1 | gris | blanc | 1 | 0 |
| 2 | gris | blanc | 1 | 0 |
| 3 | gris | noir | 1 | 3 |
| 4 | bleu | magenta | 0 | 2 |
[60]:
df.select_dtypes(exclude=["object"]).corr()
[60]:
| X1e | X2e | |
|---|---|---|
| X1e | 1.000000 | 0.644442 |
| X2e | 0.644442 | 1.000000 |
Ca ne veut toujours pas dire grand-chose. Et si on change la première colonne en permutant les lables :
[61]:
df["X1e"] = df["X1e"].apply(lambda i: (i + 1) % 3)
df.head()
[61]:
| X1 | X2 | X1e | X2e | |
|---|---|---|---|---|
| 0 | rouge | rose | 0 | 5 |
| 1 | gris | blanc | 2 | 0 |
| 2 | gris | blanc | 2 | 0 |
| 3 | gris | noir | 2 | 3 |
| 4 | bleu | magenta | 1 | 2 |
[62]:
df.select_dtypes(exclude=["object"]).corr()
[62]:
| X1e | X2e | |
|---|---|---|
| X1e | 1.000000 | -0.777554 |
| X2e | -0.777554 | 1.000000 |
La corrélation linéaire sur des variables catégorielles n’a pas de sens. Essayons avec un arbre de décision. C’est le modèle adéquat pour ce type de valeur discrètes :
[63]:
cor = correlation_cross_val(df[["X1e", "X2e"]], DecisionTreeRegressor)
cor
[63]:
| X1e | X2e | |
|---|---|---|
| X1e | 1.0 | 0.786412 |
| X2e | 1.0 | 1.000000 |
Et si on permute le premier label :
[64]:
df["X1e"] = df["X1e"].apply(lambda i: (i + 1) % 3)
correlation_cross_val(df[["X1e", "X2e"]], DecisionTreeRegressor)
[64]:
| X1e | X2e | |
|---|---|---|
| X1e | 1.0 | 0.828978 |
| X2e | 1.0 | 1.000000 |
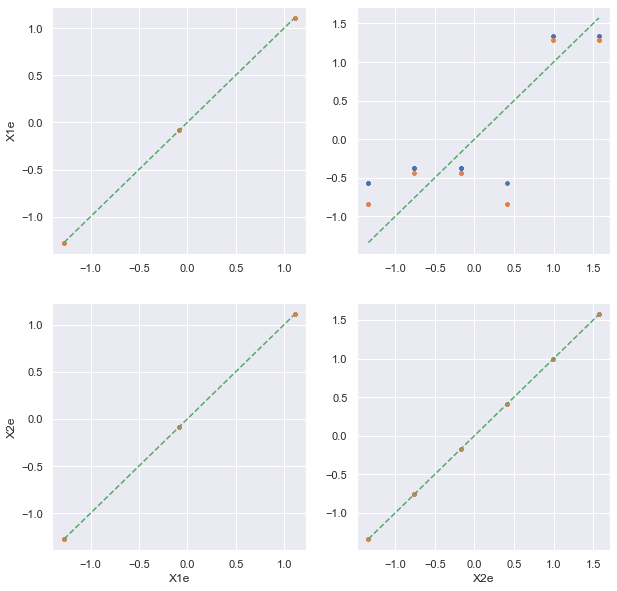
Même résultat qui s’interprète de la sorte :
La variable X1e se déduit de X2e (car cor(X2e, X1e) = 1).
La variable X2e et fortement lié à X2e.
La valeur numérique choisie pour représente la variable catégorielle n’a pas d’impact sur les résultats.
[65]:
ax = pairplot_cross_val(df[["X1e", "X2e"]], model=DecisionTreeRegressor)
ax;
Et sur un jeu de données plus complet.
[66]:
from sklearn.datasets import load_diabetes
df = load_diabetes()
df = pandas.DataFrame(df.data, columns=df.feature_names)
df.head()
[66]:
| age | sex | bmi | bp | s1 | s2 | s3 | s4 | s5 | s6 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.038076 | 0.050680 | 0.061696 | 0.021872 | -0.044223 | -0.034821 | -0.043401 | -0.002592 | 0.019907 | -0.017646 |
| 1 | -0.001882 | -0.044642 | -0.051474 | -0.026328 | -0.008449 | -0.019163 | 0.074412 | -0.039493 | -0.068332 | -0.092204 |
| 2 | 0.085299 | 0.050680 | 0.044451 | -0.005670 | -0.045599 | -0.034194 | -0.032356 | -0.002592 | 0.002861 | -0.025930 |
| 3 | -0.089063 | -0.044642 | -0.011595 | -0.036656 | 0.012191 | 0.024991 | -0.036038 | 0.034309 | 0.022688 | -0.009362 |
| 4 | 0.005383 | -0.044642 | -0.036385 | 0.021872 | 0.003935 | 0.015596 | 0.008142 | -0.002592 | -0.031988 | -0.046641 |
[67]:
df.corr()
[67]:
| age | sex | bmi | bp | s1 | s2 | s3 | s4 | s5 | s6 | |
|---|---|---|---|---|---|---|---|---|---|---|
| age | 1.000000 | 0.173737 | 0.185085 | 0.335428 | 0.260061 | 0.219243 | -0.075181 | 0.203841 | 0.270774 | 0.301731 |
| sex | 0.173737 | 1.000000 | 0.088161 | 0.241010 | 0.035277 | 0.142637 | -0.379090 | 0.332115 | 0.149916 | 0.208133 |
| bmi | 0.185085 | 0.088161 | 1.000000 | 0.395411 | 0.249777 | 0.261170 | -0.366811 | 0.413807 | 0.446157 | 0.388680 |
| bp | 0.335428 | 0.241010 | 0.395411 | 1.000000 | 0.242464 | 0.185548 | -0.178762 | 0.257650 | 0.393480 | 0.390430 |
| s1 | 0.260061 | 0.035277 | 0.249777 | 0.242464 | 1.000000 | 0.896663 | 0.051519 | 0.542207 | 0.515503 | 0.325717 |
| s2 | 0.219243 | 0.142637 | 0.261170 | 0.185548 | 0.896663 | 1.000000 | -0.196455 | 0.659817 | 0.318357 | 0.290600 |
| s3 | -0.075181 | -0.379090 | -0.366811 | -0.178762 | 0.051519 | -0.196455 | 1.000000 | -0.738493 | -0.398577 | -0.273697 |
| s4 | 0.203841 | 0.332115 | 0.413807 | 0.257650 | 0.542207 | 0.659817 | -0.738493 | 1.000000 | 0.617859 | 0.417212 |
| s5 | 0.270774 | 0.149916 | 0.446157 | 0.393480 | 0.515503 | 0.318357 | -0.398577 | 0.617859 | 1.000000 | 0.464669 |
| s6 | 0.301731 | 0.208133 | 0.388680 | 0.390430 | 0.325717 | 0.290600 | -0.273697 | 0.417212 | 0.464669 | 1.000000 |
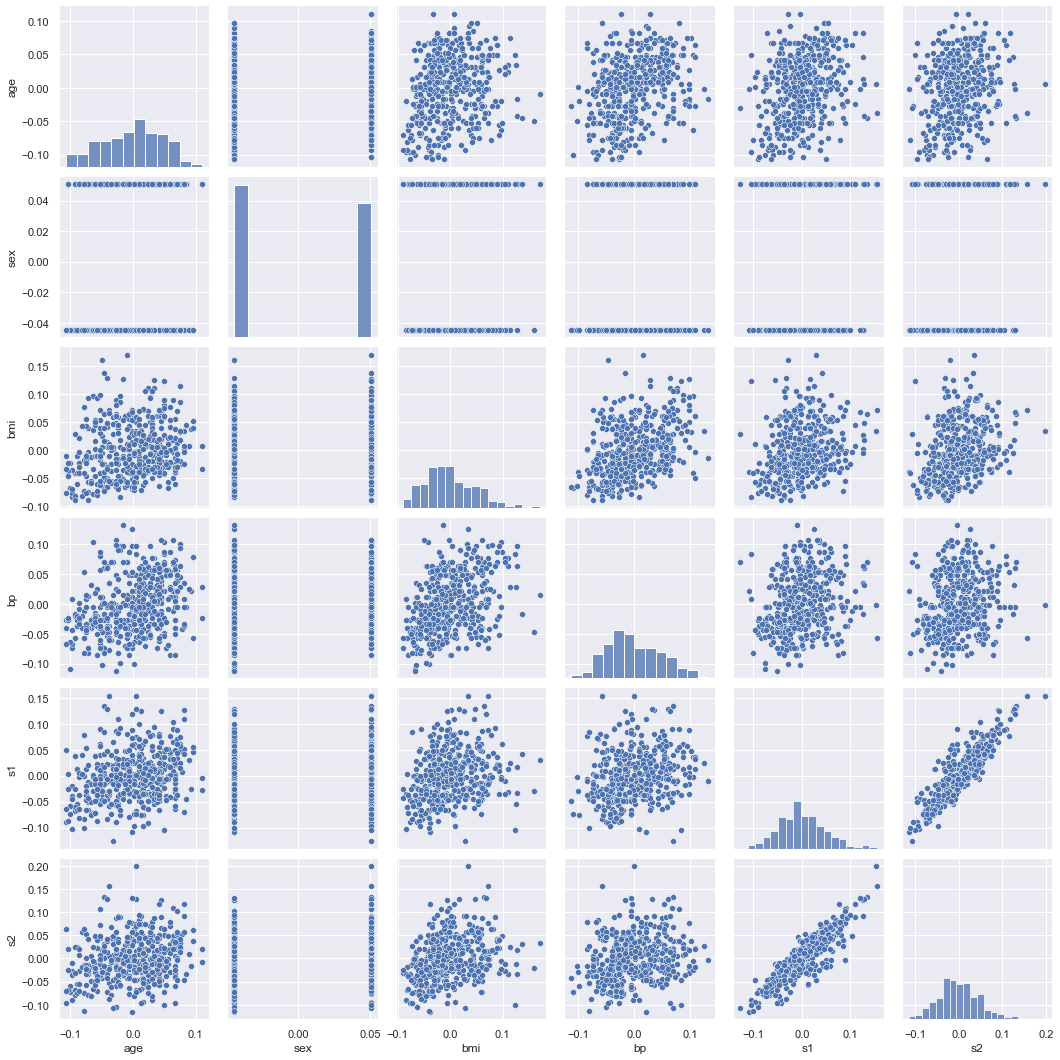
On dessine les 5 premières variables. On voit que la variable CHAS est binaire.
[68]:
sns.pairplot(df[df.columns[:6]]);
[69]:
correlation_cross_val(df, DecisionTreeRegressor)
[69]:
| age | sex | bmi | bp | s1 | s2 | s3 | s4 | s5 | s6 | |
|---|---|---|---|---|---|---|---|---|---|---|
| age | 0.999796 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| sex | 0.164976 | 1.000000 | 0.164644 | 0.250477 | 0.045777 | 0.111387 | 0.369474 | 0.252741 | 0.182065 | 0.180895 |
| bmi | 0.000000 | 0.000000 | 0.998916 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| bp | 0.000000 | 0.000000 | 0.000000 | 0.999504 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.032632 | 0.000000 |
| s1 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.999636 | 0.812438 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| s2 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.768708 | 0.997999 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| s3 | 0.000000 | 0.079495 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.999542 | 0.719799 | 0.157711 | 0.000000 |
| s4 | 0.053803 | 0.104578 | 0.285713 | 0.000000 | 0.375567 | 0.613688 | 0.728683 | 0.998655 | 0.554312 | 0.285438 |
| s5 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.127121 | 0.999332 | 0.000000 |
| s6 | 0.000000 | 0.000000 | 0.000000 | 0.053945 | 0.013372 | 0.000000 | 0.000000 | 0.000000 | 0.047138 | 0.999331 |
[70]:
pairplot_cross_val(df[df.columns[:6]], model=DecisionTreeRegressor, figsize=(16, 16));
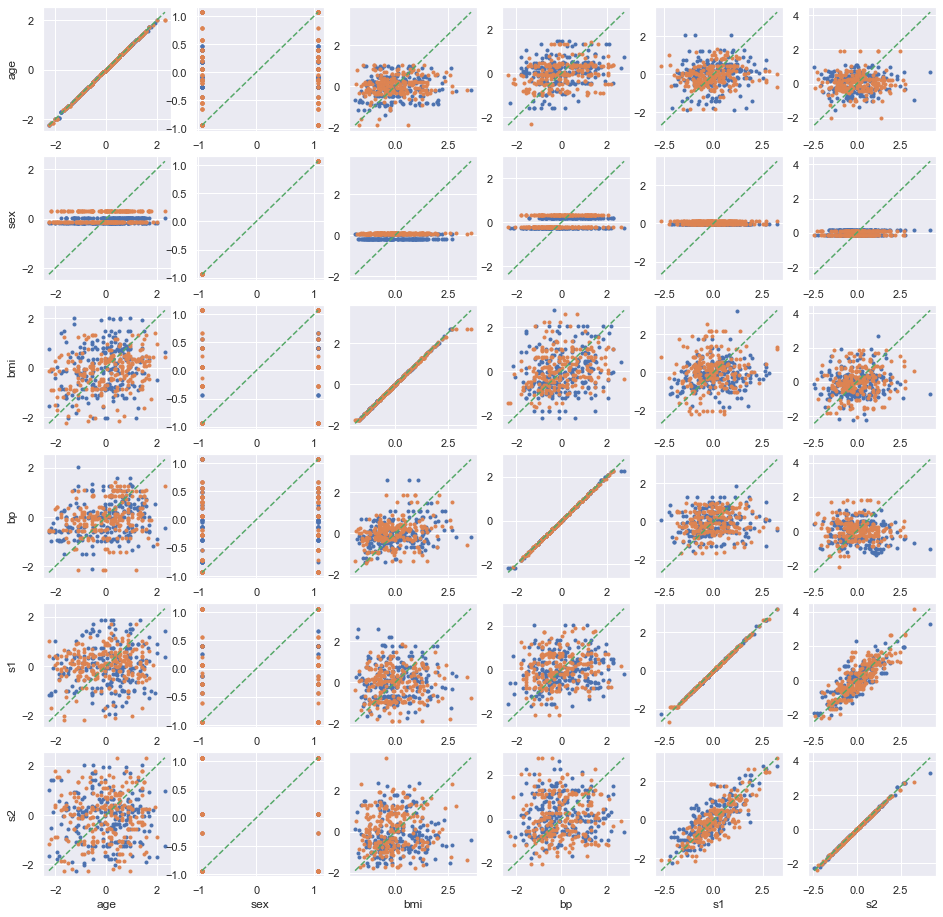
On regarde en pariculier les variables TAX, RAD, PTRATIO.
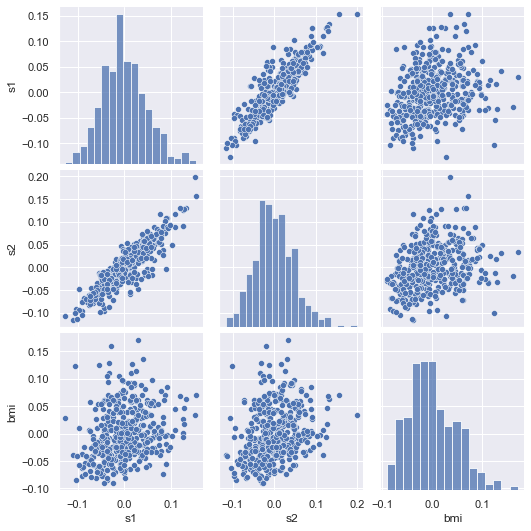
[71]:
sns.pairplot(df[["s1", "s2", "bmi"]]);
[72]:
df[["s1", "s2", "bmi"]].corr()
[72]:
| s1 | s2 | bmi | |
|---|---|---|---|
| s1 | 1.000000 | 0.896663 | 0.249777 |
| s2 | 0.896663 | 1.000000 | 0.261170 |
| bmi | 0.249777 | 0.261170 | 1.000000 |
[73]:
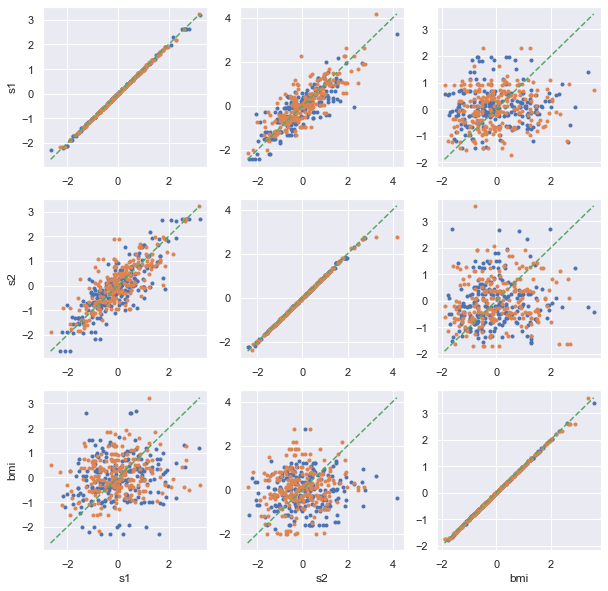
pairplot_cross_val(df[["s1", "s2", "bmi"]], model=DecisionTreeRegressor);
[74]:
correlation_cross_val(df[["s1", "s2", "bmi"]], DecisionTreeRegressor)
[74]:
| s1 | s2 | bmi | |
|---|---|---|---|
| s1 | 0.999550 | 0.809505 | 0.00000 |
| s2 | 0.783178 | 0.997555 | 0.00000 |
| bmi | 0.000000 | 0.000000 | 0.99898 |
Les variables sont toutes trois liées de façon non linéaire.
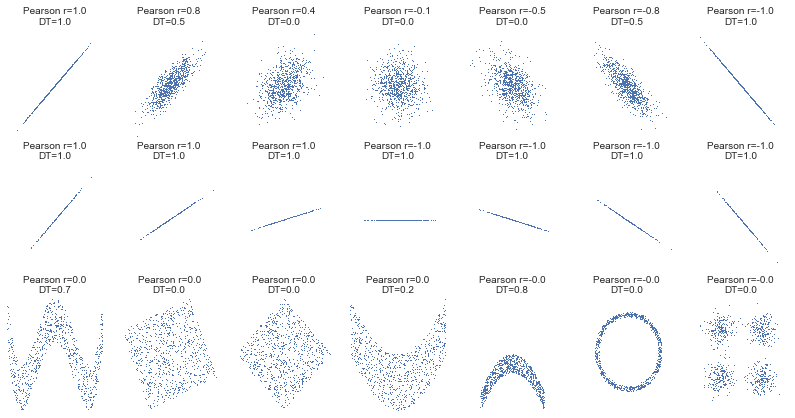
Maximal information coefficient¶
Cette approche est plutôt pragmatique mais peut se révéler coûteuse en terme de calculs. Elle permet aussi de comprendre qu’un coefficient de corrélation dépend des hypothèses qu’on choisi pour les données. On peut toujours construire un coefficient de corrélation qui soit égal à 1 mais il correspond à toujours à un phénomène qu’on souhaite étudier. La corrélation linéaire recherche des relations linéaires. On peut chercher une relation polynomiale. Les arbres de décision recherche une corrélation construite à partir de fonction en escalier. Plus la relation a de degré de liberté, plus le coefficient a de chance de tendre vers 1, moins il a de chance d’être aussi élevé sur de nouvelles données.
Cela permet néanmoins de mieux comprendre les avantages et les inconvénients de métriques du type MIC ou Maximal information coefficient. Plus de détails sont disponibles dans cet article : Equitability, mutual information, and the maximal information coefficient. Le module minepy implémente cette métrique ainsi que d’autres qui poursuivent le même objectif. L’information mutuelle est définie comme ceci pour deux variables discrètes :
La fonction définit la distribution conjointe des deux variables,
,
les deux probabilités marginales. Il existe une extension pour les variables continues :
Une façon de calculer une approximation du coefficient est de discrétiser les deux variables
et
ce qu’on fait en appliquant un algorithme similaire à celui utilisé pour construire un arbre de décision à ceci près que qu’il n’y a qu’une seule variable et que la variable à prédire est elle-même.
L’information mutuelle est inspiré de la distance de Kullback-Leiber qui est une distance entre deux probabilités qui sont ici la disribution du couple et la distribution que ce couple aurait si les deux variables étaient indépendantes, c’est à dire le produit de leur distribution.
[75]:
%matplotlib inline
[76]:
import numpy as np
rs = np.random.RandomState(seed=0)
def mysubplot(x, y, numRows, numCols, plotNum, xlim=(-4, 4), ylim=(-4, 4)):
r = np.around(np.corrcoef(x, y)[0, 1], 1)
# début ajout
df = pandas.DataFrame(dict(x=x, y=y))
cor = correlation_cross_val(df, DecisionTreeRegressor)
dt = max(cor.iloc[1, 0], cor.iloc[0, 1])
ax = plt.subplot(numRows, numCols, plotNum, xlim=xlim, ylim=ylim)
ax.set_title("Pearson r=%.1f\nDT=%.1f" % (r, dt), fontsize=10)
ax.set_frame_on(False)
ax.axes.get_xaxis().set_visible(False)
ax.axes.get_yaxis().set_visible(False)
ax.plot(x, y, ",")
ax.set_xticks([])
ax.set_yticks([])
return ax
def rotation(xy, t):
return np.dot(xy, [[np.cos(t), -np.sin(t)], [np.sin(t), np.cos(t)]])
def mvnormal(n=1000):
cors = [1.0, 0.8, 0.4, 0.0, -0.4, -0.8, -1.0]
for i, cor in enumerate(cors):
cov = [[1, cor], [cor, 1]]
xy = rs.multivariate_normal([0, 0], cov, n)
mysubplot(xy[:, 0], xy[:, 1], 3, 7, i + 1)
def rotnormal(n=1000):
ts = [
0,
np.pi / 12,
np.pi / 6,
np.pi / 4,
np.pi / 2 - np.pi / 6,
np.pi / 2 - np.pi / 12,
np.pi / 2,
]
cov = [[1, 1], [1, 1]]
xy = rs.multivariate_normal([0, 0], cov, n)
for i, t in enumerate(ts):
xy_r = rotation(xy, t)
mysubplot(xy_r[:, 0], xy_r[:, 1], 3, 7, i + 8)
def others(n=1000):
x = rs.uniform(-1, 1, n)
y = 4 * (x**2 - 0.5) ** 2 + rs.uniform(-1, 1, n) / 3
mysubplot(x, y, 3, 7, 15, (-1, 1), (-1 / 3, 1 + 1 / 3))
y = rs.uniform(-1, 1, n)
xy = np.concatenate((x.reshape(-1, 1), y.reshape(-1, 1)), axis=1)
xy = rotation(xy, -np.pi / 8)
lim = np.sqrt(2 + np.sqrt(2)) / np.sqrt(2)
mysubplot(xy[:, 0], xy[:, 1], 3, 7, 16, (-lim, lim), (-lim, lim))
xy = rotation(xy, -np.pi / 8)
lim = np.sqrt(2)
mysubplot(xy[:, 0], xy[:, 1], 3, 7, 17, (-lim, lim), (-lim, lim))
y = 2 * x**2 + rs.uniform(-1, 1, n)
mysubplot(x, y, 3, 7, 18, (-1, 1), (-1, 3))
y = (x**2 + rs.uniform(0, 0.5, n)) * np.array([-1, 1])[rs.randint(0, 1, size=n)]
mysubplot(x, y, 3, 7, 19, (-1.5, 1.5), (-1.5, 1.5))
y = np.cos(x * np.pi) + rs.uniform(0, 1 / 8, n)
x = np.sin(x * np.pi) + rs.uniform(0, 1 / 8, n)
mysubplot(x, y, 3, 7, 20, (-1.5, 1.5), (-1.5, 1.5))
xy1 = np.random.multivariate_normal([3, 3], [[1, 0], [0, 1]], int(n / 4))
xy2 = np.random.multivariate_normal([-3, 3], [[1, 0], [0, 1]], int(n / 4))
xy3 = np.random.multivariate_normal([-3, -3], [[1, 0], [0, 1]], int(n / 4))
xy4 = np.random.multivariate_normal([3, -3], [[1, 0], [0, 1]], int(n / 4))
xy = np.concatenate((xy1, xy2, xy3, xy4), axis=0)
mysubplot(xy[:, 0], xy[:, 1], 3, 7, 21, (-7, 7), (-7, 7))
plt.figure(figsize=(14, 7))
mvnormal(n=800)
rotnormal(n=200)
others(n=800)
# plt.tight_layout()
# plt.show()
[41]: