Mélange de lois normales¶

Algorithme EM¶

Définition D1 : mélange de lois normales

Soit $X$ une variable aléatoire d’un espace vectoriel de dimension $d$ , $X$ suit un la loi d’un mélange de $N$ lois gaussiennes de paramètres $\pa{\mu_i, \Sigma_i}_ {1 \leqslant i \leqslant N}$ , alors la densité $f$ de $X$ est de la forme :

$\begin{eqnarray} f\pa{x} &=& \sum_{i=1}^{N} \; p_i \; \dfrac{1}{\pa{2 \pi}^{\frac{d}{2}}\sqrt{\det \Sigma_i}} \; exp \pa{-\frac{1}{2} \pa{x-\mu_i}' \Sigma_i^{-1} \pa{x-\mu_i} } \\ \end{eqnarray}$

Avec : $\sum_{i=1}^{N} \; p_i = 1$ .

Dans le cas d’une loi normale à valeur réelle $\Sigma = \sigma^2$ , l’algorithme permet d’estimer la loi de l’échantillon $\vecteur{X_1}{X_T}$ , il s’effectue en plusieurs itérations, les paramètres $p_i\pa{0}$ , $\mu_i\pa{0}$ , $\sigma^2\pa{0}$ sont choisis de manière aléatoire, à l’itération $t+1$ , la mise à jour des coefficients est faite comme suit :

$\begin{eqnarray} f_{k,i}\pa{t} &=& p_i \pa{t} \; \dfrac{1}{\pa{2 \pi}^{\frac{d}{2}}\sqrt{\det \Sigma_i\pa{t}}} \; \exp \pa{-\frac{1}{2} \pa{X_k-\mu_i\pa{t}}' \Sigma_i^{-1}\pa{t} \pa{X_k-\mu_i\pa{t}} } \\ \overline{f_{k,i}}\pa{t} &=& \frac{ f_{k,i}\pa{t} } { \sum_{i} \, f_{k,i}\pa{t} } \\ p_i\pa{t+1} &=& \frac{1}{T} \; \sum_{k=1}^{T} \; \overline{f_{k,i}}\pa{t} \\ \mu_i\pa{t+1} &=& \cro{ \sum_{k=1}^{T} \; \overline{f_{k,i}}\pa{t} }^{-1} \; \sum_{k=1}^{T} \overline{f_{k,i}}\pa{t} X_k \\ \Sigma^2_i\pa{t+1} &=& \cro{ \sum_{k=1}^{T} \; \overline{f_{k,i}}\pa{t} }^{-1} \; \sum_{k=1}^{T} \overline{f_{k,i}}\pa{t} \, \pa{ X_k - \mu_i\pa{t+1}} \pa{ X_k - \mu_i\pa{t+1}}' \end{eqnarray}$

L’estimation d’une telle densité s’effectue par l’intermédiaire d’un algorithme de type Expectation Maximization (EM) (voir [Dempster1977]) ou de ses variantes SEM, SAEM, … (voir [Celeux1985], [Celeux1985b]). La sélection du nombre de lois dans le mélange reste un problème ouvert abordé par l’article [Biernacki2001].

Competitive EM algorithm¶

L’algorithme développé dans l’article [ZhangB2004] tente de corriger les défauts de l’algorithme EM. Cette nouvelle version appelée « Competitive EM » ou CEM s’applique à un mélange de lois - normales en particulier -, il détermine le nombre de classes optimal en supprimant ou en ajoutant des classes.

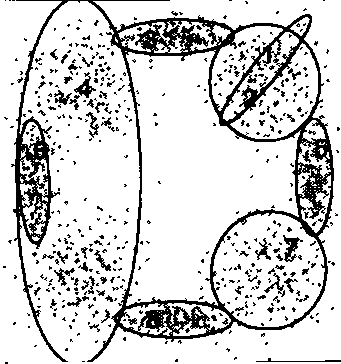
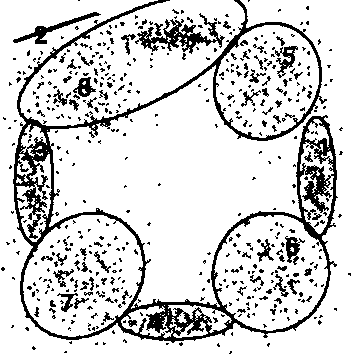
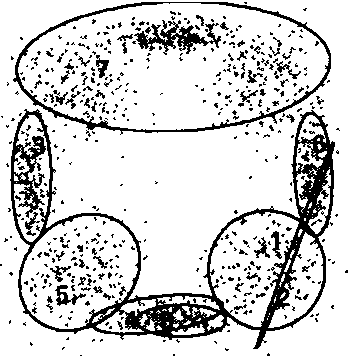
Figures extraites de [ZhangB2004], la première image montre deux classes incluant deux autres classes qui devrait donc être supprimées. La seconde image montre une classe aberrante tandis que la troisième image montre des classes se recouvrant partiellement.

On considère un échantillon de variables aléatoires indépendantes et identiquement distribuées à valeur dans un espace vectoriel de dimension $d$ . Soit $X$ une telle variable, on suppose que $X$ suit la loi du mélange suivant :

$f\pa{X \sac \theta} = \sum_{i=1}^{k} \alpha_i \, f\pa{X \sac \theta_i}$

Avec : $\theta = \pa{\alpha_i,\theta_i}_{1 \leqslant i \leqslant k}, \; \forall i, \; \alpha_i \supegal 0$ et $\sum_{i=1}^{k} \alpha_i = 1$ .

On définit pour une classe $m$ la probabilité $P_{split}(m, \theta)$ qu’elle doive être divisée et celle qu’elle doive être associée à une autre $P_{merge}(m,l, \theta)$ . Celles ci sont définies comme suit :

(1)¶ $\begin{eqnarray} P_{split}(m, \theta) &=& \frac{J\pa{m,\theta}}{Z\pa{\theta}} \\ P_{merge}(m,l, \theta) &=& \frac{\beta}{J\pa{m,\theta}Z\pa{\theta}} \end{eqnarray}$

$\beta$ est une constante définie par expériences. $J\pa{m,\theta}$ est défini pour l’échantillon $\vecteur{x_1}{x_n}$ par :

$J\pa{m,\theta} = \int f_m\pa{x,\theta} \; \log \frac{f_m\pa{x,\theta}}{p_m\pa{x,\theta_m}} \, dx$

Où : $f_m\pa{x,\theta} = \frac{ \sum_{i=1}^{n} \, \indicatrice{x = x_i} \, \pr{ m \sac x_i,\theta} } { \sum_{i=1}^{n} \, \pr{ m \sac x_i,\theta}}$ .

La constante $Z\pa{\theta}$ est choisie de telle sorte que les probabilités $P_{split}(m, \theta)$ et $P_{merge}(m,l, \theta)$ vérifient :

$\sum_{m=1}^{k} \, P_{split}(m, \theta) + \sum_{m=1}^{k} \, \sum_{l=m+1}^{k} \, P_{merge}(m,l, \theta) = 1$

L’algorithme EM permet de construire une suite $\hat{\theta_t}$ maximisant la vraisemblance à partir de poids $\hat{\theta_0}$ . L’algorithme CEM est dérivé de l’algorithme EM :

Algorithme A1 : CEM

Les notations sont celles utilisées dans les paragraphes précédents. On suppose que la variable aléatoire $Z=\pa{X,Y}$ où $X$ est la variable observée et $Y$ la variable cachée. $T$ désigne le nombre maximal d’itérations.

initialisation

Choix arbitraire de $k$ et $\hat{\theta}_0$ .

Expectation

$Q\pa{\theta,\hat{\theta}_t } = \esp{ \pa{\log \cro{ f\pa{ X,Y \sac \theta }} \sac X, \hat{\theta}_t }}$

Maximization

$\hat{\theta}_{t+1} = \underset{\theta}{\arg \max} \; Q\pa{\theta,\hat{\theta}_t }$

convergence

$t \longleftarrow t + 1$ , si $\hat{\theta}_t$ n’a pas convergé vers un maximum local, alors on retourne à l’étape Expectation.

division ou regroupement

Dans le cas contraire, on estime les probabilités $P_{split}(m, \theta)$ et $P_{merge}(m,l, \theta)$ définie par les expressions (1). On choisit aléatoirement une division ou un regroupement (les choix les plus probables ayant le plus de chance d’être sélectionnés). Ceci mène au paramètre $\theta'_t$ dont la partie modifiée par rapport à $\hat{\theta}_t$ est déterminée de manière aléatoire. L’algorithme EM est alors appliqué aux paramètres $\theta'_t$ jusqu’à convergence aux paramètres $\theta''_t$ .

acceptation

On calcule le facteur suivant :

$P_a = \min \acc{ \exp\cro{ \frac{ L\pa{ \theta''_t, X} - L\pa{ \theta_t, X} }{\gamma} }, 1}$

On génére aléatoirement une variable $u \sim U\cro{0,1}$ , si $u \leqslant P_a$ , alors les paramètres $\theta''_t$ sont validés. $\hat{\theta}_t \longleftarrow \theta''_t$ et retour à l’étape d’expectation. Dans le cas contraire, les paramètres $\theta''_t$ sont refusés et retour à l’étape précédente.

terminaison

Si $t < T$ , on retoure à l’étape d’expectation, Sinon, on choisit les paramètres $\theta^*=\hat{\theta}_{t^*}$ qui maximisent l’expression :

(2)¶ $\begin{eqnarray} L\pa{\theta^* \sac X} &=& \log f \pa{X \sac \theta} - \frac{N^*}{2} \; \sum_{i=1}^{k^*} \log \frac{n \alpha_i^*}{12} - \frac{k^*}{2} \log \frac{n}{12} - \frac{k^*(N^*+1)}{2} \end{eqnarray}$

Avec $n$ le nombre d’exemples et $N$ est le nombre de paramètres spécifiant chaque composant.

L’article [ZhangB2004] prend $\gamma = 10$ mais ne précise pas de valeur pour $\beta$ qui dépend du problème. Toutefois, il existe un cas supplémentaire où la classe $m$ doit être supprimée afin d’éviter sa convergence vers les extrêmes du nuage de points à modéliser. Si $n \alpha_m < N$ , le nombre moyen de points inclus dans une classe est inférieur au nombre de paramètres attribués à cette classe qui est alors supprimée. Cette condition comme l’ensemble de l’article s’inspire de l’article [Figueiredo2002] dont est tiré le critère décrit en (ref{classif_cem_cirtere}).

Bibliographie¶

[Biernacki2001]

{Assessing a Mixture Model for Clustering with the Integrated Completed Likelihood (2001), C. Biernacki, G. Deleux, G. Govaert, IEEE Transactions on Image Analysis and Machine Intelligence, volume {22(7), pages 719-725

[Celeux1985]

The SEM algorithm: a probabilistic teacher algorithm derived from the EM algorithm for the mixture problem (1985), G. Celeux, J. Diebolt, Computational Statistics Quarterly, Volume 2(1), pages 73-82

[Celeux1985b]

On stochastic version of the EM algorithm (1985), Gilles Celeux, Didier Chauveau, Jean Diebolt, Rapport de recherche de l’INRIA*, n 2514

[Dempster1977]

Maximum-Likelihood from incomplete data via the EM algorithm (1977), A. P. Dempster, N. M. Laird, D. B. Rubin, Journal of Royal Statistical Society B, volume 39, pages 1-38

[Figueiredo2002]

Unsupervised learning of finite mixture models (2002), M. A. T. Figueiredo, A. K. Jain, IEEE Transactions on Pattern Analysis and Machine Intelligence, volume 24(3), pages 381-396

[ZhangB2004] (1,2,3)

Competitive EM algorithm for finite mixture models (2004), Baibo Zhang, Changshui Zhang, Xing Yi, Pattern Recognition, volume 37, pages 131-144