Régression quantile illustrée

La régression quantile est moins sensible aux points aberrants. Elle peut être définie comme une régression avec une norme L1 (une valeur absolue). Ce notebook explore des régressions avec des quantiles différents.

%matplotlib inline

Un jeu de données non symétrique

import numpy.random as npr
import numpy

n = 1000
eps = npr.normal(n)
X = npr.rand(n, 1) * 5
X1 = npr.normal(size=(n, 1)) * 1
X2 = npr.normal(size=(n // 2, 1)) * 10
X2 = numpy.vstack([X2, numpy.zeros((n // 2, 1))])
eps = -numpy.abs(X1) + numpy.abs(X2)
Y = (0.5 * X + eps).ravel()
X.shape, Y.shape

((1000, 1), (1000,))

import matplotlib.pyplot as plt

fig, ax = plt.subplots(1, 1, figsize=(5, 5))
ax.plot(X, Y, "c.");

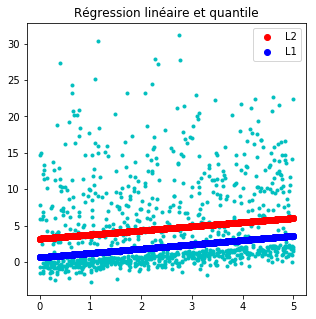
Régression linéaire et régression quantile

from sklearn.linear_model import LinearRegression

clr = LinearRegression()
clr.fit(X, Y)

LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)

from mlinsights.mlmodel import QuantileLinearRegression

clq = QuantileLinearRegression()
clq.fit(X, Y)

QuantileLinearRegression(copy_X=True, delta=0.0001, fit_intercept=True,
             max_iter=10, n_jobs=1, normalize=False, quantile=0.5,
             verbose=False)

fig, ax = plt.subplots(1, 1, figsize=(5, 5))
ax.plot(X, Y, "c.")
lin = clr.predict(X)
ax.plot(X, lin, "ro", label="L2")
qu = clq.predict(X)
ax.plot(X, qu, "bo", label="L1")
ax.legend()
ax.set_title("Régression linéaire et quantile");

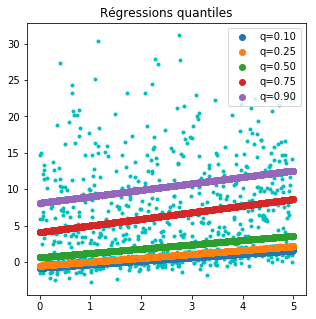
Différents quantiles

clqs = {}
for qu in [0.1, 0.25, 0.5, 0.75, 0.9]:
    clq = QuantileLinearRegression(quantile=qu)
    clq.fit(X, Y)
    clqs["q=%1.2f" % qu] = clq

fig, ax = plt.subplots(1, 1, figsize=(5, 5))
ax.plot(X, Y, "c.")
for k, v in sorted(clqs.items()):
    p = v.predict(X)
    ax.plot(X, p, "o", label=k)
ax.legend()
ax.set_title("Régressions quantiles");