Régression linéaire par morceaux

La régression linéaire par morceaux a l’avantage de produire un modèle localement interprétable. Mais ce n’est pas évident d’estimer un tel modèle quand on ne connaît pas les morceaux par avance.

%matplotlib inline

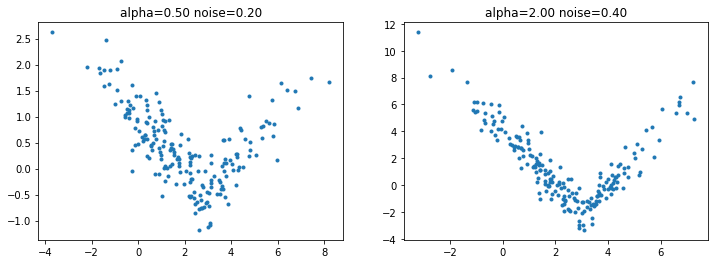
Des données artificielles

from numpy.random import normal
import numpy
import matplotlib.pyplot as plt


def nuage(n, alpha, noise=0.2):
    eps = normal(0, 2, (n, 2))
    X = eps[:, 0] + 2
    X1 = eps[:, 0].copy()
    X2 = eps[:, 0].copy()
    th = 1.0
    X1[th >= X1] = 0
    X2[th < X2] = 0
    sel = numpy.zeros((n,))
    sel[th < X1] = 1
    Y = X1 * alpha - X2 * alpha + eps[:, 1] * noise - sel * alpha * th * 2
    return X, Y


fig, ax = plt.subplots(1, 2, figsize=(12, 4))
alpha, noise = 0.5, 0.2
X, Y = nuage(200, alpha)
ax[0].plot(X, Y, ".")
ax[0].set_title("alpha=%1.2f noise=%1.2f" % (alpha, noise))
alpha, noise = 2.0, 0.4
X, Y = nuage(200, alpha, noise=0.4)
ax[1].plot(X, Y, ".")
ax[1].set_title("alpha=%1.2f noise=%1.2f" % (alpha, noise));

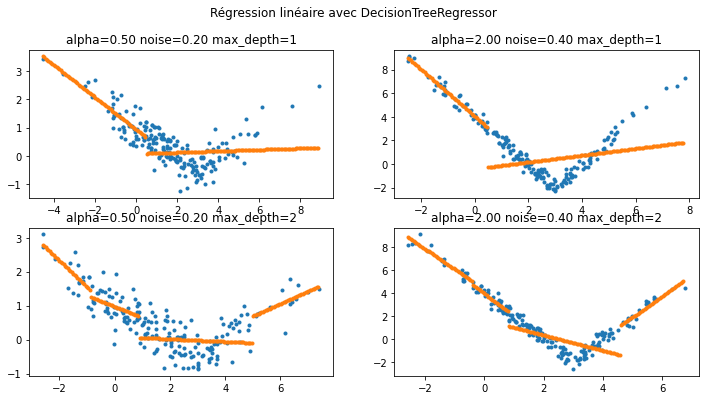
Quelques exemples avec un arbre de décision

La segmentation est réalisée d’abord avec un arbre de décision dont on fixe la profondeur. Chaque segment est choisi de telle sorte à minimiser l’approximation de la fonction par une constante sur chaque segment.

from mlinsights.mlmodel import PiecewiseRegressor
from sklearn.tree import DecisionTreeRegressor


def nuage_piecewise(n, alpha, noise=0.2, max_depth=1):
    X, Y = nuage(n, alpha, noise=noise)
    clr = PiecewiseRegressor(binner=DecisionTreeRegressor(max_depth=max_depth))
    Xm = X.reshape((len(X), 1))
    clr.fit(Xm, Y)
    mi, ma = X.min(), X.max()
    Xm = numpy.arange(0, 200) * (ma - mi) / 200 + mi
    Xm = Xm.reshape((len(Xm), 1))
    return X, Y, Xm, clr.predict(Xm)


def plot(i, j, alpha, noise, max_depth, ax):
    X, Y, XX, Z = nuage_piecewise(200, alpha, max_depth=max_depth)
    ax[i, j].plot(X, Y, ".")
    ax[i, j].plot(XX, Z, ".")
    ax[i, j].set_title(
        "alpha=%1.2f noise=%1.2f max_depth=%d" % (alpha, noise, max_depth)
    )


fig, ax = plt.subplots(2, 2, figsize=(12, 6))

alpha, noise, max_depth = 0.5, 0.2, 1
plot(0, 0, alpha, noise, max_depth, ax)

alpha, noise, max_depth = 2.0, 0.4, 1
plot(0, 1, alpha, noise, max_depth, ax)

alpha, noise, max_depth = 0.5, 0.2, 2
plot(1, 0, alpha, noise, max_depth, ax)

alpha, noise, max_depth = 2.0, 0.4, 2
plot(1, 1, alpha, noise, max_depth, ax)

plt.suptitle("Régression linéaire avec DecisionTreeRegressor");

Quelques exemples avec un KBinsDiscretizer

from sklearn.preprocessing import KBinsDiscretizer


def nuage_piecewise2(n, alpha, noise=0.2, n_bins=2):
    X, Y = nuage(n, alpha, noise=noise)
    clr = PiecewiseRegressor(binner=KBinsDiscretizer(n_bins=n_bins))
    Xm = X.reshape((len(X), 1))
    clr.fit(Xm, Y)
    mi, ma = X.min(), X.max()
    Xm = numpy.arange(0, 200) * (ma - mi) / 200 + mi
    Xm = Xm.reshape((len(Xm), 1))
    return X, Y, Xm, clr.predict(Xm)


def plot2(i, j, alpha, noise, n_bins, ax):
    X, Y, XX, Z = nuage_piecewise2(200, alpha, n_bins=n_bins)
    ax[i, j].plot(X, Y, ".")
    ax[i, j].plot(XX, Z, ".")
    ax[i, j].set_title("alpha=%1.2f noise=%1.2f n_bins=%d" % (alpha, noise, n_bins))


fig, ax = plt.subplots(2, 2, figsize=(12, 6))

alpha, noise, n_bins = 0.5, 0.2, 2
plot2(0, 0, alpha, noise, n_bins, ax)

alpha, noise, n_bins = 2.0, 0.4, 2
plot2(0, 1, alpha, noise, n_bins, ax)

alpha, noise, n_bins = 0.5, 0.2, 4
plot2(1, 0, alpha, noise, n_bins, ax)

alpha, noise, n_bins = 2.0, 0.4, 4
plot2(1, 1, alpha, noise, n_bins, ax)

plt.suptitle("Régression linéaire avec KBinsDiscretizer");

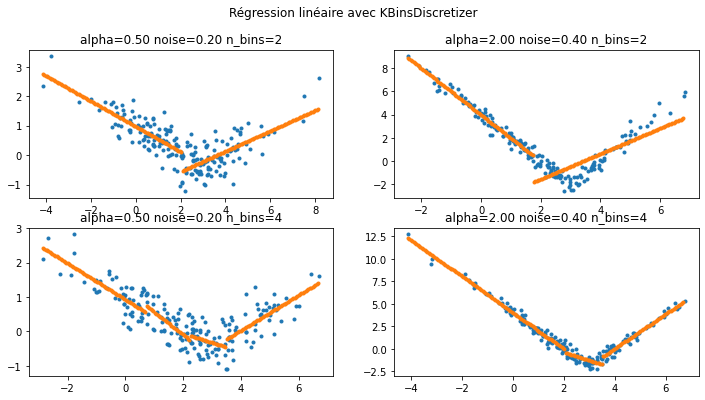
C’est mieux mais ce n’est pas parfait. La classe KBinsDiscretizer fonctionne simplement en segmentant les données mais elle ne tient pas compte de la cible.

Arbre de décision optimisé pour la régression linéaire

L’arbre suivant reprend l’algorithme de l’arbre de décision à ceci près qu’il optimise un critère MSE en approximant le nuage de points \((X_i, y_i)\) par une fonction linéaire \(y_i = X_i \beta + \epsilon_i\). Il faut néanmoins augmenter le nombre de points par feuille pour éviter quelques artefacts.

from mlinsights.mlmodel.piecewise_tree_regression import PiecewiseTreeRegressor


def nuage_piecewise3(n, alpha, noise=0.2, min_samples_leaf=30):
    X, Y = nuage(n, alpha, noise=noise)
    clr = PiecewiseTreeRegressor(criterion="mselin", min_samples_leaf=min_samples_leaf)
    Xm = X.reshape((len(X), 1))
    clr.fit(Xm, Y)
    mi, ma = X.min(), X.max()
    Xm = numpy.arange(0, 200) * (ma - mi) / 200 + mi
    Xm = Xm.reshape((len(Xm), 1))
    return X, Y, Xm, clr.predict(Xm)


def plot3(i, j, alpha, noise, min_samples_leaf, ax):
    X, Y, XX, Z = nuage_piecewise3(200, alpha, min_samples_leaf=min_samples_leaf)
    ax[i, j].plot(X, Y, ".")
    ax[i, j].plot(XX, Z, ".")
    ax[i, j].set_title(
        "alpha=%1.2f noise=%1.2f min_samples_leaf=%d" % (alpha, noise, min_samples_leaf)
    )


fig, ax = plt.subplots(2, 2, figsize=(12, 6))

alpha, noise, min_samples_leaf = 0.5, 0.2, 40
plot3(0, 0, alpha, noise, min_samples_leaf, ax)

alpha, noise, min_samples_leaf = 2.0, 0.4, 40
plot3(0, 1, alpha, noise, min_samples_leaf, ax)

alpha, noise, min_samples_leaf = 0.5, 0.2, 30
plot3(1, 0, alpha, noise, min_samples_leaf, ax)

alpha, noise, min_samples_leaf = 2.0, 0.4, 30
plot3(1, 1, alpha, noise, min_samples_leaf, ax)

plt.suptitle("Arbre de décision optimisé\npour la régression linéaire par morceaux");

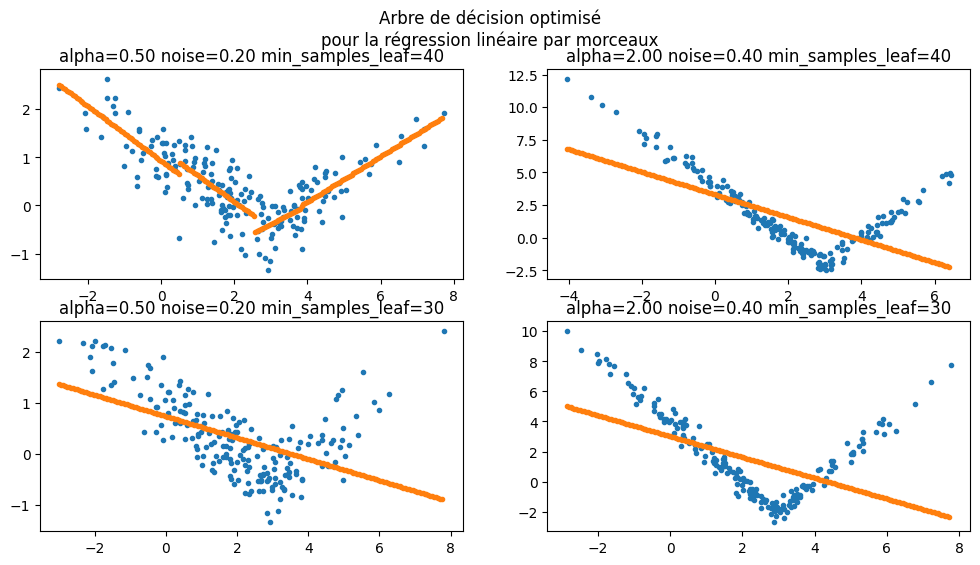
Il faudrait ajouter des contraintes de continuité.