Régression sans inversion

Ce notebook mesure le temps de calcul dans deux algorithmes pour résoudre une régression linéaire, le premier inverse un matrice, le second le fait sans inverser une matrice, le troisième reprend l’idée du second mais utilise une décomposition QR puis inverse la matrice R.

%matplotlib inline

import numpy.random as rnd

X = rnd.randn(1000, 7)
eps = rnd.randn(1000, 1) / 3
y = X.sum(axis=1).reshape((X.shape[0], 1)) + eps
y = y.ravel()
X.shape, y.shape, eps.shape

((1000, 7), (1000,), (1000, 1))

from mlstatpy.ml.matrices import linear_regression, gram_schmidt

beta1 = linear_regression(X, y, algo=None)
beta2 = linear_regression(X, y, algo="gram")
beta1, beta2

(array([0.97915374, 1.00078055, 1.00537618, 1.01021414, 1.0003261 ,
        0.9944518 , 0.98742625]),
 array([0.97915374, 1.00078055, 1.00537618, 1.01021414, 1.0003261 ,
        0.9944518 , 0.98742625]))

%timeit linear_regression(X, y, algo=None)

38.4 µs ± 2.07 µs per loop (mean ± std. dev. of 7 runs, 10000 loops each)

%timeit linear_regression(X, y, algo="gram")

310 µs ± 13.6 µs per loop (mean ± std. dev. of 7 runs, 1000 loops each)

%timeit linear_regression(X, y, algo="qr")

139 µs ± 8.29 µs per loop (mean ± std. dev. of 7 runs, 10000 loops each)

Xt = X.T
%timeit gram_schmidt(Xt)

210 µs ± 5.91 µs per loop (mean ± std. dev. of 7 runs, 1000 loops each)

Un exemple avec scikit-learn.

from sklearn.linear_model import LinearRegression

clr = LinearRegression()
%timeit clr.fit(X, y)

443 µs ± 48.3 µs per loop (mean ± std. dev. of 7 runs, 1000 loops each)

Qui utilise la fonction lstsq:

from numpy.linalg import lstsq

%timeit lstsq(X, y, rcond=None)

75.5 µs ± 2.57 µs per loop (mean ± std. dev. of 7 runs, 10000 loops each)

Il serait sans doute possible d’optimiser les calculs en réduisant le nombre de copie et de transposées. La version utilisant une décomposition QR est assez rapide. Le code est là matrices.py. Pour dépasser numpy, il faut passer au C++. scikit-learn ajoute des étapes intermédiaires pour vérifier les données ce qui explique la longueur. On résume le tout par un graphique.

from onnx_array_api.ext_test_case import measure_time

stmts = [
    dict(name="lr_matrix", fct="linear_regression(X, y, algo=None)"),
    dict(name="lr_gram", fct="linear_regression(X, y, algo='gram')"),
    dict(name="lr_qr", fct="linear_regression(X, y, algo='qr')"),
    dict(name="gram", fct="gram_schmidt(Xt)"),
    dict(name="sklearn", fct="clr.fit(X, y)"),
    dict(name="lstsq", fct="lstsq(X, y)"),
]

memo = []
for size, dim in [
    (100, 10),
    (1000, 10),
    (10000, 10),
    (100, 20),
    (1000, 20),
    (10000, 20),
    (100, 50),
    (1000, 50),
]:
    print(size, dim)
    X = rnd.randn(size, dim)
    eps = rnd.randn(size, 1) / 3
    y = X.sum(axis=1).reshape((X.shape[0], 1)) + eps
    y = y.ravel()
    context = dict(
        linear_regression=linear_regression,
        Xt=X.T,
        X=X,
        y=y,
        gram_schmidt=gram_schmidt,
        clr=clr,
        lstsq=lambda X, y: lstsq(X, y, rcond=None),
    )

    for stmt in stmts:
        res = measure_time(
            stmt["fct"], number=20, repeat=20, div_by_number=True, context=context
        )
        res.update(stmt)
        res["size"] = size
        res["dim"] = dim
        memo.append(res)

import pandas

df = pandas.DataFrame(memo)
df.head()

100 10
1000 10
10000 10
100 20
1000 20
10000 20
100 50
1000 50

	average	context_size	deviation	dim	fct	max_exec	min_exec	name	number	repeat	size
0	0.000039	368	0.000019	10	linear_regression(X, y, algo=None)	0.000091	0.000018	lr_matrix	20	20	100
1	0.000365	368	0.000045	10	linear_regression(X, y, algo='gram')	0.000485	0.000312	lr_gram	20	20	100
2	0.000114	368	0.000031	10	linear_regression(X, y, algo='qr')	0.000223	0.000093	lr_qr	20	20	100
3	0.000229	368	0.000020	10	gram_schmidt(Xt)	0.000256	0.000197	gram	20	20	100
4	0.000403	368	0.000031	10	clr.fit(X, y)	0.000464	0.000346	sklearn	20	20	100

piv = pandas.pivot_table(df, index=["size", "dim"], columns="name", values="average")
piv

	name	gram	lr_gram	lr_matrix	lr_qr	lstsq	sklearn
size	dim
100	10	0.000229	0.000365	0.000039	0.000114	0.000081	0.000403
	20	0.000442	0.000772	0.000057	0.000142	0.000143	0.000433
	50	0.001384	0.002303	0.000115	0.000298	0.000619	0.000935
1000	10	0.000335	0.000498	0.000052	0.000168	0.000140	0.000633
	20	0.000867	0.001197	0.000093	0.000335	0.000246	0.000641
	50	0.003242	0.004482	0.000263	0.001220	0.000945	0.001545
10000	10	0.001434	0.001309	0.000234	0.002760	0.000551	0.001828
	20	0.010212	0.010944	0.000293	0.005926	0.002128	0.005581

import matplotlib.pyplot as plt

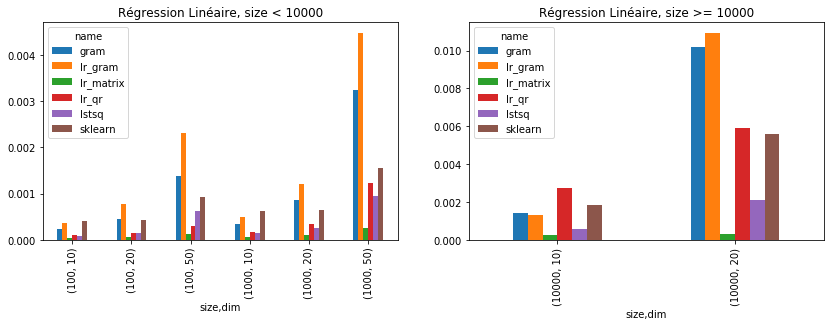
fig, ax = plt.subplots(1, 2, figsize=(14, 4))
piv[:6].plot(kind="bar", ax=ax[0])
piv[6:].plot(kind="bar", ax=ax[1])
ax[0].set_title("Régression Linéaire, size < 10000")
ax[1].set_title("Régression Linéaire, size >= 10000");

Streaming versions

L’idée est différente ici puisqu’il s’agit de calculer toutes les régressions linéaires intermédiaires. Les algorithmes sont décrits par l’exposé Régression linéaire par morceaux.

from mlstatpy.ml.matrices import (
    streaming_linear_regression,
    streaming_linear_regression_gram_schmidt,
)


def all_linear_regression(X, y):
    for i in range(X.shape[1], X.shape[0]):
        yield linear_regression(X[:i], y[:i])


stmts = [
    dict(name="lr_matrix", fct="list(all_linear_regression(X, y))"),
    dict(name="lr_st_mat", fct="list(streaming_linear_regression(X, y))"),
    dict(name="lr_st_gram", fct="list(streaming_linear_regression_gram_schmidt(X, y))"),
]

memo = []
for dim in (10,):
    for size in range(100, 3500, 500):
        print(size, dim)
        X = rnd.randn(size, dim)
        eps = rnd.randn(size, 1) / 3
        y = X.sum(axis=1).reshape((X.shape[0], 1)) + eps
        y = y.ravel()
        context = dict(
            X=X,
            y=y,
            all_linear_regression=all_linear_regression,
            streaming_linear_regression=streaming_linear_regression,
            streaming_linear_regression_gram_schmidt=streaming_linear_regression_gram_schmidt,
        )

        for stmt in stmts:
            if "gram" in stmt["name"]:
                nn = 1
                if size >= 1000:
                    continue
            else:
                nn = 5
            res = measure_time(
                stmt["fct"], number=nn, repeat=nn, div_by_number=True, context=context
            )
            res.update(stmt)
            res["size"] = size
            res["dim"] = dim
            memo.append(res)

import pandas

df = pandas.DataFrame(memo)
df.head()

100 10
600 10
1100 10
1600 10
2100 10
2600 10
3100 10

	average	context_size	deviation	dim	fct	max_exec	min_exec	name	number	repeat	size
0	0.002589	368	0.001263	10	list(all_linear_regression(X, y))	0.005070	0.001753	lr_matrix	5	5	100
1	0.002621	368	0.000038	10	list(streaming_linear_regression(X, y))	0.002688	0.002572	lr_st_mat	5	5	100
2	0.031022	368	0.000000	10	list(streaming_linear_regression_gram_schmidt(...	0.031022	0.031022	lr_st_gram	1	1	100
3	0.018594	368	0.000749	10	list(all_linear_regression(X, y))	0.019532	0.017664	lr_matrix	5	5	600
4	0.022098	368	0.001805	10	list(streaming_linear_regression(X, y))	0.024896	0.020070	lr_st_mat	5	5	600

piv = pandas.pivot_table(df, index=["size"], columns="name", values="average")
piv

name	lr_matrix	lr_st_gram	lr_st_mat
size
100	0.002589	0.031022	0.002621
600	0.018594	0.204768	0.022098
1100	0.040404	NaN	0.034072
1600	0.062186	NaN	0.052658
2100	0.097438	NaN	0.060824
2600	0.128451	NaN	0.079594
3100	0.161074	NaN	0.090113

fig, ax = plt.subplots(1, 2, figsize=(14, 4))
piv[["lr_matrix", "lr_st_mat"]].plot(ax=ax[0])
piv.plot(ax=ax[1])
ax[0].set_title("Régression Linéaire streaming (all)\n10 features")
ax[1].set_title("Régression Linéaire no Gram-Schmidt\n10 features");

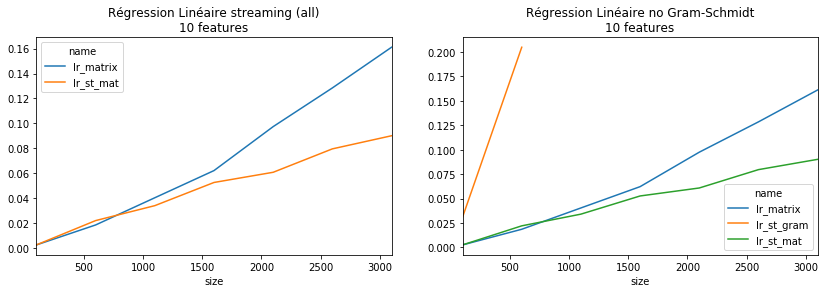
La version streaming devient plus intéressante à partir de 1000 observations, le coût en linéaire en N contrairement à la version classique qui est en \(N^2\). La version Gram-Schmidt devrait être réécrite en C++ pour proposer des temps comparables.