Démonstration du théorème de la densité des réseaux de neurones¶

Formulation du problème de la régression¶

Soient deux variables aléatoires continues $\pa{X,Y} \in \mathbb{R}^p \times \mathbb{R}^q \sim \loi$ quelconque, la résolution du problème de régression est l’estimation de la fonction $\esp(Y|X) = F\pa{X}$ . Pour cela, on dispose d’un ensemble de points $A = \acc{ \pa{X_{i},Y_{i}} \sim \loi | 1 \leqslant i \leqslant N }$ .

Soit $f : \mathbb{R}^M \times \mathbb{R}^p \longrightarrow \mathbb{R}^q$ une fonction, on définit $\forall i \in \intervalle{1}{N}, \; \widehat{Y_{i}^{W}} = f \pa{W,X_{i}}$ . On appelle aussi $\widehat{Y_{i}^{W}}$ la valeur prédite pour $X_{i}$ . On pose alors $\epsilon_{i}^{W} = Y_{i} - \widehat{Y_{i}^{W}} = Y_{i} - f \pa{W,X_{i}}$ .

Les résidus sont supposés i.i.d. (identiquement et indépendemment distribués), et suivant une loi normale $\forall i \in \intervalle{1}{N}, \; \epsilon_{i}^{W} \sim \loinormale{\mu_{W}}{\sigma_{W}}$ La vraisemblance d’un échantillon $\pa{Z_i}_{1\leqslant i \leqslant N}$ , où les $Z_i$ sont indépendantes entre elles et suivent la loi de densité $f \pa{z | \theta}$ est la densité du vecteur $\vecteur{Z_1}{Z_N}$ qu’on exprime comme suit :

$\begin{array}{rrcl} &L\pa{\theta, \vecteurno{Z_1}{Z_N}} & =& \prod_{n=1}^{N} f\pa{Z_i | \theta} \\ \Longrightarrow& \ln L\pa{\theta, \vecteurno{Z_1}{Z_N}} &=& \sum_{n=1}^{N} \ln f\pa{Z_i | \theta} \end{array}$

La log-vraisemblance de l’échantillon s’écrit $L_{W} = -\frac{1}{2\sigma_{W}^2} \sum_{i=1}^{N} \pa{Y_{i} - \widehat{Y_{i}^W} - \mu_{W} }^2 + N\ln\pa{\sigma_{W}\sqrt{2\pi}}$ . Les estimateurs du maximum de vraisemblance pour $\mu_W$ et $\sigma_W$ sont (voir [Saporta1990]) :

$\begin{array}{rcl} \widehat{\mu_{W}} &=& \frac{1}{N} \sum_{i=1}^{N} Y_{i} - \widehat{Y_{i}^W} \\ \widehat{\sigma_{W}} &=& \sqrt{ \frac{ \sum_{i=1}^{N} \pa{Y_{i} - \widehat{Y_{i}^W} - \mu_{W}}^2}{N}} \end{array}$

L’estimateur de $\widehat{Y}=f\pa{W,X}$ désirée est de préférence sans biais ( $\mu_W = 0$ ) et de variance minimum, par conséquent, les paramètres $\overset{*}{W}$ qui maximisent la vraisemblance $L_W$ sont :

(1)¶ $\begin{array}{rcl} \overset{*}{W} &=& \underset{W \in \mathbb{R}^M}{\arg \min} \sum_{i=1}^{N} \pa {Y_{i} - \widehat{Y_{i}^W}}^2 \\ &=& \underset{W \in \mathbb{R}^M}{\arg \min} \sum_{i=1}^{N} \pa {Y_{i} - f \pa{W,X_{i}}}^2 \end{array}$

Réciproquement, on vérifie que si $W^*$ vérifie l’équation (1) alors l’estimateur défini par $f$ est sans biais Il suffit pour s’en convaincre de poser $g = f + \alpha$ avec $\alpha \in \mathbb{R}$ et de vérifier que la valeur optimale pour $\alpha$ est $\alpha = - \frac{1}{N}\, \sum_{i=1}^{N} \, \left. Y_i - f\pa{W,X_i} \right.$ . L’estimateur minimise la vraisemblance $L_W$ . Cette formule peut être généralisée en faisant une autre hypothèse que celle de la normalité des résidus (l’indépendance étant conservée), l’équation (1) peut généralisée par (2).

(2)¶ $\begin{array}{rcl} \overset{*}{W} &=& \underset{W \in \mathbb{R}^M}{\arg \min} \sum_{i=1}^{N} e\pa {Y_{i} - \widehat{Y_{i}^W}} \\ &=& \underset{W \in \mathbb{R}^M}{\arg \min} \sum_{i=1}^{N} e\pa{Y_{i} - f \pa{W,X_{i}}} \end{array}$

Où la fonction $e : \mathbb{R}^q \in \mathbb{R}$ est appelée fonction d’erreur.

Densité des réseaux de neurones¶

L’utilisation de réseaux de neurones s’est considérablement développée depuis que l’algorithme de rétropropagation a été trouvé ([LeCun1985], [Rumelhart1986], [Bishop1995]). Ce dernier permet d’estimer la dérivée d’un réseau de neurones en un point donné et a ouvert la voie à des méthodes classiques de résolution pour des problèmes d’optimisation tels que la régression non linéaire.

Comme l’ensemble des fonctions polynômiales, l’ensemble des fonctions engendrées par des réseaux de neurones multi-couches possède des propriétés de densité et sont infiniment dérivables. Les réseaux de neurones comme les polynômes sont utilisés pour modéliser la fonction $f$ de l’équation (2). Ils diffèrent néanmoins sur certains points

Si une couche ne contient que des fonctions de transfert bornées comme la fonction sigmoïde, tout réseau de neurones incluant cette couche sera aussi borné. D’un point de vue informatique, il est préférable d’effectuer des calculs avec des valeurs du même ordre de grandeur. Pour un polynôme, les valeurs des termes de degré élevé peuvent être largement supérieurs à leur somme.

Un autre attrait est la symétrie dans l’architecture d’un réseau de neurones, les neurones qui le composent jouent des rôles symétriques (corollaire familles libres. Pour améliorer l’approximation d’une fonction, dans un cas, il suffit d’ajouter un neurone au réseau, dans l’autre, il faut inclure des polynômes de degré plus élevé que ceux déjà employés.

Théorème T1 : densité des réseaux de neurones (Cybenko1989)

[Cybenko1989] Soit $E_{p}^{q}$ l’espace des réseaux de neurones à $p$ entrées et $q$ sorties, possédant une couche cachée dont la fonction de seuil est une fonction sigmoïde $\left( x\rightarrow 1-\frac{2}{1+e^{x}}\right)$ , une couche de sortie dont la fonction de seuil est linéaire Soit $F_{p}^{q}$ l’ensemble des fonctions continues de $C\subset\mathbb{R}^{p}\longrightarrow\mathbb{R}^{q}$ avec $C$ compact muni de la norme $\left\| f\right\| =\underset{x\in C}{\sup}\left\| f\left( x\right) \right\|$ Alors $E_{p}^{q}$ est dense dans $F_{p}^{q}$ .

La démonstration de ce théorème nécessite deux lemmes. Ceux-ci utilisent la définition usuelle du produit scalaire sur $\mathbb{R}^p$ défini par $\pa{x,y} = \pa{\vecteurno{x_1}{x_p},\vecteurno{y_1}{y_p}} \in \mathbb{R}^{2p} \longrightarrow \left\langle x,y \right\rangle = \sum_{i=1}^{p} x_i y_i$ . et la norme infinie : $x = \vecteur{x_1}{x_p} \in \mathbb{R}^p \longrightarrow \norm{x} = \underset{i \in \intervalle{1}{p}}{\max} x_i$ . Toutes les normes sont équivalentes sur $\mathbb{R}^p$ .

Corollaire C1 : approximation d’une fonction créneau

Soit $C \subset \mathbb{R}^p, \; C= \acc { \vecteur{y_1}{y_p} \in \mathbb{R}^p \, | \forall i\in \intervalle{1}{p},\, 0 \leqslant y_{i}\leqslant 1 }$ , alors :

$\begin{array}{l} \forall \varepsilon > 0, \; \forall \alpha>0, \; \exists n \in \N^*, \; \exists \vecteur{x_1}{x_n} \in\left( \mathbb{R}^p\right) ^{n}, \; \exists \vecteur{\gamma_1}{\gamma_n} \in \mathbb{R}^n \text{ tels que } \forall x\in \mathbb{R}^p, \\ \\ \begin{array}{ll} & \left| \underset{i=1}{\overset{n}{\sum}}\dfrac{\gamma_i} {1+e^{\left\langle x_{i},x\right\rangle +b_{i}}}-\indicatrice{x\in C }\right| \leqslant1 \\ \\ \text{ et } & \underset{y\in Fr\left( C\right) }{\inf }\left\| x-y\right\| > \alpha\mathbb{R}ightarrow\left| \underset{i=1}{\overset {n}{\sum}}\dfrac{\gamma_i}{1+e^{\left\langle x_{i},x\right\rangle +b_{i}}} -\indicatrice{x\in C}\right| \leqslant\varepsilon \end{array} \end{array}$

Démonstration du corollaire

Partie 1

Soit $h$ la fonction définie par : $h\pa{x} = \pa{\dfrac{1}{1+e^{-kx}}}^p$ avec $p>0$ et $0 < \epsilon < 1$ . A $\alpha$ , $\epsilon$ fixé, $0 < \epsilon < 1$ , on cherche $k$ tel que :

$\begin{array}{crcl} & \epsilon &=& h\pa{\alpha} = \pa{\dfrac{1}{1+e^{-k\alpha}}}^p \\ \Longrightarrow & \epsilon^{-\frac{1}{p}} &=& 1+e^{-k\alpha} \\ \Longrightarrow & \epsilon^{-\frac{1}{p}} -1 &=& e^{-k\alpha} \\ \Longrightarrow & \ln \pa{\epsilon^{-\frac{1}{p}} -1} &=& -k\alpha \\ \Longrightarrow & k &=& - \dfrac{ \ln\pa{\epsilon^{-\frac{1}{p}} -1}}{\alpha} = k_0\pa{\epsilon,\alpha,p} \end{array}$

Partie 2

Soit $\alpha>0$ et $1\geqslant\varepsilon>0, \, k>0$ ,

On pose $f\left( y_{1},...,y_{p}\right) =\underset{i=1}{\overset{p}{\prod}} \dfrac{1}{1+e^{-ky_{i}}}\underset{i=1}{\overset{p}{\prod}}\dfrac {1}{1+e^{-k\left( 1-y_{i}\right)}}$ d’après sa définition, $0 \leqslant f\left( y_{1},...,y_{p}\right) \leqslant 1$ .

Pour $k \supegal k_0 \pa{\epsilon,\alpha,2p}$ obtenu dans la partie précédente :

$\underset{_{i\in\left\{ 1,...,p\right\}}}{\inf} \cro { \min\left\{ \left| y_{i}\right| ,\left| 1-y_{i}\right| \right\} } >\alpha \Longrightarrow\left\| f\left( y_{1},...,y_{p}\right) - \indicatrice{x\in C}\right\| \leqslant\varepsilon$

Partie 3

Soit $g$ la fonction définie par :

$\begin{array}{rcl} g\pa{x} &=& \pa{\dfrac{1}{1+e^{-kx}}}\pa{\dfrac{1}{1+e^{-k\pa{1-x}}}} = \dfrac{1}{1+e^{-kx}+e^{-k\pa{1-x}}+e^{-k}} \\ &=& \dfrac{1}{1+e^{-kx}+e^{-k}e^{kx}+e^{-k}} = \dfrac{e^{kx}}{e^{kx}\pa{1+e^{-k}}+1+e^{-k}e^{2kx}} \end{array}$

La fonction $x \longrightarrow e^{kx}\pa{1+e^{-k}}+1+e^{-k}e^{2kx}$ est un polynôme en $e^{kx}$ dont le discriminant est positif. Par conséquent la fraction rationnelle $g\pa{x}$ admet une décomposition en éléments simples du premier ordre et il existe quatre réels $\eta_1$ , $\eta_2$ , $\delta_1$ , $\delta_2$ tels que :

$g\pa{x} = \dfrac{\eta_1}{1+ e^{kx+\delta_1}} + \dfrac{\eta_2}{1+ e^{kx+\delta_2}}$

Par conséquent :

$f\vecteur{y_1}{y_p} = \prod_{i=1}^{p} g\pa{y_i} = \prod_{i=1}^{p} \cro { \dfrac{\eta_1^i}{1+ e^{ky_i+\delta_1^i}} + \dfrac{\eta_2^i}{1+ e^{ky_i+\delta_2^i}} }$

Il existe $n \in \N$ tel qu’il soit possible d’écrire $f$ sous la forme :

$f\pa{y} = \sum_{i=1}^{n} \dfrac{\gamma_i}{ 1 + e^{ <x_i,y> + b_i } }$

Corollaire C2 : approximation d’une fonction indicatrice

Soit $C\subset\mathbb{R}^p$ compact, alors :

$\begin{array}{c} \forall\varepsilon>0, \; \forall\alpha>0, \; \exists\left( x_{1},...,x_{n}\right) \in\left( \mathbb{R}^{p}\right)^{n}, \; \exists\left( b_{1},...,b_{n}\right) \in\mathbb{R}^n \text{ tels que } \forall x\in\mathbb{R}^{p},\\ \\ \begin{array}{ll} & \left| \sum_{i=1}^n \dfrac{\gamma_i} {1+e^{\left\langle x_{i},x\right\rangle +b_{i}}}-\indicatrice{x\in C }\right| \leqslant1+2\varepsilon^2\\ \\ \text{ et } & \underset{y\in Fr\left( C\right) }{\inf}\left\| x-y\right\| >\alpha\mathbb{R}ightarrow\left| \sum_{i=1}^n \dfrac{\gamma_i}{1+e^{\left\langle x_{i} ,x\right\rangle +b_{i}}}- \indicatrice{x\in C}\right| \leqslant \varepsilon \end{array} \end{array}$

Démonstration du corollaire

Partie 1

Soit $C_1=\left\{ y=\left( y_{1},...,y_{p}\right) \in\mathbb{R}^p \,\left| \, \forall i\in\left\{ 1,...,n\right\} ,\,0\leqslant y_{i}\leqslant1\right. \right\}$ et $C_{2}^{j}=\left\{ y=\left( y_{1},...,y_{p}\right) \in\mathbb{R}^p\,\left| \, \forall i\neq j,\,0\leqslant y_{i}\leqslant1 \text{ et }1\leqslant y_{j}\leqslant2\right. \right\}$

Le premier lemme suggère que la fonction cherchée pour ce lemme dans le cas particulier $C_1\cup C_2^j$ est :

$\begin{array}{rcl} f\left( y_{1},...,y_{p}\right) &=& \prod_{i=1}^p \dfrac {1}{1+e^{-ky_{i}}} \prod_{i=1}^p\dfrac{1}{1+e^{-k\left( 1-y_{i}\right) }}+ \\ && \quad \left( \prod_{i \neq j} \dfrac {1}{1+e^{-ky_{i}}}\right) \left( \prod_{i \neq j} \dfrac{1}{1+e^{-k\left( 1-y_{i}\right) }}\right) \dfrac{1}{1+e^{k\left( 1-y_{j}\right) }}\dfrac{1}{1+e^{-k\left( 2-y_{j}\right) }}\\ % &=& \left( \prod_{i \neq j} \dfrac{1}{1+e^{-ky_{i}}}\right) \left( \prod_{i \neq j} \dfrac{1}{1+e^{-k\left( 1-y_{i}\right) }}\right) \\ && \quad \left( \dfrac{1}{1+e^{-ky_{j}}}\dfrac{1}{1+e^{-k\left( 1-y_{j}\right) }} +\dfrac {1}{1+e^{k\left( 1-y_{j}\right) }} \dfrac{1}{1+e^{-k\left(2-y_{j}\right) }}\right) \\ % &=& \left( \prod_{i \neq j} \dfrac{1}{1+e^{-ky_{i}}}\right) \left( \prod_{i \neq j} \dfrac{1}{1+e^{-k\left( 1-y_{i}\right) }}\right) \\ && \quad \left[\dfrac{1}{1+e^{-ky_{j}}}\left( \dfrac{1}{1+e^{-k\left( 1-y_{j}\right) } }+1-1\right) +\left( 1-\dfrac{1}{1+e^{-k\left( 1-y_{j}\right) }}\right) \dfrac{1}{1+e^{-k\left( 2-y_{j}\right) }}\right] \end{array}$

Pour $k \supegal k_0\pa{\epsilon,\alpha,2p}$ , on a :

$\begin{array}{rcl} f\left( y_{1},...,y_{p}\right) &=& \left( \prod_{i\neq j} \dfrac{1}{1+e^{-ky_{i}}}\right) \left( \prod_{i\neq j} \dfrac{1}{1+e^{-k\left( 1-y_{i}\right) }}\right) \\ && \quad \left( \dfrac{1}% {1+e^{-ky_{j}}}+\dfrac{1}{1+e^{-k\left( 2-y_{j}\right) }}+ \underset {\leqslant\varepsilon^{2}}{\underbrace{\dfrac{1}{1+e^{k\left( 1-y_{j}\right) }}\dfrac{1}{1+e^{-ky_{j}}}}}-\underset{\leqslant\varepsilon^{2}}% {\underbrace{\dfrac{1}{1+e^{-k\left( 1-y_{j}\right) }}\dfrac{1}% {1+e^{-k\left( 2-y_{j}\right) }}}}\right) \end{array}$

Par conséquent, il est facile de construire la fonction cherchée pour tout compact connexe par arc.

Partie 2

Si un compact $C$ n’est pas connexe par arc, on peut le recouvrir par une somme finie de compacts connexes par arcs et disjoints $\left(C_{k}\right) _{1\leqslant k\leqslant K}$ de telle sorte que :

$\forall y\in\underset{k=1}{\overset{K}{\cup}}C_{k},\,\inf\left\{ \left\| x-y\right\| ,\,x\in C\right\} \leqslant\dfrac{\alpha}{2}$

Démontration du théorème de densité des réseaux de neurones

Partie 1

On démontre le théorème dans le cas où $q=1$ . Soit $f$ une fonction continue du compact $C\subset\mathbb{R}^p\rightarrow \mathbb{R}$ et soit $\varepsilon>0$ .

On suppose également que $f$ est positive, dans le cas contraire, on pose $f=\underset{\text{fonction positive}}{\underbrace{f-\inf f}}+\inf f$ .

Si $f$ est nulle, alors c’est fini, sinon, on pose $M=\underset{x\in C}{\sup }f\left( x\right)$ . $M$ existe car $f$ est continue et $C$ est compact (de même, $\inf f$ existe également).

On pose $C_{k}=f^{-1}\left( \left[ k\varepsilon,M\right] \right)$ . $C_k$ est compact car il est l’image réciproque d’un compact par une fonction continue et $C_k\subset C$ compact.

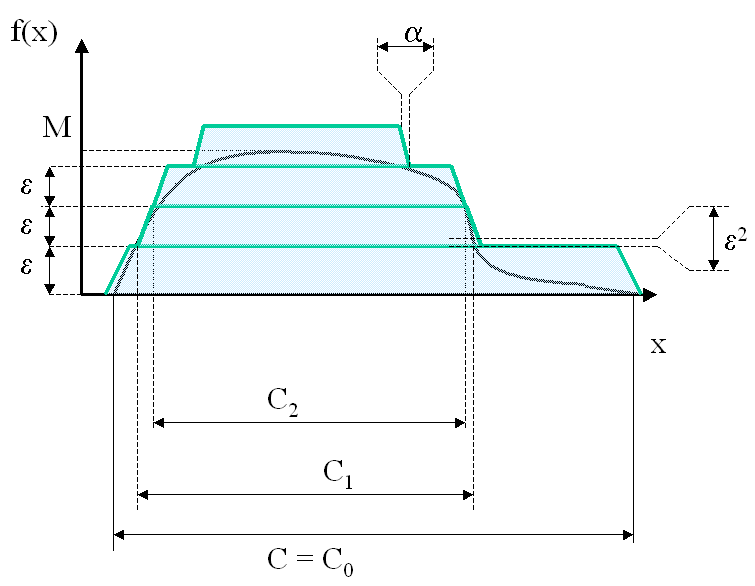
Par construction, $C_{k+1}\subset C_{k}$ et $C=\underset{k=0}{\overset {\frac{M}{\varepsilon}} {\bigcup}}C_{k}=C_{0}$ on définit~:

$\forall x\in C,\; g_{\varepsilon}\left( x\right) = \varepsilon\overset{\frac {M}{\varepsilon}}{ \sum_{k=0}}\indicatrice{x\in C_{k}}$

D’où~:

$\begin{eqnarray} f\left( x\right) -g_{\varepsilon}\left( x\right) &=& f\left( x\right)-\varepsilon\overset{\frac{M}{\varepsilon}}{\sum_{k=0}} \indicatrice{x\in C_{k}} \nonumber = f\left( x\right) -\varepsilon \overset{\frac{M}{\varepsilon}} {\sum_{k=0}}\indicatrice { f\pa{x} \supegal k \varepsilon } \nonumber \\ &=& f\left( x\right) -\varepsilon\left[ \dfrac{f\left( x\right) } {\varepsilon}\right] \quad \text{ (partie entière)}\nonumber \\ & \text{d'où }& 0\leqslant f\left( x\right) -g_{\varepsilon}\left( x\right) \leqslant \frac{\varepsilon}{4} \end{eqnarray}$

Comme $f$ est continue sur un compact, elle est uniformément continue sur ce compact :

$\begin{array}{l} \exists\alpha>0 \text{ tel que } \forall\left( x,y\right) \in C^{2}, \; \left\| x-y\right\| \leqslant\alpha\Longrightarrow\left| f\left( x\right) -f\left( y\right) \right| \leqslant \frac{ \varepsilon}{2} \\ \\ \text{ d'où } \left| f\left( x\right) -f\left( y\right) \right| \supegal \varepsilon \Longrightarrow\left\| x-y\right\| >\alpha \end{array}$

Par conséquent :

$\inf\left\{ \left\| x-y\right\| \,\left| \,x\in Fr\left( C_{k}\right) ,\,y\in Fr\left( C_{k+1}\right) \right. \right\} >\alpha$

D’après le second lemme, on peut construire des fonctions $h_{k}\left( x\right) =\sum_{i=1}^n\dfrac{1}{1+e^{\left\langle x_{i}^{k},x\right\rangle +b_{i}^{k}}}$ telles que :

$\left( \left\| h_{k}\left( x\right) -\indicatrice{x\in C_{k}}\right\| \leqslant1 \right) \text{ et } \left( \underset{y\in Fr\left( C\right) }{\inf}\left\| x-y\right\| >\dfrac{\alpha}{2}% \mathbb{R}ightarrow\left\| h_{k}\left( x\right) -\indicatrice{x\in C_{k}}\right\| \leqslant\varepsilon^{2}\right)$

On en déduit que :

$\begin{array}{rcl} \left| f\left( x\right) -\varepsilon\overset{\frac{M}{\varepsilon}} {\sum_{k=0}}h_{k}\left( x\right) \right| &\leqslant& \left| f\left( x\right) -g_{\varepsilon}\left( x\right) \right| +\left|g_{\varepsilon}\left( x\right) -\varepsilon \overset{\frac{M}{\varepsilon}}{\sum_{k=0}}h_{k}\left( x\right) \right| \\ &\leqslant& \varepsilon+ \varepsilon^2 \left[ \dfrac{M}{\varepsilon}\right] + 2\varepsilon^2 \\ &\leqslant& \varepsilon\left( M+3\right) \end{array}$

Comme $\varepsilon\overset{\frac{M}{\varepsilon}}{\sum_{k=1}} h_{k}\left( x\right)$ est de la forme désirée, le théorème est démontré dans le cas $q=1$ .

Partie 2

Dans le cas $q>1$ , on utilise la méthode précédente pour chacune des projections de $f$ dans un repère orthonormé de $\mathbb{R}^{q}$ . Il suffit de sommer sur chacune des dimensions.

Ce théorème montre qu’il est judicieux de modéliser la fonction $f$ dans l’équation (2) par un réseau de neurones puisqu’il possible de s’approcher d’aussi près qu’on veut de la fonction $\esp\pa{Y | X}$ , il suffit d’ajouter des neurones sur la couche cachée du réseau. Ce théorème permet de déduire le corollaire suivant :

Corollaire C3 : famille libre de fonctions

Soit $F_{p}$ l’ensemble des fonctions continues de $C\subset\mathbb{R}^{p}\longrightarrow\mathbb{R}$ avec $C$ compact muni de la norme : $\left\| f\right\| =\underset{x\in C}{\sup}\left\| f\left( x\right) \right\|$ Alors l’ensemble $E_{p}$ des fonctions sigmoïdes :

$E_{p} = \acc{ x \longrightarrow 1 - \dfrac{2}{1 + e^{<y,x>+b}} | y \in \mathbb{R}^p \text{ et } b \in \mathbb{R}}$

est une base de $F_{p}$ .

Démonstration du corollaire

Le théorème de densité montre que la famille $E_{p}$ est une famille génératrice. Il reste à montrer que c’est une famille libre. Soient $\pa{y_i}_{1 \leqslant i \leqslant N} \in \pa{\mathbb{R}^p}^N$ et $\pa{b_i}_{1 \leqslant i \leqslant N} \in \mathbb{R}^N$ vérifiant : $i \neq j \Longrightarrow y_i \neq y_j \text{ ou } b_i \neq b_j$ . Soit $\pa{\lambda_i}_{1 \leqslant i \leqslant N} \in \mathbb{R}^N$ , il faut montrer que :

(3)¶ $\begin{eqnarray} \forall x \in \mathbb{R}^p, \; \sum_{i=1}^{N} \lambda_i \pa{ 1 - \dfrac{2}{1 + e^{<y_i,x>+b_i} }} = 0 \Longrightarrow \forall i \, \lambda_i = 0 \end{eqnarray}$

C’est évidemment vrai pour $N=1$ . La démonstration est basée sur un raisonnement par récurrence, on suppose qu’elle est vraie pour $N-1$ , démontrons qu’elle est vraie pour $N$ . On suppose donc $N \supegal 2$ . S’il existe $i \in \ensemble{1}{N}$ tel que $y_i = 0$ , la fonction $x \longrightarrow 1 - \dfrac{2}{1 + e^{<y_i,x>+b_i}}$ est une constante, par conséquent, dans ce cas le corollaire est est vrai pour $N$ . Dans le cas contraire, $\forall i \in \ensemble{1}{N}, \; y_i \neq 0$ . On définit les vecteurs $X_i = \pa{x_i,1}$ et $Y_i = \pa{y_j, b_j}$ . On cherche à résoude le système de $N$ équations à $N$ inconnues :

(4)¶ $\begin{eqnarray} \left\{ \begin{array}{ccc} \sum_{j=1}^{N} \lambda_j \pa{ 1 - \dfrac{2}{1 + e^{<Y_j,X_1>}}} &=& 0 \\ \ldots \\ \sum_{j=1}^{N} \lambda_j \pa{ 1 - \dfrac{2}{1 + e^{<Y_j,X_i>}}} &=& 0 \\ \ldots \\ \sum_{j=1}^{N} \lambda_j \pa{ 1 - \dfrac{2}{1 + e^{<Y_j,X_N>}}} &=& 0 \end{array} \right. \end{eqnarray}$

On note le vecteur $\Lambda = \pa{\lambda_i}_{ 1 \leqslant i \leqslant N}$ et $M$ la matrice :

$M= \pa{m_{ij}}_{ 1 \leqslant i,j \leqslant N} = \pa{ 1 - \dfrac{2}{1 + e^{<Y_j,X_i>}} }_{ 1 \leqslant i,j \leqslant N}$

L’équation (4) est équivalente à l’équation matricielle : $M\Lambda = 0$ . On effectue une itération du pivot de Gauss. (4) équivaut à :

$\begin{array}{rcl} &\Longleftrightarrow& \left\{ \begin{array}{ccllllllll} \lambda_1 m_{11} &+& \lambda_2 & m_{12} &+& \ldots &+& \lambda_N & m_{1N} & = 0 \\ 0 &+& \lambda_2 & \pa{ m_{22} m_{11} - m_{12} m_{21} } &+& \ldots &+& \lambda_N & \pa{ m_{2N} m_{11} - m_{1N} m_{21} } & = 0 \\ \ldots \\ 0 &+& \lambda_2 & \pa{ m_{N2} m_{11} - m_{12} m_{N1} } &+& \ldots &+& \lambda_N & \pa{ m_{NN} m_{11} - m_{1N} m_{N1} } & = 0 \end{array} \right. \end{array}$

On note $\Lambda_* = \pa{\lambda_i}_{ 2 \leqslant i \leqslant N}$ et $\Delta_*$ , $M_*$ les matrices :

$\begin{array}{rcl} M_* &=& \pa{m_{ij}}_{ 2 \leqslant i,j \leqslant N} \\ \Delta_* &=& \pa{ m_{1j} \, m_{i1} }_{ 2 \leqslant i,j \leqslant N} \end{array}$

Donc (4) est équivalent à :

(5)¶ $\begin{eqnarray} \begin{array}{ccl} &\Longleftrightarrow& \left\{ \begin{array}{cccc} \lambda_1 m_{11}&+& \lambda_2 m_{12} + \ldots + \lambda_N m_{1N} &= 0 \\ 0 &+& \pa{ m_{11} M_* - \Delta_*} \Lambda_* & = 0 \end{array} \right. \end{array} \end{eqnarray}$

Il est possible de choisir $X_1\pa{\alpha} = \pa{\alpha x_1, 1}$ de telle sorte qu’il existe une suite $\pa{s_l}_{ 1 \leqslant l \leqslant N } \in \acc{-1,1}^{N}$ avec $s_1=1$ et vérifiant :

$\forall j \in \vecteur{1}{N}, \; \underset{\alpha \longrightarrow +\infty} {\lim } \cro{ 1 - \dfrac{2}{1 + e^{<Y_j, \, X_1\pa{\alpha} >}} } = \underset{\alpha \longrightarrow +\infty} {\lim } m_{1j}\pa{\alpha} = s_j$

On définit :

$\begin{array}{rll} U_* &=& \vecteur{m_{21}}{m_{N1}}' \\ V_* &=& \vecteur{s_2 \, m_{21}}{s_N \, m_{N1}}' \\ \text{ et la matrice } L_* &=& \pa{V_*}_ { 2 \leqslant i \leqslant N } \text{ dont les $N-1$ colonnes sont identiques } \end{array}$

On vérifie que :

$\underset{\alpha \longrightarrow +\infty} {\lim } \Delta\pa{\alpha} = V_*$

On obtient, toujours pour (4) :

(6)¶ $\begin{eqnarray} &\Longleftrightarrow& \left\{ \begin{array}{cclc} \lambda_1 m_{11}\pa{\alpha} &+& \lambda_2 m_{12}\pa{\alpha} + \ldots + \lambda_N m_{1N}\pa{\alpha} &= 0 \\ 0 &+& \cro{m_{11}\pa{\alpha} M_* - \pa{ L_* + \pa{ \Delta_*\pa{\alpha} - L_* } } } \Lambda_* & = 0 \end{array} \right. \\ \nonumber\\ &\Longleftrightarrow& \left\{ \begin{array}{cclc} \lambda_1 m_{11}\pa{\alpha} &+& \lambda_2 m_{12}\pa{\alpha} + \ldots + \lambda_N m_{1N}\pa{\alpha} &= 0 \\ 0 &+& \pa{m_{11}\pa{\alpha} M_* - L_* } \Lambda_* + \pa{ \Delta_*\pa{\alpha} - L_* } \Lambda_* & = 0 \end{array} \right. \nonumber \end{eqnarray}$

On étudie la limite lorsque $\alpha \longrightarrow +\infty$ :

$\begin{array}{crcl} & \pa{ \Delta_*\pa{\alpha} - L_* } & \underset{ \alpha \rightarrow +\infty}{ \longrightarrow} & 0 \\ \Longrightarrow & \pa{m_{11}\pa{\alpha} M_* - L_* } \Lambda_* & \underset{ \alpha \rightarrow +\infty}{ \longrightarrow} & 0\\ \Longrightarrow & \pa{M_* - L_* } \Lambda_* & = & 0\\ \Longrightarrow & M_* \Lambda_* - \pa{ \sum_{j=2}^{N} \lambda_j } V_* & = & 0\\ \end{array}$

Donc :

(7)¶ $\begin{eqnarray*} M_* \Lambda_* - \pa{ \sum_{j=2}^{N} \lambda_j } V_* &=& 0 \end{eqnarray*}$

D’après l’hypothèse de récurrence, (7) implique que : $\forall i \in \ensemble{2}{N}, \; \lambda_i = 0$ . Il reste à montrer que $\lambda_1$ est nécessairement nul ce qui est le cas losque $\alpha \longrightarrow +\infty$ , alors $\lambda_1 m_{11}\pa{\alpha} \longrightarrow \lambda_1 = 0$ . La récurrence est démontrée.

A chaque fonction sigmoïde du corollaire famille libre correspond un neurone de la couche cachée. Tous ont des rôles symétriques les uns par rapport aux autres ce qui ne serait pas le cas si les fonctions de transfert étaient des polynômes. C’est une des raisons pour lesquelles les réseaux de neurones ont du succès. Le théorème densité et le corollaire famille libre sont aussi vraies pour des fonctions du type exponentielle : $\pa{y,b} \in \mathbb{R}^p \times \mathbb{R} \longrightarrow e^{-\pa{<y,x>+b}^2}$ . Maintenant qu’il est prouvé que les réseaux de neurones conviennent pour modéliser $f$ dans l’équation (2), il reste à étudier les méthodes qui permettent de trouver les paramètres $W^*$ optimaux de cette fonction.