ROC#

A few graphs about ROC on the iris datasets.

[1]:

%matplotlib inline
import matplotlib.pyplot as plt

Iris datasets#

[3]:

from sklearn import datasets

iris = datasets.load_iris()
X = iris.data[:, :2]
y = iris.target

[4]:

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33)

[5]:

from sklearn.linear_model import LogisticRegression

clf = LogisticRegression()
clf.fit(X_train, y_train)

[5]:

LogisticRegression(C=1.0, class_weight=None, dual=False, fit_intercept=True,
          intercept_scaling=1, max_iter=100, multi_class='ovr', n_jobs=1,
          penalty='l2', random_state=None, solver='liblinear', tol=0.0001,
          verbose=0, warm_start=False)

[6]:

import numpy

ypred = clf.predict(X_test)
yprob = clf.predict_proba(X_test)
score = numpy.array(list(yprob[i, ypred[i]] for i in range(len(ypred))))

[7]:

data = numpy.zeros((len(ypred), 2))
data[:, 0] = score.ravel()
data[ypred == y_test, 1] = 1
data[:5]

[7]:

array([[ 0.70495209,  1.        ],
       [ 0.56148737,  0.        ],
       [ 0.56148737,  1.        ],
       [ 0.77416227,  1.        ],
       [ 0.58631799,  0.        ]])

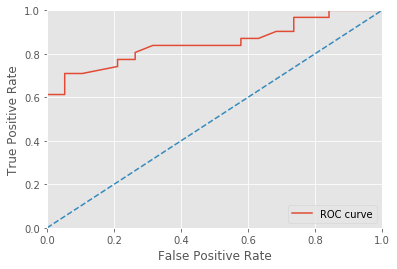
ROC with scikit-learn#

We use the following example Receiver Operating Characteristic (ROC).

[8]:

from sklearn.metrics import roc_curve

fpr, tpr, th = roc_curve(y_test == ypred, score)

[9]:

plt.plot(fpr, tpr, label="ROC curve")
plt.plot([0, 1], [0, 1], linestyle="--")
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.0])
plt.xlabel("False Positive Rate")
plt.ylabel("True Positive Rate")
plt.legend(loc="lower right")

[9]:

<matplotlib.legend.Legend at 0x268373a2128>

../../_images/notebooks_metric_roc_example_10_1.png

[10]:

import pandas

df = pandas.DataFrame(dict(fpr=fpr, tpr=tpr, threshold=th))
df

[10]:

	fpr	threshold	tpr
0	0.000000	0.910712	0.032258
1	0.000000	0.869794	0.096774
2	0.000000	0.863174	0.161290
3	0.000000	0.805864	0.258065
4	0.000000	0.790909	0.387097
5	0.000000	0.650510	0.612903
6	0.052632	0.634499	0.612903
7	0.052632	0.620319	0.709677
8	0.105263	0.615015	0.709677
9	0.210526	0.607975	0.741935
10	0.210526	0.604496	0.774194
11	0.263158	0.586318	0.774194
12	0.263158	0.584172	0.806452
13	0.315789	0.561487	0.838710
14	0.421053	0.556499	0.838710
15	0.578947	0.525449	0.838710
16	0.578947	0.522579	0.870968
17	0.631579	0.522551	0.870968
18	0.684211	0.520835	0.903226
19	0.736842	0.516687	0.903226
20	0.736842	0.453826	0.967742
21	0.842105	0.417941	0.967742
22	0.842105	0.412703	1.000000
23	1.000000	0.375573	1.000000

ROC - TPR / FPR#

We do the same with the class this module provides ROC.

TPR = True Positive Rate
FPR = False Positive Rate

You can see as TPR the distribution function of a score for a positive example and the FPR the same for a negative example.

[11]:

from mlstatpy.ml.roc import ROC

[12]:

roc = ROC(df=data)

[13]:

roc

[13]:

Overall precision: 0.63 - AUC=0.850594
--------------
      score  label  weight
0  0.375573    0.0     1.0
1  0.385480    0.0     1.0
2  0.412314    0.0     1.0
3  0.412703    1.0     1.0
4  0.417941    0.0     1.0
--------------
       score  label  weight
45  0.863174    1.0     1.0
46  0.863174    1.0     1.0
47  0.869794    1.0     1.0
48  0.903335    1.0     1.0
49  0.910712    1.0     1.0
--------------
    False Positive Rate  True Positive Rate  threshold
0              0.000000            0.032258   0.910712
1              0.000000            0.193548   0.828617
2              0.000000            0.354839   0.790909
3              0.000000            0.516129   0.737000
4              0.052632            0.645161   0.627589
5              0.157895            0.741935   0.607975
6              0.263158            0.838710   0.561487
7              0.526316            0.838710   0.542211
8              0.684211            0.903226   0.520835
9              0.842105            0.967742   0.417941
10             1.000000            1.000000   0.375573
--------------
       error  recall  threshold
0   0.000000    0.02   0.910712
1   0.000000    0.12   0.828617
2   0.000000    0.22   0.790909
3   0.000000    0.32   0.737000
4   0.047619    0.42   0.627589
5   0.115385    0.52   0.607975
6   0.161290    0.62   0.561487
7   0.277778    0.72   0.542211
8   0.317073    0.82   0.520835
9   0.347826    0.92   0.417941
10  0.380000    1.00   0.375573

[14]:

roc.auc()

[14]:

0.85059422750424452

[15]:

roc.plot(nb=10)

[15]:

<matplotlib.axes._subplots.AxesSubplot at 0x2683ff2b668>

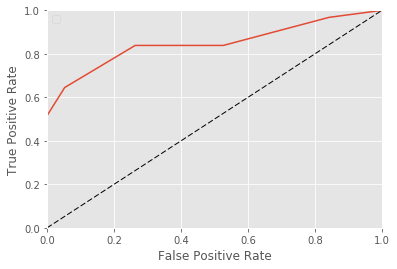
../../_images/notebooks_metric_roc_example_17_1.png

This function draws the curve with only 10 points but we can ask for more.

[16]:

roc.plot(nb=100)

[16]:

<matplotlib.axes._subplots.AxesSubplot at 0x2683feba240>

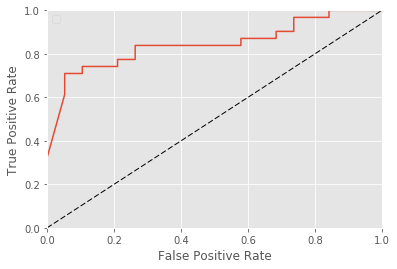
../../_images/notebooks_metric_roc_example_19_1.png

We can also ask to draw bootstropped curves to get a sense of the confidence.

[17]:

roc.plot(nb=10, bootstrap=10)

[17]:

<matplotlib.axes._subplots.AxesSubplot at 0x26840008748>

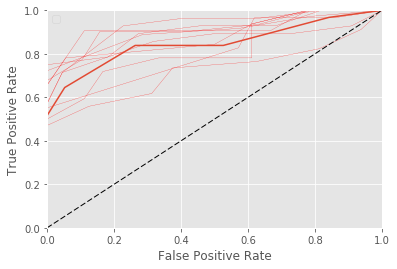
../../_images/notebooks_metric_roc_example_21_1.png

ROC - score distribution#

This another representation for the metrics FPR and TPR. \(P(x<s)\) is the probability that a score for a positive example to be less than \(s\). \(P(->s)\) is the probability that a score for a negative example to be higher than \(s\). We assume in this case that the higher the better for the score.

[18]:

roc.plot(curve=ROC.CurveType.PROBSCORE, thresholds=True)

[18]:

<matplotlib.axes._subplots.AxesSubplot at 0x268410618d0>

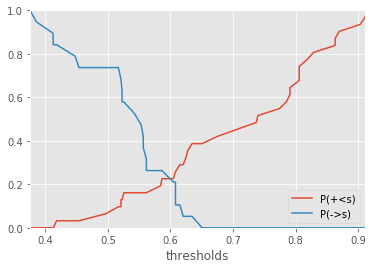
../../_images/notebooks_metric_roc_example_23_1.png

When curves intersects at score \(s^*\), error rates for positive and negative examples are equal. If we show the confusion matrix for this particular score \(s^*\), it gives:

[19]:

conf = roc.confusion()
conf["P(+<s)"] = 1 - conf["True Positive"] / conf.loc[len(conf) - 1, "True Positive"]
conf["P(->s)"] = 1 - conf["True Negative"] / conf.loc[0, "True Negative"]
conf

[19]:

	True Positive	False Positive	False Negative	True Negative	threshold	P(+<s)	P(->s)
0	0.0	0.0	31.0	19.0	0.910712	1.000000	0.000000
1	1.0	0.0	30.0	19.0	0.910712	0.967742	0.000000
2	6.0	0.0	25.0	19.0	0.828617	0.806452	0.000000
3	11.0	0.0	20.0	19.0	0.790909	0.645161	0.000000
4	16.0	0.0	15.0	19.0	0.737000	0.483871	0.000000
5	20.0	1.0	11.0	18.0	0.627589	0.354839	0.052632
6	23.0	3.0	8.0	16.0	0.607975	0.258065	0.157895
7	26.0	5.0	5.0	14.0	0.561487	0.161290	0.263158
8	26.0	10.0	5.0	9.0	0.542211	0.161290	0.526316
9	28.0	13.0	3.0	6.0	0.520835	0.096774	0.684211
10	30.0	16.0	1.0	3.0	0.417941	0.032258	0.842105
11	31.0	19.0	0.0	0.0	0.375573	0.000000	1.000000

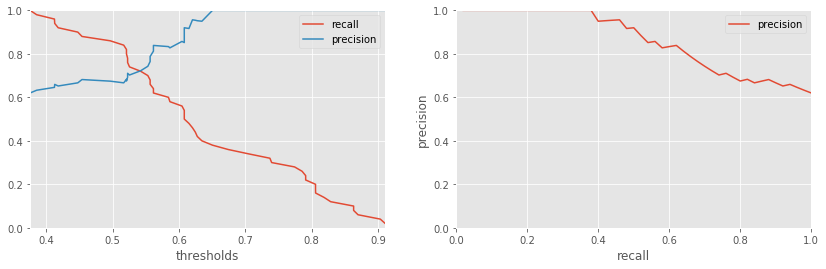
ROC - recall / precision#

In this representation, we show the score.

[20]:

import matplotlib.pyplot as plt

fig, axes = plt.subplots(ncols=2, nrows=1, figsize=(14, 4))
roc.plot(curve=ROC.CurveType.RECPREC, thresholds=True, ax=axes[0])
roc.plot(curve=ROC.CurveType.RECPREC, ax=axes[1])

[20]:

<matplotlib.axes._subplots.AxesSubplot at 0x2684151d3c8>

../../_images/notebooks_metric_roc_example_27_1.png

[21]: