NeuralTreeNet et coût

La classe NeuralTreeNet convertit un arbre de décision en réseau de neurones. Si la conversion n’est pas exacte mais elle permet d’obtenir un modèle différentiable et apprenable avec un algorithme d’optimisation à base de gradient. Ce notebook compare le temps d’éxécution entre un arbre et le réseau de neurones.

%matplotlib inline

Jeux de données

On construit un jeu de données aléatoire.

import numpy

X = numpy.random.randn(10000, 10)
y = X.sum(axis=1) / X.shape[1]
X = X.astype(numpy.float64)
y = y.astype(numpy.float64)

middle = X.shape[0] // 2
X_train, X_test = X[:middle], X[middle:]
y_train, y_test = y[:middle], y[middle:]

Caler un arbre de décision

from sklearn.tree import DecisionTreeRegressor

tree = DecisionTreeRegressor(max_depth=7)
tree.fit(X_train, y_train)
tree.score(X_train, y_train), tree.score(X_test, y_test)

(0.6225001966466359, 0.37938295559354807)

from sklearn.metrics import r2_score

r2_score(y_test, tree.predict(X_test))

0.37938295559354807

Covnersion de l’arbre en réseau de neurones

from pandas import DataFrame
from mlstatpy.ml.neural_tree import NeuralTreeNet, NeuralTreeNetRegressor

xe = X_test.astype(numpy.float32)
expected = tree.predict(xe)

nn = NeuralTreeNetRegressor(NeuralTreeNet.create_from_tree(tree, arch="compact"))
got = nn.predict(xe)
me = numpy.abs(got - expected).mean()
mx = numpy.abs(got - expected).max()
DataFrame([{"average absolute error": me, "max absolute error": mx}]).T

	0
average absolute error	0.208776
max absolute error	1.427806

La conversion est loin d’être parfaite. La raison vient du fait que les fonctions de seuil sont approchées par des fonctions sigmoïdes. Il suffit d’une erreur minime pour que la décision prenne un chemin différent dans l’arbre et soit complètement différente.

Conversion au format ONNX

from skl2onnx import to_onnx

onx_tree = to_onnx(tree, X[:1].astype(numpy.float32))
onx_nn = to_onnx(nn, X[:1].astype(numpy.float32))

Le réseau de neurones peut être représenté comme suit.

from onnx_array_api.plotting.text_plot import onnx_simple_text_plot

print(onnx_simple_text_plot(onx_nn))

opset: domain='' version=21
input: name='X' type=dtype('float32') shape=['', 10]
init: name='Ma_MatMulcst' type=dtype('float32') shape=(10, 127)
init: name='Ad_Addcst' type=dtype('float32') shape=(127,)
init: name='Mu_Mulcst' type=dtype('float32') shape=(1,) -- array([4.], dtype=float32)
init: name='Ma_MatMulcst1' type=dtype('float32') shape=(127, 128)
init: name='Ad_Addcst1' type=dtype('float32') shape=(128,)
init: name='Ma_MatMulcst2' type=dtype('float32') shape=(128, 1)
init: name='Ad_Addcst2' type=dtype('float32') shape=(1,) -- array([0.], dtype=float32)
MatMul(X, Ma_MatMulcst) -> Ma_Y02
  Add(Ma_Y02, Ad_Addcst) -> Ad_C02
    Mul(Ad_C02, Mu_Mulcst) -> Mu_C01
      Sigmoid(Mu_C01) -> Si_Y01
        MatMul(Si_Y01, Ma_MatMulcst1) -> Ma_Y01
          Add(Ma_Y01, Ad_Addcst1) -> Ad_C01
            Mul(Ad_C01, Mu_Mulcst) -> Mu_C0
              Sigmoid(Mu_C0) -> Si_Y0
                MatMul(Si_Y0, Ma_MatMulcst2) -> Ma_Y0
                  Add(Ma_Y0, Ad_Addcst2) -> Ad_C0
                    Identity(Ad_C0) -> variable
output: name='variable' type=dtype('float32') shape=['', 1]

Temps de calcul des prédictions

from onnxruntime import InferenceSession

oinf_tree = InferenceSession(onx_tree.SerializeToString())
oinf_nn = InferenceSession(onx_nn.SerializeToString())

%timeit tree.predict(xe)

584 μs ± 16.3 μs per loop (mean ± std. dev. of 7 runs, 1,000 loops each)

%timeit oinf_tree.run(None, {'X': xe})

48.4 μs ± 1.16 μs per loop (mean ± std. dev. of 7 runs, 10,000 loops each)

%timeit oinf_nn.run(None, {'X': xe})

1.28 ms ± 97.7 μs per loop (mean ± std. dev. of 7 runs, 1,000 loops each)

Le temps de calcul est nettement plus long pour le réseau de neurones. Si l’arbre de décision a une profondeur de d, l’arbre de décision va faire exactement d comparaisons. Le réseau de neurones quant à lui évalue tous les seuils pour chaque prédiction, soit \(2^d\). Vérifions cela en faisant variable la profondeur.

Temps de calcul en fonction de la profondeur

from tqdm import tqdm
from onnx_array_api.ext_test_case import measure_time

data = []
for d in tqdm(range(2, 10)):
    tree = DecisionTreeRegressor(max_depth=d)
    tree.fit(X_train, y_train)
    obs = measure_time(lambda tree=tree: tree.predict(xe), number=20, repeat=20)
    obs.update(dict(d=d, exp="skl"))
    data.append(obs)

    nn = NeuralTreeNetRegressor(NeuralTreeNet.create_from_tree(tree, arch="compact"))

    onx_tree = to_onnx(tree, X[:1].astype(numpy.float32))
    onx_nn = to_onnx(nn, X[:1].astype(numpy.float32))
    oinf_tree = InferenceSession(
        onx_tree.SerializePartialToString(), providers=["CPUExecutionProvider"]
    )
    oinf_nn = InferenceSession(
        onx_nn.SerializePartialToString(), providers=["CPUExecutionProvider"]
    )

    obs = measure_time(
        lambda oinf_tree=oinf_tree: oinf_tree.run(None, {"X": xe}), number=10, repeat=10
    )
    obs.update(dict(d=d, exp="onx_tree"))
    data.append(obs)

    obs = measure_time(
        lambda oinf_nn=oinf_nn: oinf_nn.run(None, {"X": xe}), number=10, repeat=10
    )
    obs.update(dict(d=d, exp="onx_nn"))
    data.append(obs)

df = DataFrame(data)
df

100%|██████████| 8/8 [00:04<00:00,  1.63it/s]

	average	deviation	min_exec	max_exec	repeat	number	ttime	context_size	d	exp
0	0.000207	0.000045	0.000153	0.000317	20	20	0.004147	64	2	skl
1	0.000151	0.000246	0.000031	0.000825	10	10	0.001515	64	2	onx_tree
2	0.000178	0.000093	0.000119	0.000371	10	10	0.001781	64	2	onx_nn
3	0.000249	0.000036	0.000220	0.000360	20	20	0.004980	64	3	skl
4	0.000312	0.000156	0.000113	0.000661	10	10	0.003117	64	3	onx_tree
5	0.000352	0.000204	0.000182	0.000831	10	10	0.003523	64	3	onx_nn
6	0.000339	0.000073	0.000257	0.000487	20	20	0.006775	64	4	skl
7	0.000337	0.000423	0.000059	0.001537	10	10	0.003368	64	4	onx_tree
8	0.000619	0.000354	0.000221	0.001320	10	10	0.006194	64	4	onx_nn
9	0.000359	0.000038	0.000309	0.000453	20	20	0.007171	64	5	skl
10	0.000473	0.000565	0.000064	0.001923	10	10	0.004729	64	5	onx_tree
11	0.001197	0.000944	0.000309	0.003529	10	10	0.011973	64	5	onx_nn
12	0.000386	0.000022	0.000359	0.000439	20	20	0.007715	64	6	skl
13	0.000793	0.000770	0.000097	0.002445	10	10	0.007926	64	6	onx_tree
14	0.001521	0.000919	0.000652	0.003820	10	10	0.015207	64	6	onx_nn
15	0.000429	0.000024	0.000404	0.000494	20	20	0.008579	64	7	skl
16	0.000658	0.000662	0.000207	0.002484	10	10	0.006575	64	7	onx_tree
17	0.002925	0.002770	0.001489	0.011048	10	10	0.029251	64	7	onx_nn
18	0.000508	0.000059	0.000452	0.000733	20	20	0.010157	64	8	skl
19	0.001235	0.001208	0.000121	0.003842	10	10	0.012347	64	8	onx_tree
20	0.004627	0.004239	0.002962	0.017300	10	10	0.046271	64	8	onx_nn
21	0.000558	0.000045	0.000498	0.000700	20	20	0.011152	64	9	skl
22	0.000745	0.000540	0.000138	0.002166	10	10	0.007449	64	9	onx_tree
23	0.011127	0.004856	0.009014	0.025667	10	10	0.111265	64	9	onx_nn

piv = df.pivot(index="d", columns="exp", values="average")
piv.plot(logy=True, title="Temps de calcul en fonction de la profondeur");

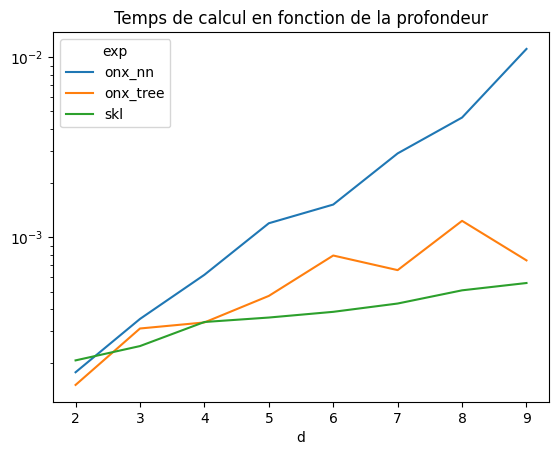
L’hypothèse est vérifiée.