Carte de Kohonen

Principe

Les cartes de Kohonen ou Self Organizing Map (SOM) est le terme anglais pour les cartes de Kohonen. (voir [Kohonen1997]) sont assimilées à des méthodes neuronales. Ces cartes sont constituées d’un ensemble de neurones \(\vecteur{\mu_1}{\mu_N}\) lesquels sont reliés par une forme récurrente de voisinage. Les neurones sont initialement répartis selon ce système de voisinage. Le réseau évolue ensuite puisque chaque point de l’espace parmi l’ensemble \(\vecteur{X_1}{X_K}\) attire le neurone le plus proche vers lui, ce neurone attirant à son tour ses voisins. Cette procédure est réitérée jusqu’à convergence du réseau en faisant décroître l’attirance des neurones vers les points du nuage.

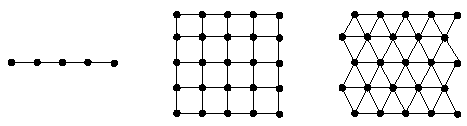
Trois types de voisinages couramment utilisés pour les cartes de Kohonen, voisinages linéaire, rectangulaire, triangulaire.

Algorithme A1 : cartes de Kohonen (SOM)

Soient \(\vecteur{\mu_1^t}{\mu_N^t} \in \pa{\mathbb{R}^n}^N\) des neurones de l’espace vectoriel \(\mathbb{R}^n\). On désigne par \(V\pa{\mu_j}\) l’ensemble des neurones voisins de \(\mu_j\) pour cette carte de Kohonen. Par définition, on a \(\mu_j \in V\pa{\mu_j}\). Soit \(\vecteur{X_1}{X_K} \in \pa{\mathbb{R}^n}^K\) un nuage de points. On utilise une suite de réels positifs \(\pa{\alpha_t}\) vérifiant \(\sum_{t \supegal 0} \alpha_t^2 < \infty\) et \(\sum_{t \supegal 0} \alpha_t = \infty\).

initialisation

Les neurones \(\vecteur{\mu_1^0}{\mu_N^0}\) sont répartis dans l’espace \(\mathbb{R}^n\) de manière régulière selon la forme de leur voisinage. \(t \longleftarrow 0\).

neurone le plus proche

On choisi aléatoirement un points du nuage \(X_i\) puis on définit le neurone \(\mu_{k^*}^t\) de telle sorte que : \(\norme{ \mu_{k^*}^t - X_i} = \underset{1 \infegal j \infegal N}{\min } \; \norme{ \mu_j^t - X_i }\).

mise à jour

foreach \(\mu^t_j\) in \(V\pa{\mu_{k^*}^t}\)

\(\mu^{t+1}_j \longleftarrow \mu^t_j + \alpha_t \, \pa{X_i - \mu^{t+1}_j}\)

\(t \longleftarrow t + 1\)

Tant que l’algorithme n’a pas convergé, retour à l’étape du neurone le plus proche.

L’étape de mise à jour peut être modifiée de manière à améliorer la vitesse de convergence (voir [Lo1991]) :

\[\mu^{t+1}_j \longleftarrow \mu^t_j + \alpha_t \, h\pa{\mu^{t}_j, \mu_{k^*}^t} \, \mu_k\pa{X_i - \mu^{t+1}_j}\]

Où \(h\) est une fonction à valeur dans l’intervalle \(\cro{0,1}\) qui vaut 1 lorsque \(\mu^t_j = \mu_{k^*}^t\) et qui décroît lorsque la distance entre ces deux neurones augmente. Une fonction typique est : \(h\pa{x,y} = h_0 \, \exp\pa{ - \frac{\norme{x-y}^2} {2\, \sigma_t^2} }\).

Les cartes de Kohonen sont utilisées en analyse des données afin de projeter un nuage de points dans un espace à deux dimensions d’une manière non linéaire en utilisant un voisinage rectangulaire. Elles permettent également d’effectuer une classification non supervisée en regroupant les neurones là où les points sont concentrés. Les arêtes reliant les neurones ou sommets de la cartes de Kohonen sont soit rétrécies pour signifier que deux neurones sont voisins, soit distendues pour indiquer une séparation entre classes.

Carte de Kohonen et classification

L’article [Wu2004] aborde le problème d’une classification à partir du résultat obtenu depuis une carte de Kohonen. Plutôt que de classer les points, ce sont les neurones qui seront classés en \(C\) classes. Après avoir appliqué l”algorithme de Kohonen, la méthode proposée dans [Wu2004] consiste à classer de manière non supervisée les \(A\) neurones obtenus \(\vecteur{\mu_1}{\mu_A}\). Toutefois, ceux-ci ne sont pas tous pris en compte afin d’éviter les points aberrants. On suppose que \(\alpha_{il} = 1\) si le neurone \(l\) est le plus proche du point \(X_i\), 0 dans le cas contraire. Puis on construit les quantités suivantes :

\begin{eqnarray*} \nu_k &=& \sum_{i=1}^{N} \; \alpha_{ik} \\ T_k &=& \frac{1}{\nu_k} \; \sum_{i=1}^{N} \; \alpha_{ik} X_i \\ \theta(T_k) &=& \sqrt{ \frac{1}{\nu_k} \; \sum_{i=1}^{N} \; \alpha_{ik} \norme{ X_i - T_k}^2 } \end{eqnarray*}

De plus :

\begin{eqnarray*} \overline{\theta} &=& \frac{1}{A} \; \sum_{k=1}^{A} \theta(T_k) \\ \sigma(\theta) &=& \sqrt{ \frac{1}{A} \; \sum_{k=1}^{A} \pa{ \theta(T_k) - \overline{\theta} }^2 } \end{eqnarray*}

Si \(\nu_k = 0\) ou \(\norme{ \mu_k - T_k} > \overline{\theta} + \sigma(\theta)\), le neurone \(\mu_k\) n’est pas prise en compte lors de la classification non supervisée. Une fois celle-ci terminée, chaque élément \(X_i\) est classé selon la classe du neurone le plus proche.

L’article [Wu2004] propose également un critère permettant de déterminer le nombre de classes idéale. On note, \(a_{ik} = 1\) si \(X_i\) appartient à la classe \(k\), dans le cas contraire, \(a_{ik} = 0\). On définit \(n_k\) le nombre d’éléments de la classe \(k\), le vecteur moyenne \(M_k\) associé à la classe \(k\) :

\begin{eqnarray*} n_k &=& \sum_{i=1}^{N} \; a_{ik} \\ M_k &=& \frac{1}{n_k} \; \sum_{i=1}^{N} \; a_{ik} X_i \\ \sigma^2(M_k) &=& \frac{1}{n_k} \; \sum_{i=1}^{N} \; a_{ik} \norme{ X_i - M_k}^2 \end{eqnarray*}

On note au préalable \(\sigma = \sqrt{ \frac{1}{C} \sum_{k=1}^{C} \; \sigma^2(M_k) }\). L’article définit ensuite la densité interne pour \(C\) classes :

\begin{eqnarray*} D_{int} (C) &=& \frac{1}{C} \; \sum_{k=1}^{C} \; \sum_{i=1}^{N} \; \sum_{j=1}^{N} \; a_{ik} a_{jk} \indicatrice{ \norme{ X_i - X_j} \infegal \sigma } \end{eqnarray*}

On définit la distance \(d^*_{kl}\) pour \(\pa{k,l} \in \ensemble{1}{C}^2\), cette distance est égale à la distance minimale pour un couple de points, le premier appartenant à la classe \(i\), le second à la classe \(j\) :

\begin{eqnarray*} d^*_{kl} &=& \min \acc{ \norme{ X_i - X_j} \sac a_{ik} a_{jl} = 1 } = \norme{ X_{i^*}^{kl} - X_{j^*}^{kl} } \end{eqnarray*}

La densité externe est alors définie en fonction du nombre de classes \(C\) par :

\begin{eqnarray*} D_{ext} (C) = \sum_{k=1}^{C} \; \sum_{l=1}^{C} \; \cro{ \frac{ d_{kl} } { \sigma\pa{k} \sigma\pa{l} } \; \sum_{i=1}^{N} \; \indicatrice{ a_{ik} + a_{il} > 0 } \indicatrice{ \norme{ X_i - \frac{X_{i^*}^{kl} + X_{j^*}^{kl}}{2} } \infegal \frac{\sigma\pa{k} +\sigma\pa{l}}{2} } } \end{eqnarray*}

L’article définit ensuite la séparabilité en fonction du nombre de classes \(C\) :

\[Sep(C) = \frac{1}{D_{ext}(C)} \; \sum_{k=1}^{C} \; \sum_{l=1}^{C} \; d^*_{kl}\]

Enfin, le critère Composing Density Between and With clusters noté \(CDBw(C)\) est défini par :

\[CDBw(C) = D_{int} (C) * Sep(C)\]

Ce critère est maximal pour un nombre de classes optimal. Outre les résultats de l’article [Wu2004] sommairement résumés ici, ce dernier revient sur l’histoire des cartes de Kohonen, depuis leur création [Kohonen1982] jusqu’aux derniers développements récents.

Autres utilisation des cartes de Kohenen

On peut les utiliser pour déterminer le plus court chemin passant par tous les noeuds d’un graphe, c’est à dire appliquer Kohonen au problème du voyageur de commerce.

Bibliographie

[Kohonen1982]

Self-organized formation of topologically correct feature maps (1982), T. Kohonen, Biol. Cybern., volume (43), pages 59-69

[Kohonen1997]

Self-Organizing Map (1997) T. Kohonen, Springer

[Lo1991]

On the rate of convergence in topology preserving neural networks (1991), Z. Lo, B. Bavarian, Biological Cybernetics, volume 63, pages 55-63

[Wu2004] (1,2,3,4)

Clustering of the self-organizing map using a clustering validity index based on inter-cluster and intra-cluster density (2004), Sitao Wu, Tommy W. S. Chow, Pattern Recognition, volume (37), pages 175-188