Valeurs manquantes et factorisation de matrices¶
Réflexion autour des valeur manquantes et de la factorisation de matrice positive.
[2]:
%matplotlib inline
Matrice à coefficients aléatoires¶
On étudie la factorisation d’une matrice à coefficients tout à fait aléatoires qui suivent une loi uniforme sur l’intervalle . Essayons sur une petite matrice :
[3]:
from numpy.random import rand
M = rand(3, 3)
M
[3]:
array([[ 0.05119593, 0.43722929, 0.9290821 ],
[ 0.4588466 , 0.14187813, 0.23762633],
[ 0.9768084 , 0.47674026, 0.79044526]])
[4]:
from sklearn.decomposition import NMF
mf = NMF(1)
mf.fit_transform(M)
[4]:
array([[ 0.67825803],
[ 0.38030919],
[ 1.02295362]])
La matrice précédente est la matrice dans le produit
, la matrice qui suit est
.
[5]:
mf.components_
[5]:
array([[ 0.73190904, 0.50765757, 0.92611883]])
[6]:
mf.reconstruction_err_ / (M.shape[0] * M.shape[1])
[6]:
0.07236890712696428
On recalcule l’erreur :
[7]:
d = M - mf.fit_transform(M) @ mf.components_
a = d.ravel()
e = a @ a.T
e**0.5 / (M.shape[0] * M.shape[1])
[7]:
0.072368907126964283
[8]:
e.ravel()
[8]:
array([ 0.42421796])
Et maintenant sur une grande et plus nécessairement carrée :
[9]:
M = rand(300, 10)
mf = NMF(1)
mf.fit_transform(M)
mf.reconstruction_err_ / (M.shape[0] * M.shape[1])
[9]:
0.004996164872801101
L’erreur est la même :
[10]:
errs = []
rangs = list(range(1, 11))
for k in rangs:
mf = NMF(k)
mf.fit_transform(M)
e = mf.reconstruction_err_ / (M.shape[0] * M.shape[1])
errs.append(e)
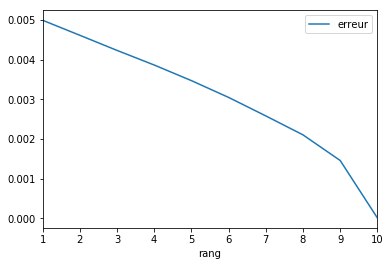
[11]:
import pandas
df = pandas.DataFrame(dict(rang=rangs, erreur=errs))
df.plot(x="rang", y="erreur")
[11]:
<matplotlib.axes._subplots.AxesSubplot at 0x199924d8668>
Matrice avec des vecteurs colonnes corrélés¶
Supposons maintenant que la matrice précédente est de rang 3. Pour s’en assurer, on tire une matrice aléalatoire avec 3 vecteurs colonnes et on réplique des colonnes jusqu’à la dimension souhaitée.
[12]:
from numpy import hstack
M = rand(300, 3)
M = hstack([M, M, M, M[:, :1]])
M.shape
[12]:
(300, 10)
[13]:
errs = []
rangs = list(range(1, 11))
for k in rangs:
mf = NMF(k)
mf.fit_transform(M)
e = mf.reconstruction_err_ / (M.shape[0] * M.shape[1])
errs.append(e)
[14]:
import pandas
df = pandas.DataFrame(dict(rang=rangs, erreur=errs))
df.plot(x="rang", y="erreur")
[14]:
<matplotlib.axes._subplots.AxesSubplot at 0x199925d6630>
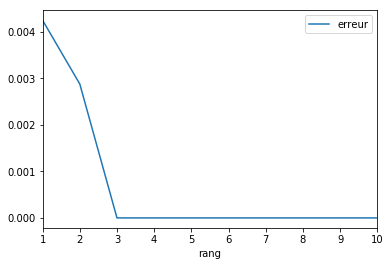
On essaye à nouveausur une matrice un peu plus petite.
[15]:
M = rand(3, 2)
M = hstack([M, M[:, :1]])
M
[15]:
array([[ 0.27190312, 0.6497563 , 0.27190312],
[ 0.44853292, 0.87097224, 0.44853292],
[ 0.29424835, 0.65106952, 0.29424835]])
[16]:
mf = NMF(2)
mf.fit_transform(M)
[16]:
array([[ 0.61835197, 0. ],
[ 0.82887888, 0.29866219],
[ 0.61960446, 0.07743224]])
[17]:
mf.components_
[17]:
array([[ 0.43972536, 1.05078419, 0.43972536],
[ 0.28143493, 0. , 0.28143493]])
La dernière colonne est identique à la première.
Matrice identité¶
Et maintenant si la matrice est la matrice identité, que se passe-t-il ?
[18]:
from numpy import identity
M = identity(3)
M
[18]:
array([[ 1., 0., 0.],
[ 0., 1., 0.],
[ 0., 0., 1.]])
[19]:
mf = NMF(1)
mf.fit_transform(M)
[19]:
array([[ 0.],
[ 1.],
[ 0.]])
[20]:
mf.components_
[20]:
array([[ 0., 1., 0.]])
[21]:
mf.reconstruction_err_**2
[21]:
2.0000000000000004
On essaye avec .
[22]:
mf = NMF(2)
mf.fit_transform(M)
[22]:
array([[ 0. , 0. ],
[ 0. , 1.03940448],
[ 0.95521772, 0. ]])
[23]:
mf.components_
[23]:
array([[ 0. , 0. , 1.04688175],
[ 0. , 0.96208937, 0. ]])
[24]:
mf.reconstruction_err_**2
[24]:
1.0
Avec des vecteurs normés et indépendants (formant donc une base de l’espace vectoriel), l’algorithme aboutit à une matrice égale au
premiers vecteurs et oublie les autres.
Matrice identité et représentation spatiale¶
Pour comprendre un peu mieux ce dernier exemple, il est utile de chercher d’autres solutions dont l’erreur est équivalente.
[25]:
def erreur_mf(M, W, H):
d = M - W @ H
a = d.ravel()
e = a @ a.T
e**0.5 / (M.shape[0] * M.shape[1])
return e
M = identity(3)
mf = NMF(2)
W = mf.fit_transform(M)
H = mf.components_
erreur_mf(M, W, H)
[25]:
1.0
[26]:
W
[26]:
array([[ 0. , 0. ],
[ 0.9703523 , 0. ],
[ 0. , 1.02721047]])
[27]:
H
[27]:
array([[ 0. , 1.03055354, 0. ],
[ 0. , 0. , 0.97351032]])
[28]:
W @ H
[28]:
array([[ 0., 0., 0.],
[ 0., 1., 0.],
[ 0., 0., 1.]])
[29]:
import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.add_subplot(111, projection="3d")
wh = W @ H
ax.scatter(M[:, 0], M[:, 1], M[:, 2], c="b", marker="o", s=20)
ax.scatter(wh[:, 0], wh[:, 1], wh[:, 2], c="r", marker="^")
[29]:
<mpl_toolkits.mplot3d.art3d.Path3DCollection at 0x19992d2a5c0>
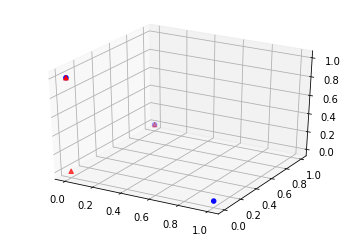
Et si on pose maintenant :
[30]:
import numpy
W = numpy.array([[0.5, 0.5, 0], [0, 0, 1]]).T
H = numpy.array([[1, 1, 0], [0.0, 0.0, 1.0]])
W
[30]:
array([[ 0.5, 0. ],
[ 0.5, 0. ],
[ 0. , 1. ]])
[31]:
H
[31]:
array([[ 1., 1., 0.],
[ 0., 0., 1.]])
[32]:
W @ H
[32]:
array([[ 0.5, 0.5, 0. ],
[ 0.5, 0.5, 0. ],
[ 0. , 0. , 1. ]])
[33]:
erreur_mf(M, W, H)
[33]:
1.0
[34]:
fig = plt.figure()
ax = fig.add_subplot(111, projection="3d")
wh = W @ H
ax.scatter(M[:, 0], M[:, 1], M[:, 2], c="b", marker="o", s=20)
ax.scatter(wh[:, 0], wh[:, 1], wh[:, 2], c="r", marker="^")
[34]:
<mpl_toolkits.mplot3d.art3d.Path3DCollection at 0x19992a2e5f8>
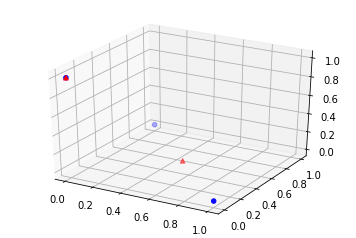
On peut voir la matrice comme un ensemble de
points dans un espace vectoriel. La matrice
est un ensemble de
points dans le même espace. La matrice
, de rang
est une approximation de cet ensemble dans le même espace, c’est aussi
combinaisons linéaires de
points de façon à former
points les plus proches proches de
points de la matrice
.
[35]: