101: Linear Regression and export to ONNX¶

scikit-learn and torch to train a linear regression.

data¶

import numpy as np
from sklearn.datasets import make_regression
from sklearn.linear_model import LinearRegression, SGDRegressor
from sklearn.metrics import mean_squared_error, r2_score
from sklearn.model_selection import train_test_split
import torch
from onnxruntime import InferenceSession
from experimental_experiment.helpers import pretty_onnx
from onnx_array_api.plotting.graphviz_helper import plot_dot
from experimental_experiment.torch_interpreter import to_onnx


X, y = make_regression(1000, n_features=5, noise=10.0, n_informative=2)
print(X.shape, y.shape)

X_train, X_test, y_train, y_test = train_test_split(X, y)

(1000, 5) (1000,)

scikit-learn: the simple regression¶

$A^* = (X'X)^{-1}X'Y$

clr = LinearRegression()
clr.fit(X_train, y_train)

print(f"coefficients: {clr.coef_}, {clr.intercept_}")

coefficients: [-0.5905277  68.17093369 -0.36025951 96.68301034  0.3027038 ], -0.2780205313732105

Evaluation¶

y_pred = clr.predict(X_test)
l2 = mean_squared_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
print(f"LinearRegression: l2={l2}, r2={r2}")

LinearRegression: l2=105.4312962196268, r2=0.9928731076910735

scikit-learn: SGD algorithm¶

SGD = Stochastic Gradient Descent

clr = SGDRegressor(max_iter=5, verbose=1)
clr.fit(X_train, y_train)

print(f"coefficients: {clr.coef_}, {clr.intercept_}")

-- Epoch 1
Norm: 100.67, NNZs: 5, Bias: -1.015924, T: 750, Avg. loss: 1381.368392
Total training time: 0.00 seconds.
-- Epoch 2
Norm: 113.45, NNZs: 5, Bias: -0.702121, T: 1500, Avg. loss: 104.671518
Total training time: 0.00 seconds.
-- Epoch 3
Norm: 116.73, NNZs: 5, Bias: -0.594053, T: 2250, Avg. loss: 55.192374
Total training time: 0.00 seconds.
-- Epoch 4
Norm: 117.79, NNZs: 5, Bias: -0.422715, T: 3000, Avg. loss: 50.917182
Total training time: 0.00 seconds.
-- Epoch 5
Norm: 118.12, NNZs: 5, Bias: -0.303440, T: 3750, Avg. loss: 50.414030
Total training time: 0.00 seconds.
~/vv/this312/lib/python3.12/site-packages/sklearn/linear_model/_stochastic_gradient.py:1579: ConvergenceWarning: Maximum number of iteration reached before convergence. Consider increasing max_iter to improve the fit.
  warnings.warn(
coefficients: [-0.71390393 68.13033061 -0.55820461 96.49022748  0.36404719], [-0.30343975]

Evaluation

y_pred = clr.predict(X_test)
sl2 = mean_squared_error(y_test, y_pred)
sr2 = r2_score(y_test, y_pred)
print(f"SGDRegressor: sl2={sl2}, sr2={sr2}")

SGDRegressor: sl2=105.90326646876946, sr2=0.992841203680981

Linrar Regression with pytorch¶

class TorchLinearRegression(torch.nn.Module):
    def __init__(self, n_dims: int, n_targets: int):
        super().__init__()
        self.linear = torch.nn.Linear(n_dims, n_targets)

    def forward(self, x):
        return self.linear(x)


def train_loop(dataloader, model, loss_fn, optimizer):
    total_loss = 0.0

    # Set the model to training mode - important for batch normalization and dropout layers
    # Unnecessary in this situation but added for best practices
    model.train()
    for X, y in dataloader:
        # Compute prediction and loss
        pred = model(X)
        loss = loss_fn(pred.ravel(), y)

        # Backpropagation
        loss.backward()
        optimizer.step()
        optimizer.zero_grad()

        # training loss
        total_loss += loss

    return total_loss


model = TorchLinearRegression(X_train.shape[1], 1)
optimizer = torch.optim.SGD(model.parameters(), lr=1e-3)
loss_fn = torch.nn.MSELoss()

device = "cpu"
model = model.to(device)
dataset = torch.utils.data.TensorDataset(
    torch.Tensor(X_train).to(device), torch.Tensor(y_train).to(device)
)
dataloader = torch.utils.data.DataLoader(dataset, batch_size=1)


for i in range(5):
    loss = train_loop(dataloader, model, loss_fn, optimizer)
    print(f"iteration {i}, loss={loss}")

iteration 0, loss=3433418.5
iteration 1, loss=256191.859375
iteration 2, loss=85907.140625
iteration 3, loss=76388.796875
iteration 4, loss=75861.7265625

Let’s check the error

y_pred = model(torch.Tensor(X_test)).detach().numpy()
tl2 = mean_squared_error(y_test, y_pred)
tr2 = r2_score(y_test, y_pred)
print(f"TorchLinearRegression: tl2={tl2}, tr2={tr2}")

TorchLinearRegression: tl2=105.14858362218403, tr2=0.9928922183565837

And the coefficients.

print("coefficients:")
for p in model.parameters():
    print(p)

coefficients:
Parameter containing:
tensor([[-0.5513, 68.0744, -0.3509, 96.6450,  0.1641]], requires_grad=True)
Parameter containing:
tensor([-0.3467], requires_grad=True)

Conversion to ONNX¶

Let’s convert it to ONNX.

onx = to_onnx(model, (torch.Tensor(X_test[:2]),), input_names=["x"])

Let’s check it is work.

sess = InferenceSession(onx.SerializeToString(), providers=["CPUExecutionProvider"])
res = sess.run(None, {"x": X_test.astype(np.float32)[:2]})
print(res)

[array([[ 78.82207 ],
       [114.370514]], dtype=float32)]

And the model.

plot_dot(onx)

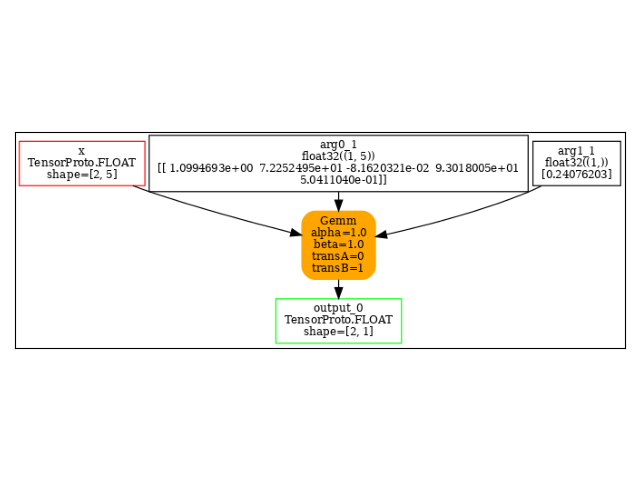
With dynamic shapes¶

The dynamic shapes are used by torch.export.export() and must follow the convention described there. The dynamic dimension allows any value. The model is then valid for many different shapes. That’s usually what users need.

onx = to_onnx(
    model,
    (torch.Tensor(X_test[:2]),),
    input_names=["x"],
    dynamic_shapes={"x": {0: torch.export.Dim("batch")}},
)

print(pretty_onnx(onx))

opset: domain='' version=18
input: name='x' type=dtype('float32') shape=['batch', 5]
init: name='GemmTransposePattern--p_linear_weight::T10' type=float32 shape=(1, 5)-- GraphBuilder.constant_folding.from/fold(init7_s2_1_-1,p_linear_weight::T10)##p_linear_weight::T10/GraphBuilder.constant_folding.from/fold(p_linear_weight)##p_linear_weight/DynamoInterpret.placeholder.1/P(linear.weight)##init7_s2_1_-1/TransposeEqualReshapePattern.apply.new_shape
init: name='linear.bias' type=float32 shape=(1,) -- array([-0.34666494], dtype=float32)-- DynamoInterpret.placeholder.1/P(linear.bias)
Gemm(x, GemmTransposePattern--p_linear_weight::T10, linear.bias, transB=1) -> output_0
output: name='output_0' type=dtype('float32') shape=['batch', 1]

For simplicity, it is possible to use torch.export.Dim.DYNAMIC or torch.export.Dim.AUTO.

onx = to_onnx(
    model,
    (torch.Tensor(X_test[:2]),),
    input_names=["x"],
    dynamic_shapes={"x": {0: torch.export.Dim.DYNAMIC}},
)

print(pretty_onnx(onx))

opset: domain='' version=18
input: name='x' type=dtype('float32') shape=['batch', 5]
init: name='GemmTransposePattern--p_linear_weight::T10' type=float32 shape=(1, 5)-- GraphBuilder.constant_folding.from/fold(init7_s2_1_-1,p_linear_weight::T10)##p_linear_weight::T10/GraphBuilder.constant_folding.from/fold(p_linear_weight)##p_linear_weight/DynamoInterpret.placeholder.1/P(linear.weight)##init7_s2_1_-1/TransposeEqualReshapePattern.apply.new_shape
init: name='linear.bias' type=float32 shape=(1,) -- array([-0.34666494], dtype=float32)-- DynamoInterpret.placeholder.1/P(linear.bias)
Gemm(x, GemmTransposePattern--p_linear_weight::T10, linear.bias, transB=1) -> output_0
output: name='output_0' type=dtype('float32') shape=['batch', 1]

Total running time of the script: (0 minutes 3.357 seconds)