Note
Go to the end to download the full example code.
to_onnx and infer dynamic shapes¶
We try to make it easier to export with dynamic shapes. To do that, we run the model at least twice with a different set of inputs and we try to guess the dynamic shapes found along the way.
Infer dynamic shapes¶
import onnx
from onnx_array_api.plotting.graphviz_helper import plot_dot
import torch
from experimental_experiment.torch_interpreter import to_onnx
from experimental_experiment.torch_interpreter.piece_by_piece import (
trace_execution_piece_by_piece,
)
class MA(torch.nn.Module):
def forward(self, x, y):
return x + y
class MM(torch.nn.Module):
def forward(self, x, y):
return x * y
class MASMM(torch.nn.Module):
def __init__(self):
super().__init__()
self.ma = MA()
self.mm = MM()
def forward(self, x, y, z):
return self.ma(x, y) - self.mm(y, z)
class Model(torch.nn.Module):
def __init__(self):
super().__init__()
self.ma = MA()
self.masmm = MASMM()
def forward(self, x):
return self.ma(x, self.masmm(x, x, x))
The model.
model = Model()
Two sets of inputs.
inputs = [
((torch.randn((5, 6)),), {}),
((torch.randn((6, 6)),), {}),
]
Then we run the model, stores intermediates inputs and outputs, to finally guess the dynamic shapes.
>>> __main__: Model
DS=(({0: <_DimHint.DYNAMIC: 3>},), {})
> ((CT1s5x6[-1.6182637214660645,1.6834182739257812:A0.015691348103185496],),{})
> ((CT1s6x6[-2.494434356689453,3.3988378047943115:A-0.1790965578208367],),{})
>>> ma: MA
DS=(({0: <_DimHint.DYNAMIC: 3>}, {0: <_DimHint.DYNAMIC: 3>}), {})
> ((CT1s5x6[-1.6182637214660645,1.6834182739257812:A0.015691348103185496],CT1s5x6[-5.855304718017578,0.9999058246612549:A-0.7025150872766972]),{})
> ((CT1s6x6[-2.494434356689453,3.3988378047943115:A-0.1790965578208367],CT1s6x6[-11.211071014404297,0.9910044074058533:A-1.6185989735854998]),{})
< (CT1s5x6[-7.473568439483643,2.216357707977295:A-0.68682375450929],)
< (CT1s6x6[-13.70550537109375,2.2497808933258057:A-1.797695554792881],)
<<<
>>> masmm: MASMM
DS=(({0: <_DimHint.DYNAMIC: 3>}, {0: <_DimHint.DYNAMIC: 3>}, {0: <_DimHint.DYNAMIC: 3>}), {})
> ((CT1s5x6[-1.6182637214660645,1.6834182739257812:A0.015691348103185496],CT1s5x6[-1.6182637214660645,1.6834182739257812:A0.015691348103185496],CT1s5x6[-1.6182637214660645,1.6834182739257812:A0.015691348103185496]),{})
> ((CT1s6x6[-2.494434356689453,3.3988378047943115:A-0.1790965578208367],CT1s6x6[-2.494434356689453,3.3988378047943115:A-0.1790965578208367],CT1s6x6[-2.494434356689453,3.3988378047943115:A-0.1790965578208367]),{})
>>> ma: MA
DS=(({0: <_DimHint.DYNAMIC: 3>}, {0: <_DimHint.DYNAMIC: 3>}), {})
> ((CT1s5x6[-1.6182637214660645,1.6834182739257812:A0.015691348103185496],CT1s5x6[-1.6182637214660645,1.6834182739257812:A0.015691348103185496]),{})
> ((CT1s6x6[-2.494434356689453,3.3988378047943115:A-0.1790965578208367],CT1s6x6[-2.494434356689453,3.3988378047943115:A-0.1790965578208367]),{})
< (CT1s5x6[-3.236527442932129,3.3668365478515625:A0.03138269620637099],)
< (CT1s6x6[-4.988868713378906,6.797675609588623:A-0.3581931156416734],)
<<<
>>> mm: MM
DS=(({0: <_DimHint.DYNAMIC: 3>}, {0: <_DimHint.DYNAMIC: 3>}), {})
> ((CT1s5x6[-1.6182637214660645,1.6834182739257812:A0.015691348103185496],CT1s5x6[-1.6182637214660645,1.6834182739257812:A0.015691348103185496]),{})
> ((CT1s6x6[-2.494434356689453,3.3988378047943115:A-0.1790965578208367],CT1s6x6[-2.494434356689453,3.3988378047943115:A-0.1790965578208367]),{})
< (CT1s5x6[0.0006233706953935325,2.833897113800049:A0.7338977855455596],)
< (CT1s6x6[0.0059312377125024796,11.552098274230957:A1.2604058814597212],)
<<<
< (CT1s5x6[-5.855304718017578,0.9999058246612549:A-0.7025150872766972],)
< (CT1s6x6[-11.211071014404297,0.9910044074058533:A-1.6185989735854998],)
<<<
< (CT1s5x6[-7.473568439483643,2.216357707977295:A-0.68682375450929],)
< (CT1s6x6[-13.70550537109375,2.2497808933258057:A-1.797695554792881],)
<<<
The dynamic shapes are obtained with:
(({0: <_DimHint.DYNAMIC: 3>},), {})
Export¶
We use these dynamic shapes to export.
__call__ (
x |'<_ParameterKind.POSITIONAL_OR_KEYWORD: 1>'
)
dyn---: DYN0 -> WrapSym(DYN0)
dyn---: s0 -> WrapSym(s0)
dynrev: DYN0 -> [('DYN0', SymInt(DYN0))]
dynsrc: DYN0 -> [{DYN0:('input_name', 'x'), DYN0:('axis', 0)}]
dynals: s0 -> 'DYN0'
t-dynshp: 0 -> {0:(0, _Dim(DYN0))}
opset: : 18
input:: x |T1: DYN0 x 6
Add: x, x -> add |T1: DYN0 x 6 - add_Tensor
Mul: x, x -> mul |T1: DYN0 x 6 - mul_Tensor
Sub: add, mul -> sub |T1: DYN0 x 6 - sub_Tensor
Add: x, sub -> output_0 |T1: DYN0 x 6 - add_Tensor2
output:: output_0 |T1: DYN0 x 6
And visually.
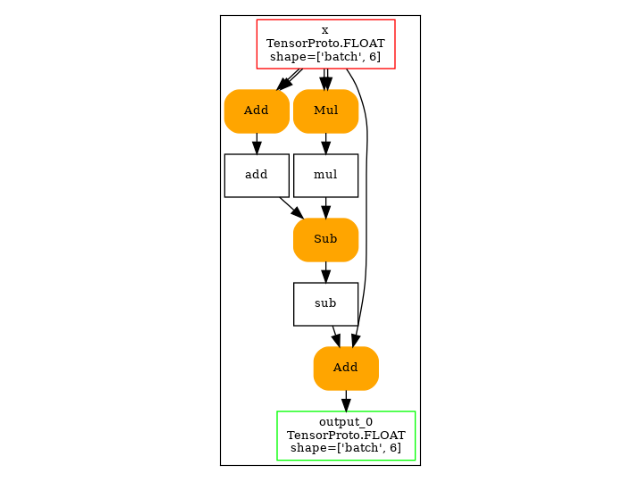
Total running time of the script: (0 minutes 0.152 seconds)
Related examples


