Compares implementations for a Piecewise Linear

A piecewise linear function is implemented and trained following the tutorial Custom C++ and CUDA Extensions.

Piecewise linear regression

import time
import pandas
import matplotlib.pyplot as plt
import torch
from teachcompute.torch_extensions.piecewise_linear import (
    PiecewiseLinearFunction,
    PiecewiseLinearFunctionC,
    PiecewiseLinearFunctionCBetter,
)


def train_piecewise_linear(x, y, device, cls, max_iter=400, learning_rate=1e-4):

    alpha_pos = torch.tensor([1], dtype=torch.float32).to(device)
    alpha_neg = torch.tensor([0.5], dtype=torch.float32).to(device)
    alpha_pos.requires_grad_()
    alpha_neg.requires_grad_()

    losses = []
    fct = cls.apply

    for _t in range(max_iter):

        y_pred = fct(x, alpha_neg, alpha_pos)
        loss = (y_pred - y).pow(2).sum()
        loss.backward()
        losses.append(loss)

        with torch.no_grad():
            alpha_pos -= learning_rate * alpha_pos.grad
            alpha_neg -= learning_rate * alpha_neg.grad

            # Manually zero the gradients after updating weights
            alpha_pos.grad.zero_()
            alpha_neg.grad.zero_()

    return losses, alpha_neg, alpha_pos

Python implementation

device = "cuda:0" if torch.cuda.is_available() else "cpu"
print("device:", device)
x = torch.randn(100, 1, dtype=torch.float32)
y = x * 0.2 + (x > 0).to(torch.float32) * x * 1.5 + torch.randn(100, 1) / 5
x = x.to(device).requires_grad_()
y = y.to(device).requires_grad_()

begin = time.perf_counter()
losses, alpha_neg, alpha_pos = train_piecewise_linear(
    x, y, device, PiecewiseLinearFunction
)
end = time.perf_counter()
print(f"duration={end - begin}, alpha_neg={alpha_neg} alpha_pos={alpha_pos}")

device: cuda:0
duration=1.1351559789982275, alpha_neg=tensor([0.2282], device='cuda:0', requires_grad=True) alpha_pos=tensor([1.6313], device='cuda:0', requires_grad=True)

C++ implementation

begin = time.perf_counter()
losses, alpha_neg, alpha_pos = train_piecewise_linear(
    x, y, device, PiecewiseLinearFunctionC
)
end = time.perf_counter()
print(f"duration={end - begin}, alpha_neg={alpha_neg} alpha_pos={alpha_pos}")

duration=0.7795067870029015, alpha_neg=tensor([0.2282], device='cuda:0', requires_grad=True) alpha_pos=tensor([1.6313], device='cuda:0', requires_grad=True)

C++ implementation, second try

begin = time.perf_counter()
losses, alpha_neg, alpha_pos = train_piecewise_linear(
    x, y, device, PiecewiseLinearFunctionCBetter
)
end = time.perf_counter()
print(f"duration={end - begin}, alpha_neg={alpha_neg} alpha_pos={alpha_pos}")

duration=0.8425100930035114, alpha_neg=tensor([0.2282], device='cuda:0', requires_grad=True) alpha_pos=tensor([1.6313], device='cuda:0', requires_grad=True)

The C++ implementation is very close to the python code. The second implementation in C++ is faster because it reuses created tensors.

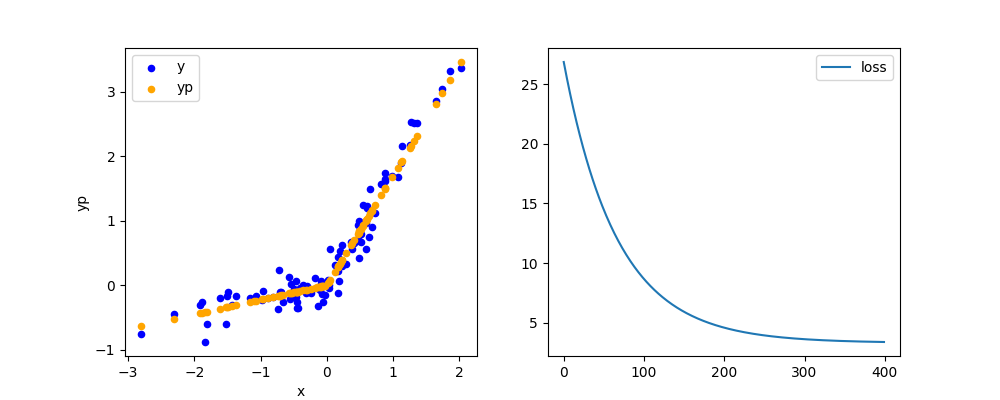
Graphs

df = pandas.DataFrame()
df["x"] = x.cpu().detach().numpy().ravel()
df["y"] = y.cpu().detach().numpy().ravel()
df["yp"] = PiecewiseLinearFunction.apply(x, alpha_neg, alpha_pos).cpu().detach().numpy()

fig, ax = plt.subplots(1, 2, figsize=(10, 4))
df.plot.scatter(x="x", y="y", label="y", color="blue", ax=ax[0])
df.plot.scatter(x="x", y="yp", ax=ax[0], label="yp", color="orange")
ax[1].plot([float(lo.detach()) for lo in losses], label="loss")
ax[1].legend()


# plt.show()

<matplotlib.legend.Legend object at 0x7f76e25f3490>