Note
Go to the end to download the full example code.
Compares matrix multiplication implementations¶
numpy has a very fast implementation of matrix multiplication. There are many ways to be slower.
Compared implementations:
import pprint
import numpy
from numpy.testing import assert_almost_equal
import matplotlib.pyplot as plt
from pandas import DataFrame, concat
from teachcompute.validation.cython.mul_cython_omp import dmul_cython_omp
from teachcompute.ext_test_case import measure_time_dim, unit_test_going
dfs = []
if unit_test_going():
sets = [2, 4, 6]
else:
sets = list(range(2, 145, 20))
numpy mul¶
ctxs = [
dict(
va=numpy.random.randn(n, n).astype(numpy.float64),
vb=numpy.random.randn(n, n).astype(numpy.float64),
mul=lambda x, y: x @ y,
x_name=n,
)
for n in sets
]
res = list(measure_time_dim("mul(va, vb)", ctxs, verbose=1))
dfs.append(DataFrame(res))
dfs[-1]["fct"] = "numpy"
pprint.pprint(dfs[-1].tail(n=2))
0%| | 0/8 [00:00<?, ?it/s]
100%|██████████| 8/8 [00:00<00:00, 45.89it/s]
100%|██████████| 8/8 [00:00<00:00, 45.79it/s]
average deviation min_exec max_exec repeat number ttime context_size warmup_time x_name fct
6 0.000068 0.000010 0.000057 0.000091 10 50 0.000677 184 0.000330 122 numpy
7 0.000148 0.000019 0.000124 0.000176 10 50 0.001481 184 0.000509 142 numpy
Simple multiplication¶
ctxs = [
dict(
va=numpy.random.randn(n, n).astype(numpy.float64),
vb=numpy.random.randn(n, n).astype(numpy.float64),
mul=dmul_cython_omp,
x_name=n,
)
for n in sets
]
res = list(measure_time_dim("mul(va, vb)", ctxs, verbose=1))
pprint.pprint(res[-1])
0%| | 0/8 [00:00<?, ?it/s]
50%|█████ | 4/8 [00:00<00:00, 26.29it/s]
88%|████████▊ | 7/8 [00:01<00:00, 4.46it/s]
100%|██████████| 8/8 [00:02<00:00, 3.29it/s]
{'average': np.float64(0.002170637821996934),
'context_size': 184,
'deviation': np.float64(0.00016493075762814832),
'max_exec': np.float64(0.0023841295799866204),
'min_exec': np.float64(0.0018377313399832928),
'number': 50,
'repeat': 10,
'ttime': np.float64(0.02170637821996934),
'warmup_time': 0.0017737540001689922,
'x_name': 142}
Other scenarios¶
3 differents algorithms, each of them parallelized.
See dmul_cython_omp.
for algo in range(2):
for parallel in (0, 1):
print("algo=%d parallel=%d" % (algo, parallel))
ctxs = [
dict(
va=numpy.random.randn(n, n).astype(numpy.float64),
vb=numpy.random.randn(n, n).astype(numpy.float64),
mul=lambda x, y, algo=algo, parallel=parallel: dmul_cython_omp(
x, y, algo=algo, parallel=parallel
),
x_name=n,
)
for n in sets
]
res = list(measure_time_dim("mul(va, vb)", ctxs, verbose=1))
dfs.append(DataFrame(res))
dfs[-1]["fct"] = "a=%d-p=%d" % (algo, parallel)
pprint.pprint(dfs[-1].tail(n=2))
algo=0 parallel=0
0%| | 0/8 [00:00<?, ?it/s]
50%|█████ | 4/8 [00:00<00:00, 29.62it/s]
88%|████████▊ | 7/8 [00:01<00:00, 4.60it/s]
100%|██████████| 8/8 [00:02<00:00, 3.41it/s]
average deviation min_exec max_exec repeat number ttime context_size warmup_time x_name fct
6 0.001293 0.000107 0.001110 0.001480 10 50 0.012928 184 0.001114 122 a=0-p=0
7 0.002087 0.000114 0.001895 0.002272 10 50 0.020871 184 0.001809 142 a=0-p=0
algo=0 parallel=1
0%| | 0/8 [00:00<?, ?it/s]
12%|█▎ | 1/8 [00:00<00:03, 2.13it/s]
25%|██▌ | 2/8 [00:00<00:02, 2.20it/s]
38%|███▊ | 3/8 [00:01<00:02, 2.28it/s]
50%|█████ | 4/8 [00:01<00:01, 2.24it/s]
62%|██████▎ | 5/8 [00:02<00:01, 2.19it/s]
75%|███████▌ | 6/8 [00:02<00:00, 2.08it/s]
88%|████████▊ | 7/8 [00:03<00:00, 1.89it/s]
100%|██████████| 8/8 [00:04<00:00, 1.74it/s]
100%|██████████| 8/8 [00:04<00:00, 1.96it/s]
average deviation min_exec max_exec repeat number ttime context_size warmup_time x_name fct
6 0.001251 0.000110 0.001084 0.001488 10 50 0.012507 184 0.002039 122 a=0-p=1
7 0.001331 0.000075 0.001209 0.001458 10 50 0.013310 184 0.001823 142 a=0-p=1
algo=1 parallel=0
0%| | 0/8 [00:00<?, ?it/s]
50%|█████ | 4/8 [00:00<00:00, 39.45it/s]
100%|██████████| 8/8 [00:02<00:00, 3.10it/s]
100%|██████████| 8/8 [00:02<00:00, 3.59it/s]
average deviation min_exec max_exec repeat number ttime context_size warmup_time x_name fct
6 0.001231 0.000136 0.001039 0.001492 10 50 0.012310 184 0.001038 122 a=1-p=0
7 0.002045 0.000129 0.001813 0.002221 10 50 0.020447 184 0.001809 142 a=1-p=0
algo=1 parallel=1
0%| | 0/8 [00:00<?, ?it/s]
12%|█▎ | 1/8 [00:00<00:02, 2.39it/s]
25%|██▌ | 2/8 [00:00<00:02, 2.43it/s]
38%|███▊ | 3/8 [00:01<00:02, 2.37it/s]
50%|█████ | 4/8 [00:01<00:01, 2.41it/s]
62%|██████▎ | 5/8 [00:02<00:01, 2.39it/s]
75%|███████▌ | 6/8 [00:02<00:00, 2.26it/s]
88%|████████▊ | 7/8 [00:03<00:00, 2.05it/s]
100%|██████████| 8/8 [00:03<00:00, 1.79it/s]
100%|██████████| 8/8 [00:03<00:00, 2.07it/s]
average deviation min_exec max_exec repeat number ttime context_size warmup_time x_name fct
6 0.001157 0.000115 0.000982 0.001342 10 50 0.011568 184 0.000849 122 a=1-p=1
7 0.001407 0.000050 0.001351 0.001495 10 50 0.014072 184 0.001894 142 a=1-p=1
One left issue¶
Will you find it in dmul_cython_omp.
va = numpy.random.randn(3, 4).astype(numpy.float64)
vb = numpy.random.randn(4, 5).astype(numpy.float64)
numpy_mul = va @ vb
try:
for a in range(50):
wrong_mul = dmul_cython_omp(va, vb, algo=2, parallel=1)
assert_almost_equal(numpy_mul, wrong_mul)
print("Iteration %d is Ok" % a)
print("All iterations are unexpectedly Ok. Don't push your luck.")
except AssertionError as e:
print(e)
Arrays are not almost equal to 7 decimals
Mismatched elements: 3 / 15 (20%)
Max absolute difference among violations: 2.25114336
Max relative difference among violations: inf
ACTUAL: array([[ 1.856174 , -1.0931995, 0.0351576, -0.8395243, -2.2511434],
[ 0.1621865, -1.0306951, -0.0106401, -0.1344068, -0.5930612],
[ 0.0509056, -0.4700069, 0.6167465, 1.8928914, 0.6949332]])
DESIRED: array([[ 1.856174 , -1.0931995, 0.0351576, -0.8395243, 0. ],
[ 0.1621865, -1.0306951, -0.0106401, -0.1344068, 0. ],
[ 0.0509056, -0.4700069, 0.6167465, 1.8928914, 0. ]])
Other scenarios but transposed¶
Same differents algorithms but the second matrix
is transposed first: b_trans=1.
for algo in range(2):
for parallel in (0, 1):
print("algo=%d parallel=%d transposed" % (algo, parallel))
ctxs = [
dict(
va=numpy.random.randn(n, n).astype(numpy.float64),
vb=numpy.random.randn(n, n).astype(numpy.float64),
mul=lambda x, y, parallel=parallel, algo=algo: dmul_cython_omp(
x, y, algo=algo, parallel=parallel, b_trans=1
),
x_name=n,
)
for n in sets
]
res = list(measure_time_dim("mul(va, vb)", ctxs, verbose=2))
dfs.append(DataFrame(res))
dfs[-1]["fct"] = "a=%d-p=%d-T" % (algo, parallel)
pprint.pprint(dfs[-1].tail(n=2))
algo=0 parallel=0 transposed
0%| | 0/8 [00:00<?, ?it/s]
62%|██████▎ | 5/8 [00:00<00:00, 23.97it/s]
100%|██████████| 8/8 [00:01<00:00, 4.95it/s]
100%|██████████| 8/8 [00:01<00:00, 5.82it/s]
average deviation min_exec max_exec repeat number ttime context_size warmup_time x_name fct
6 0.000694 0.000072 0.000619 0.000872 10 50 0.006942 184 0.000543 122 a=0-p=0-T
7 0.001214 0.000118 0.000984 0.001374 10 50 0.012143 184 0.000984 142 a=0-p=0-T
algo=0 parallel=1 transposed
0%| | 0/8 [00:00<?, ?it/s]
75%|███████▌ | 6/8 [00:00<00:00, 40.11it/s]
100%|██████████| 8/8 [00:00<00:00, 22.66it/s]
average deviation min_exec max_exec repeat number ttime context_size warmup_time x_name fct
6 0.000161 0.000005 0.000150 0.000169 10 50 0.001614 184 0.000188 122 a=0-p=1-T
7 0.000241 0.000010 0.000229 0.000257 10 50 0.002414 184 0.000251 142 a=0-p=1-T
algo=1 parallel=0 transposed
0%| | 0/8 [00:00<?, ?it/s]
62%|██████▎ | 5/8 [00:00<00:00, 26.75it/s]
100%|██████████| 8/8 [00:01<00:00, 5.47it/s]
100%|██████████| 8/8 [00:01<00:00, 6.43it/s]
average deviation min_exec max_exec repeat number ttime context_size warmup_time x_name fct
6 0.000677 0.000038 0.000613 0.000727 10 50 0.006774 184 0.000957 122 a=1-p=0-T
7 0.001026 0.000097 0.000935 0.001245 10 50 0.010255 184 0.000851 142 a=1-p=0-T
algo=1 parallel=1 transposed
0%| | 0/8 [00:00<?, ?it/s]
75%|███████▌ | 6/8 [00:00<00:00, 43.79it/s]
100%|██████████| 8/8 [00:00<00:00, 23.43it/s]
average deviation min_exec max_exec repeat number ttime context_size warmup_time x_name fct
6 0.000160 0.000007 0.000151 0.000173 10 50 0.001599 184 0.000183 122 a=1-p=1-T
7 0.000245 0.000004 0.000240 0.000252 10 50 0.002453 184 0.000266 142 a=1-p=1-T
Let’s display the results¶
cc = concat(dfs)
cc["N"] = cc["x_name"]
fig, ax = plt.subplots(3, 2, figsize=(10, 8), sharex=True, sharey=True)
ccnp = cc.fct == "numpy"
cct = cc.fct.str.contains("-T")
cca0 = cc.fct.str.contains("a=0")
cc[ccnp | (~cct & cca0)].pivot(index="N", columns="fct", values="average").plot(
logy=True, logx=True, ax=ax[0, 0]
)
cc[ccnp | (~cct & ~cca0)].pivot(index="N", columns="fct", values="average").plot(
logy=True, logx=True, ax=ax[0, 1]
)
cc[ccnp | (cct & cca0)].pivot(index="N", columns="fct", values="average").plot(
logy=True, logx=True, ax=ax[1, 0]
)
cc[ccnp | (~cct & ~cca0)].pivot(index="N", columns="fct", values="average").plot(
logy=True, logx=True, ax=ax[1, 1]
)
cc[ccnp | cca0].pivot(index="N", columns="fct", values="average").plot(
logy=True, logx=True, ax=ax[2, 0]
)
cc[ccnp | ~cca0].pivot(index="N", columns="fct", values="average").plot(
logy=True, logx=True, ax=ax[2, 1]
)
fig.suptitle("Comparison of matrix multiplication implementations")
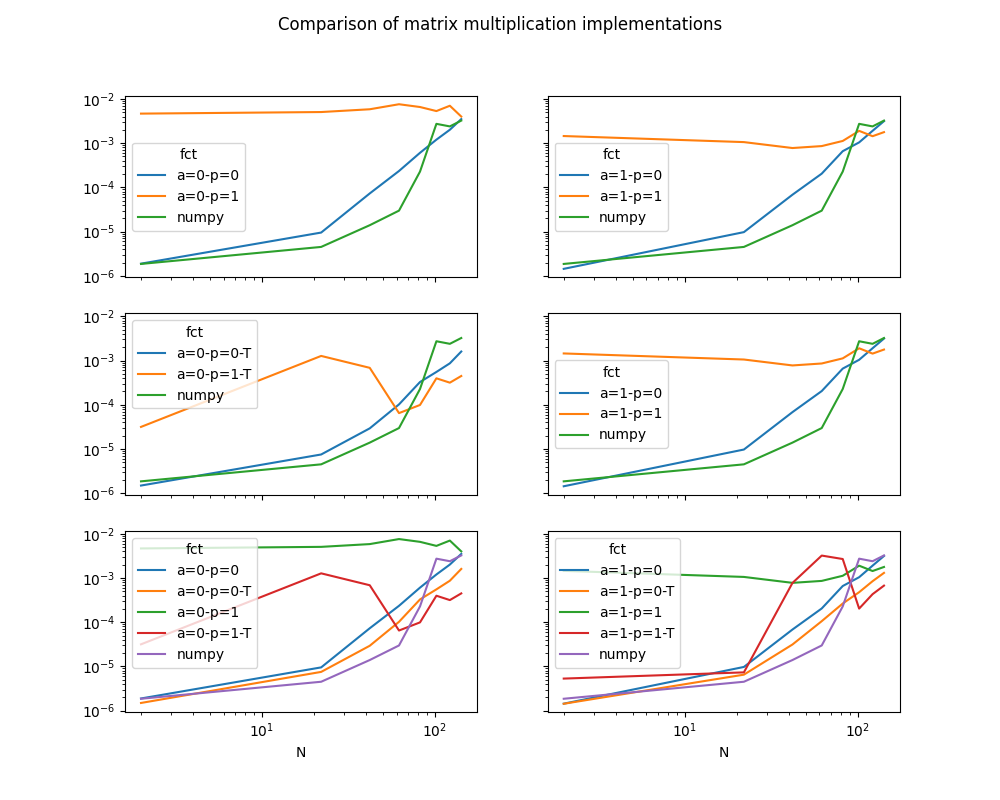
Text(0.5, 0.98, 'Comparison of matrix multiplication implementations')
The results depends on the machine, its number of cores, the compilation settings of numpy or this module.
Total running time of the script: (0 minutes 19.817 seconds)