Compares dot implementations (numpy, python, blas)¶

numpy has a very fast implementation of the dot product. It is difficult to be better and very easy to be slower. This example looks into a couple of slower implementations.

Compared implementations:

import pprint
import numpy
import matplotlib.pyplot as plt
from pandas import DataFrame, concat
from teachcompute.validation.cython.dotpy import pydot
from teachcompute.validation.cython.dot_blas_lapack import cblas_ddot
from teachcompute.ext_test_case import measure_time_dim

python dot: pydot¶

The first function pydot uses python to implement the dot product.

ctxs = [
    dict(
        va=numpy.random.randn(n).astype(numpy.float64),
        vb=numpy.random.randn(n).astype(numpy.float64),
        pydot=pydot,
        x_name=n,
    )
    for n in range(10, 1000, 100)
]

res_pydot = list(measure_time_dim("pydot(va, vb)", ctxs, verbose=1))

pprint.pprint(res_pydot[:2])

  0%|          | 0/10 [00:00<?, ?it/s]
 60%|██████    | 6/10 [00:00<00:00, 41.99it/s]
100%|██████████| 10/10 [00:00<00:00, 23.65it/s]
[{'average': np.float64(3.4828960087907036e-06),
  'context_size': 184,
  'deviation': np.float64(2.5366880209299793e-07),
  'max_exec': np.float64(3.9840200042817744e-06),
  'min_exec': np.float64(3.2468399876961483e-06),
  'number': 50,
  'repeat': 10,
  'ttime': np.float64(3.4828960087907036e-05),
  'warmup_time': 2.464600038365461e-05,
  'x_name': 10},
 {'average': np.float64(2.1452124005008953e-05),
  'context_size': 184,
  'deviation': np.float64(1.0212164147243848e-06),
  'max_exec': np.float64(2.3413800008711405e-05),
  'min_exec': np.float64(1.997549999941839e-05),
  'number': 50,
  'repeat': 10,
  'ttime': np.float64(0.00021452124005008952),
  'warmup_time': 2.8200000087963417e-05,
  'x_name': 110}]

numpy dot¶

ctxs = [
    dict(
        va=numpy.random.randn(n).astype(numpy.float64),
        vb=numpy.random.randn(n).astype(numpy.float64),
        dot=numpy.dot,
        x_name=n,
    )
    for n in range(10, 50000, 100)
]

res_dot = list(measure_time_dim("dot(va, vb)", ctxs, verbose=1))

pprint.pprint(res_dot[:2])

  0%|          | 0/500 [00:00<?, ?it/s]
 17%|█▋        | 87/500 [00:00<00:00, 864.60it/s]
 17%|█▋        | 87/500 [00:19<00:00, 864.60it/s]
 23%|██▎       | 114/500 [00:19<01:26,  4.46it/s]
 23%|██▎       | 115/500 [00:20<01:27,  4.42it/s]
 30%|███       | 151/500 [00:25<01:07,  5.18it/s]
 34%|███▍      | 171/500 [00:26<00:49,  6.65it/s]
 37%|███▋      | 185/500 [00:26<00:39,  8.04it/s]
 39%|███▉      | 195/500 [00:28<00:40,  7.52it/s]
 40%|████      | 202/500 [00:28<00:36,  8.16it/s]
 42%|████▏     | 208/500 [00:28<00:31,  9.37it/s]
 44%|████▎     | 218/500 [00:29<00:23, 12.22it/s]
 45%|████▌     | 227/500 [00:29<00:19, 13.65it/s]
 47%|████▋     | 237/500 [00:29<00:14, 17.99it/s]
 49%|████▊     | 243/500 [00:29<00:14, 17.44it/s]
 50%|████▉     | 248/500 [00:30<00:14, 16.98it/s]
 50%|█████     | 252/500 [00:30<00:13, 18.14it/s]
 51%|█████     | 256/500 [00:30<00:12, 18.93it/s]
 52%|█████▏    | 260/500 [00:30<00:11, 20.64it/s]
 54%|█████▎    | 268/500 [00:30<00:08, 28.95it/s]
 56%|█████▌    | 279/500 [00:31<00:07, 27.93it/s]
 57%|█████▋    | 283/500 [00:31<00:08, 24.34it/s]
 58%|█████▊    | 291/500 [00:31<00:06, 30.84it/s]
 60%|██████    | 302/500 [00:31<00:04, 43.30it/s]
 62%|██████▏   | 309/500 [00:31<00:04, 47.56it/s]
 64%|██████▍   | 320/500 [00:32<00:05, 30.05it/s]
 67%|██████▋   | 333/500 [00:32<00:03, 42.55it/s]
 69%|██████▉   | 344/500 [00:32<00:04, 35.49it/s]
 71%|███████   | 353/500 [00:33<00:03, 38.73it/s]
 72%|███████▏  | 361/500 [00:33<00:03, 44.34it/s]
 74%|███████▎  | 368/500 [00:33<00:02, 47.82it/s]
 76%|███████▌  | 380/500 [00:33<00:01, 61.44it/s]
 78%|███████▊  | 388/500 [00:33<00:01, 61.87it/s]
 79%|███████▉  | 396/500 [00:33<00:01, 61.53it/s]
 81%|████████  | 404/500 [00:33<00:01, 53.54it/s]
 83%|████████▎ | 415/500 [00:34<00:01, 63.92it/s]
 85%|████████▍ | 423/500 [00:34<00:01, 61.88it/s]
 86%|████████▌ | 430/500 [00:34<00:01, 41.98it/s]
 87%|████████▋ | 436/500 [00:34<00:01, 39.21it/s]
 89%|████████▉ | 446/500 [00:34<00:01, 49.07it/s]
 91%|█████████ | 453/500 [00:34<00:00, 50.26it/s]
 92%|█████████▏| 459/500 [00:36<00:03, 12.73it/s]
 93%|█████████▎| 464/500 [00:36<00:02, 14.96it/s]
 95%|█████████▍| 474/500 [00:36<00:01, 22.31it/s]
 97%|█████████▋| 483/500 [00:36<00:00, 26.36it/s]
 98%|█████████▊| 489/500 [00:38<00:00, 11.99it/s]
 99%|█████████▊| 493/500 [00:38<00:00, 13.65it/s]
100%|██████████| 500/500 [00:38<00:00, 12.99it/s]
[{'average': np.float64(6.94043996190885e-07),
  'context_size': 184,
  'deviation': np.float64(1.597944197806861e-07),
  'max_exec': np.float64(1.1711600018315949e-06),
  'min_exec': np.float64(6.276199928834103e-07),
  'number': 50,
  'repeat': 10,
  'ttime': np.float64(6.94043996190885e-06),
  'warmup_time': 1.8733000615611672e-05,
  'x_name': 10},
 {'average': np.float64(6.549579920829274e-07),
  'context_size': 184,
  'deviation': np.float64(6.312012639755665e-08),
  'max_exec': np.float64(8.427599823335186e-07),
  'min_exec': np.float64(6.272799873840995e-07),
  'number': 50,
  'repeat': 10,
  'ttime': np.float64(6.549579920829274e-06),
  'warmup_time': 3.6579986044671386e-06,
  'x_name': 110}]

blas dot¶

numpy implementation uses BLAS. Let’s make a direct call to it.

for ctx in ctxs:
    ctx["ddot"] = cblas_ddot

res_ddot = list(measure_time_dim("ddot(va, vb)", ctxs, verbose=1))

pprint.pprint(res_ddot[:2])

  0%|          | 0/500 [00:00<?, ?it/s]
 11%|█▏        | 57/500 [00:00<00:00, 567.47it/s]
 23%|██▎       | 114/500 [00:00<00:03, 108.27it/s]
 28%|██▊       | 142/500 [00:01<00:03, 96.07it/s]
 32%|███▏      | 161/500 [00:01<00:03, 93.77it/s]
 35%|███▌      | 176/500 [00:01<00:03, 87.21it/s]
 38%|███▊      | 188/500 [00:04<00:13, 22.30it/s]
 40%|████      | 200/500 [00:04<00:11, 26.77it/s]
 42%|████▏     | 209/500 [00:04<00:10, 28.56it/s]
 43%|████▎     | 217/500 [00:04<00:08, 31.52it/s]
 45%|████▍     | 224/500 [00:04<00:08, 32.22it/s]
 46%|████▌     | 230/500 [00:04<00:08, 33.15it/s]
 47%|████▋     | 236/500 [00:04<00:07, 36.29it/s]
 48%|████▊     | 242/500 [00:05<00:07, 33.33it/s]
 51%|█████     | 253/500 [00:05<00:05, 44.78it/s]
 52%|█████▏    | 260/500 [00:05<00:06, 38.91it/s]
 53%|█████▎    | 267/500 [00:05<00:05, 44.11it/s]
 55%|█████▍    | 273/500 [00:06<00:07, 29.96it/s]
 57%|█████▋    | 283/500 [00:06<00:05, 40.03it/s]
 58%|█████▊    | 292/500 [00:06<00:04, 47.11it/s]
 60%|██████    | 300/500 [00:06<00:03, 52.18it/s]
 61%|██████▏   | 307/500 [00:06<00:04, 40.43it/s]
 63%|██████▎   | 313/500 [00:06<00:04, 38.43it/s]
 64%|██████▍   | 321/500 [00:06<00:03, 45.08it/s]
 65%|██████▌   | 327/500 [00:07<00:05, 30.06it/s]
 66%|██████▋   | 332/500 [00:07<00:07, 21.10it/s]
 68%|██████▊   | 338/500 [00:07<00:06, 23.86it/s]
 68%|██████▊   | 342/500 [00:08<00:06, 23.68it/s]
 69%|██████▉   | 347/500 [00:08<00:05, 25.71it/s]
 70%|███████   | 352/500 [00:08<00:05, 28.82it/s]
 73%|███████▎  | 363/500 [00:08<00:03, 43.54it/s]
 74%|███████▍  | 369/500 [00:08<00:04, 29.07it/s]
 76%|███████▌  | 379/500 [00:09<00:03, 39.51it/s]
 77%|███████▋  | 385/500 [00:09<00:02, 39.49it/s]
 78%|███████▊  | 391/500 [00:09<00:02, 41.02it/s]
 79%|███████▉  | 397/500 [00:09<00:02, 39.07it/s]
 82%|████████▏ | 408/500 [00:09<00:01, 52.90it/s]
 83%|████████▎ | 416/500 [00:09<00:01, 58.70it/s]
 85%|████████▌ | 425/500 [00:09<00:01, 65.25it/s]
 87%|████████▋ | 433/500 [00:09<00:01, 61.62it/s]
 88%|████████▊ | 440/500 [00:10<00:01, 58.84it/s]
 90%|█████████ | 450/500 [00:10<00:00, 68.41it/s]
 92%|█████████▏| 458/500 [00:10<00:00, 44.63it/s]
 93%|█████████▎| 464/500 [00:10<00:01, 35.57it/s]
 94%|█████████▍| 469/500 [00:10<00:00, 37.62it/s]
 95%|█████████▌| 476/500 [00:11<00:00, 41.27it/s]
 96%|█████████▌| 481/500 [00:11<00:00, 33.15it/s]
 98%|█████████▊| 488/500 [00:11<00:00, 37.79it/s]
 99%|█████████▊| 493/500 [00:11<00:00, 31.53it/s]
 99%|█████████▉| 497/500 [00:11<00:00, 32.51it/s]
100%|██████████| 500/500 [00:11<00:00, 41.98it/s]
[{'average': np.float64(2.361988001212012e-06),
  'context_size': 272,
  'deviation': np.float64(1.5673665338115333e-07),
  'max_exec': np.float64(2.732800021476578e-06),
  'min_exec': np.float64(2.2530199930770324e-06),
  'number': 50,
  'repeat': 10,
  'ttime': np.float64(2.361988001212012e-05),
  'warmup_time': 0.00014882799951010384,
  'x_name': 10},
 {'average': np.float64(2.394110004388494e-06),
  'context_size': 272,
  'deviation': np.float64(1.57056619999441e-07),
  'max_exec': np.float64(2.8635800117626786e-06),
  'min_exec': np.float64(2.3153800066211263e-06),
  'number': 50,
  'repeat': 10,
  'ttime': np.float64(2.3941100043884943e-05),
  'warmup_time': 6.681000741082244e-06,
  'x_name': 110}]

Let’s display the results¶

df1 = DataFrame(res_pydot)
df1["fct"] = "pydot"
df2 = DataFrame(res_dot)
df2["fct"] = "numpy.dot"
df3 = DataFrame(res_ddot)
df3["fct"] = "ddot"

cc = concat([df1, df2, df3])
cc["N"] = cc["x_name"]

fig, ax = plt.subplots(1, 2, figsize=(10, 4))
cc[cc.N <= 1100].pivot(index="N", columns="fct", values="average").plot(
    logy=True, logx=True, ax=ax[0]
)
cc[cc.fct != "pydot"].pivot(index="N", columns="fct", values="average").plot(
    logy=True, logx=True, ax=ax[1]
)
ax[0].set_title("Comparison of dot implementations")
ax[1].set_title("Comparison of dot implementations\nwithout python")

Comparison of dot implementations, Comparison of dot implementations without python

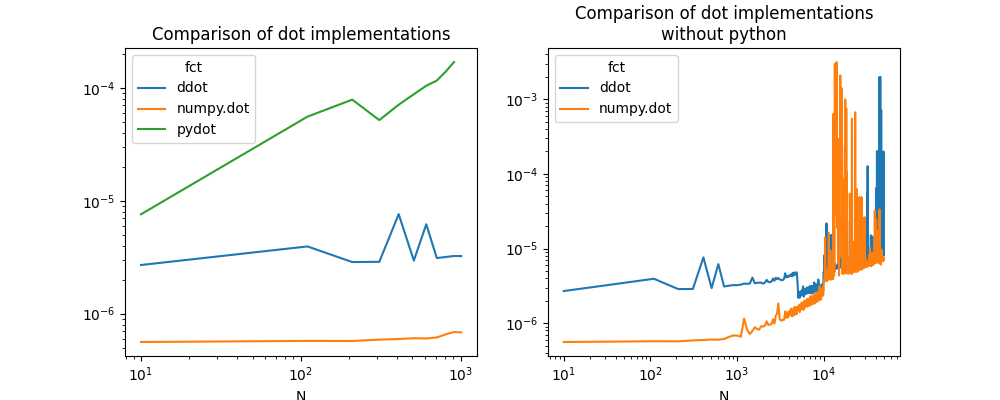
Text(0.5, 1.0, 'Comparison of dot implementations\nwithout python')

The results depends on the machine, its number of cores, the compilation settings of numpy or this module.

Total running time of the script: (0 minutes 52.577 seconds)

Gallery generated by Sphinx-Gallery