Compares implementations of Einsum

This example compares different equations for function numpy.einsum(). It compares numpy implementation to a custom implementation, onnxruntime implementation and opt-einsum optimisation. If available, tensorflow and pytorch are included as well. The custom implementation does not do any transpose. It uses parallelisation and SIMD optimization when the summation happens on the last axis of both matrices. It only implements matrix multiplication. We also measure the improvment made with function einsum.

Available optimisation

The code shows which optimisation is used for the custom implementation, AVX or SSE and the number of available processors, equal to the default number of used threads to parallelize.

import logging
import numpy
import pandas
import matplotlib.pyplot as plt
from onnx import TensorProto
from onnx.helper import (
    make_model,
    make_graph,
    make_node,
    make_tensor_value_info,
    make_opsetid,
)
from onnxruntime import InferenceSession
from onnx_extended.ext_test_case import measure_time, unit_test_going
from tqdm import tqdm
from opt_einsum import contract
from onnx_extended.tools.einsum.einsum_fct import _einsum

logging.getLogger("matplotlib.font_manager").setLevel(logging.ERROR)
logging.getLogger("matplotlib.ticker").setLevel(logging.ERROR)
logging.getLogger("PIL.PngImagePlugin").setLevel(logging.ERROR)
logging.getLogger("onnx-extended").setLevel(logging.ERROR)

Einsum: common code

try:
    from tensorflow import einsum as tf_einsum, convert_to_tensor
except ImportError:
    tf_einsum = None
try:
    from torch import einsum as torch_einsum, from_numpy
except ImportError:
    torch_einsum = None


def build_ort_einsum(equation, op_version=18):  # opset=13, 14, ...
    onx = make_model(
        make_graph(
            [make_node("Einsum", ["x", "y"], ["z"], equation=equation)],
            equation,
            [
                make_tensor_value_info("x", TensorProto.FLOAT, None),
                make_tensor_value_info("y", TensorProto.FLOAT, None),
            ],
            [make_tensor_value_info("z", TensorProto.FLOAT, None)],
        ),
        opset_imports=[make_opsetid("", op_version)],
        ir_version=9,
    )
    sess = InferenceSession(onx.SerializeToString(), providers=["CPUExecutionProvider"])
    return lambda x, y: sess.run(None, {"x": x, "y": y})


def build_ort_decomposed(equation, op_version=18):  # opset=13, 14, ...
    cache = _einsum(
        equation,
        numpy.float32,
        opset=op_version,
        optimize=True,
        verbose=True,
        runtime="python",
    )
    if not hasattr(cache, "onnx_"):
        cache.build()
    sess = InferenceSession(
        cache.onnx_.SerializeToString(), providers=["CPUExecutionProvider"]
    )
    return lambda x, y: sess.run(None, {"X0": x, "X1": y})


def loop_einsum_eq(fct, equation, xs, ys):
    for x, y in zip(xs, ys):
        fct(equation, x, y)


def loop_einsum_eq_th(fct, equation, xs, ys):
    for x, y in zip(xs, ys):
        fct(equation, x, y, nthread=-1)


def loop_einsum(fct, xs, ys):
    for x, y in zip(xs, ys):
        fct(x, y)


def timeit(stmt, ctx, dim, name):
    obs = measure_time(stmt, div_by_number=True, context=ctx, repeat=5, number=1)
    obs["dim"] = dim
    obs["fct"] = name
    return obs


def benchmark_equation(equation):
    # equations
    ort_einsum = build_ort_einsum(equation)
    ort_einsum_decomposed = build_ort_decomposed(equation)
    res = []
    for dim in tqdm([8, 16, 32, 64, 100, 128, 200, 256]):  # , 500, 512]):
        if unit_test_going() and dim > 64:
            break
        xs = [numpy.random.rand(2, dim, 12, 64).astype(numpy.float32) for _ in range(5)]
        ys = [numpy.random.rand(2, dim, 12, 64).astype(numpy.float32) for _ in range(5)]

        # numpy
        ctx = dict(
            equation=equation,
            xs=xs,
            ys=ys,
            einsum=numpy.einsum,
            loop_einsum=loop_einsum,
            loop_einsum_eq=loop_einsum_eq,
            loop_einsum_eq_th=loop_einsum_eq_th,
        )
        obs = timeit(
            "loop_einsum_eq(einsum, equation, xs, ys)", ctx, dim, "numpy.einsum"
        )
        res.append(obs)

        # opt-einsum
        ctx["einsum"] = contract
        obs = timeit("loop_einsum_eq(einsum, equation, xs, ys)", ctx, dim, "opt-einsum")
        res.append(obs)

        # onnxruntime
        ctx["einsum"] = ort_einsum
        obs = timeit("loop_einsum(einsum, xs, ys)", ctx, dim, "ort-einsum")
        res.append(obs)

        # onnxruntime decomposed
        ctx["einsum"] = ort_einsum_decomposed
        obs = timeit("loop_einsum(einsum, xs, ys)", ctx, dim, "ort-dec")
        res.append(obs)

        if tf_einsum is not None:
            # tensorflow
            ctx["einsum"] = tf_einsum
            ctx["xs"] = [convert_to_tensor(x) for x in xs]
            ctx["ys"] = [convert_to_tensor(y) for y in ys]
            obs = timeit(
                "loop_einsum_eq(einsum, equation, xs, ys)", ctx, dim, "tf-einsum"
            )
            res.append(obs)

        if torch_einsum is not None:
            # torch
            ctx["einsum"] = torch_einsum
            ctx["xs"] = [from_numpy(x) for x in xs]
            ctx["ys"] = [from_numpy(y) for y in ys]
            obs = timeit(
                "loop_einsum_eq(einsum, equation, xs, ys)", ctx, dim, "torch-einsum"
            )
            res.append(obs)

    # Dataframes
    df = pandas.DataFrame(res)
    piv = df.pivot(index="dim", columns="fct", values="average")

    rs = piv.copy()
    for c in ["ort-einsum", "ort-dec", "tf-einsum", "torch-einsum", "opt-einsum"]:
        if c not in rs.columns:
            continue
        rs[c] = rs["numpy.einsum"] / rs[c]
    rs["numpy.einsum"] = 1.0

    # Graphs.
    fig, ax = plt.subplots(1, 2, figsize=(14, 5))
    piv.plot(
        logx=True,
        logy=True,
        ax=ax[0],
        title=f"Einsum benchmark\n{equation} -- (2, N, 12, 64) lower better",
    )
    ax[0].legend(prop={"size": 9})
    rs.plot(
        logx=True,
        logy=True,
        ax=ax[1],
        title="Einsum Speedup, baseline=numpy\n%s -- (2, N, 12, 64)"
        " higher better" % equation,
    )
    ax[1].plot([min(rs.index), max(rs.index)], [0.5, 0.5], "g--")
    ax[1].plot([min(rs.index), max(rs.index)], [2.0, 2.0], "g--")
    ax[1].legend(prop={"size": 9})

    return df, rs, ax

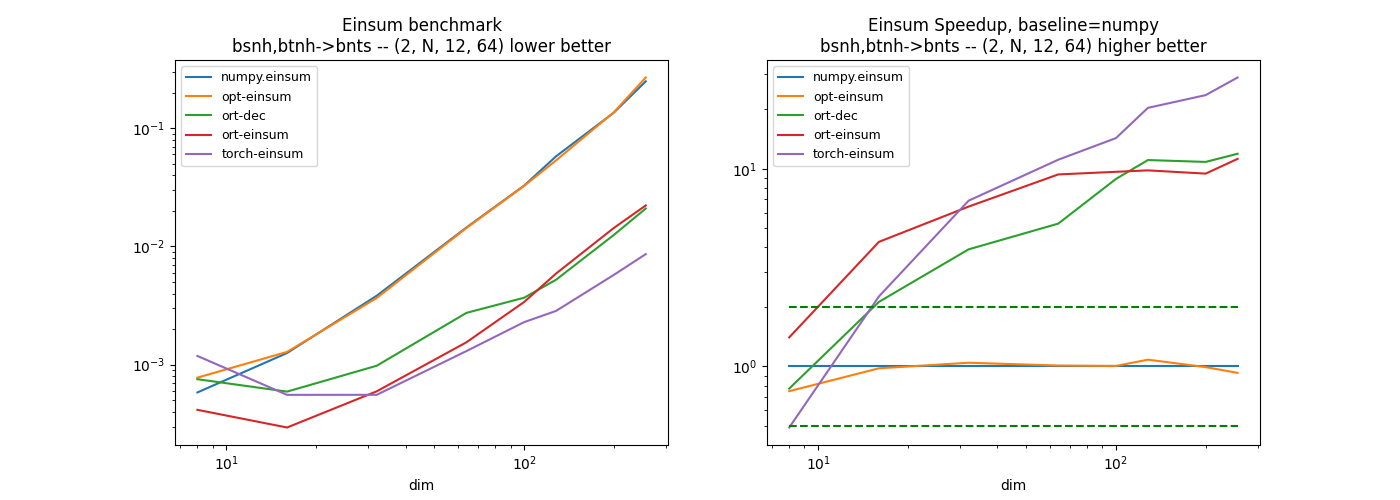
First equation: bsnh,btnh->bnts

The decomposition of this equation without einsum function gives the following.

dfs = []
equation = "bsnh,btnh->bnts"
df, piv, ax = benchmark_equation(equation)
df.pivot(index="fct", columns="dim", values="average")
dfs.append(df)

  0%|          | 0/121 [00:00<?, ?it/s]
0.0092 rtbest='bsnh,btnh->bnts':   0%|          | 0/121 [00:00<?, ?it/s]
0.0084 rtbest='bsnh,btnh->bnts':   0%|          | 0/121 [00:00<?, ?it/s]
0.0076 rtbest='btnh,bsnh->bnst':   0%|          | 0/121 [00:00<?, ?it/s]
0.0076 rtbest='btnh,bsnh->bnst':   3%|▎         | 4/121 [00:00<00:03, 38.64it/s]
0.0074 rtbest='btsh,bnsh->bsnt':   3%|▎         | 4/121 [00:00<00:03, 38.64it/s]
0.0069 rtbest='bthn,bshn->bhst':   3%|▎         | 4/121 [00:00<00:03, 38.64it/s]
0.0069 rtbest='bthn,bshn->bhst':  12%|█▏        | 14/121 [00:00<00:01, 73.89it/s]
0.0069 rtbest='bthn,bshn->bhst':  21%|██        | 25/121 [00:00<00:01, 88.14it/s]
0.0069 rtbest='bthn,bshn->bhst':  30%|██▉       | 36/121 [00:00<00:00, 93.27it/s]
0.0069 rtbest='bthn,bshn->bhst':  39%|███▉      | 47/121 [00:00<00:00, 98.26it/s]
0.0069 rtbest='bthn,bshn->bhst':  48%|████▊     | 58/121 [00:00<00:00, 100.92it/s]
0.0069 rtbest='bthn,bshn->bhst':  57%|█████▋    | 69/121 [00:00<00:00, 101.89it/s]
0.0069 rtbest='bthn,bshn->bhst':  66%|██████▌   | 80/121 [00:00<00:00, 102.05it/s]
0.0069 rtbest='bthn,bshn->bhst':  75%|███████▌  | 91/121 [00:00<00:00, 101.98it/s]
0.0069 rtbest='bthn,bshn->bhst':  84%|████████▍ | 102/121 [00:01<00:00, 103.50it/s]
0.0069 rtbest='bthn,bshn->bhst':  93%|█████████▎| 113/121 [00:01<00:00, 102.89it/s]
0.0069 rtbest='bthn,bshn->bhst': 100%|██████████| 121/121 [00:01<00:00, 98.00it/s]

  0%|          | 0/8 [00:00<?, ?it/s]
 25%|██▌       | 2/8 [00:00<00:00, 15.78it/s]
 50%|█████     | 4/8 [00:00<00:00,  9.13it/s]
 75%|███████▌  | 6/8 [00:01<00:00,  2.90it/s]
 88%|████████▊ | 7/8 [00:03<00:00,  1.39it/s]
100%|██████████| 8/8 [00:06<00:00,  1.43s/it]
100%|██████████| 8/8 [00:06<00:00,  1.15it/s]

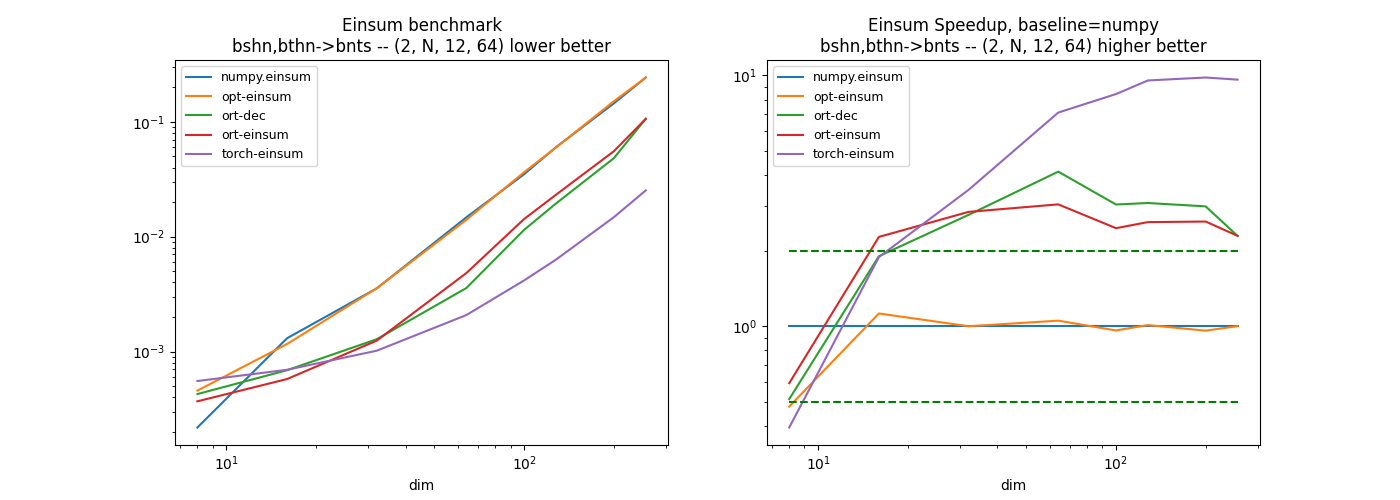
Second equation: bshn,bthn->bnts

The summation does not happen on the last axis but on the previous one. Is it worth transposing before doing the summation… The decomposition of this equation without einsum function gives the following.

equation = "bshn,bthn->bnts"
df, piv, ax = benchmark_equation(equation)
df.pivot(index="fct", columns="dim", values="average")
dfs.append(df)

  0%|          | 0/121 [00:00<?, ?it/s]
0.016 rtbest='bshn,bthn->bnts':   0%|          | 0/121 [00:00<?, ?it/s]
0.0099 rtbest='bshn,bthn->bnts':   0%|          | 0/121 [00:00<?, ?it/s]
0.009 rtbest='bsht,bnht->btns':   0%|          | 0/121 [00:00<?, ?it/s]
0.009 rtbest='bsht,bnht->btns':   6%|▌         | 7/121 [00:00<00:01, 68.23it/s]
0.0089 rtbest='bsnh,btnh->bhts':   6%|▌         | 7/121 [00:00<00:01, 68.23it/s]
0.0089 rtbest='bsnh,btnh->bhts':  12%|█▏        | 14/121 [00:00<00:01, 62.63it/s]
0.0087 rtbest='btsn,bhsn->bnht':  12%|█▏        | 14/121 [00:00<00:01, 62.63it/s]
0.0087 rtbest='btsn,bhsn->bnht':  18%|█▊        | 22/121 [00:00<00:01, 69.56it/s]
0.0086 rtbest='htbn,hsbn->hnst':  18%|█▊        | 22/121 [00:00<00:01, 69.56it/s]
0.0079 rtbest='hnbs,htbs->hstn':  18%|█▊        | 22/121 [00:00<00:01, 69.56it/s]
0.0077 rtbest='hnbt,hsbt->htsn':  18%|█▊        | 22/121 [00:00<00:01, 69.56it/s]
0.0074 rtbest='htbs,hnbs->hsnt':  18%|█▊        | 22/121 [00:00<00:01, 69.56it/s]
0.0074 rtbest='htbs,hnbs->hsnt':  26%|██▋       | 32/121 [00:00<00:01, 78.31it/s]
0.0072 rtbest='snbh,stbh->shtn':  26%|██▋       | 32/121 [00:00<00:01, 78.31it/s]
0.0068 rtbest='shbt,snbt->stnh':  26%|██▋       | 32/121 [00:00<00:01, 78.31it/s]
0.0068 rtbest='shbt,snbt->stnh':  36%|███▌      | 43/121 [00:00<00:00, 86.76it/s]
0.0068 rtbest='shbt,snbt->stnh':  45%|████▍     | 54/121 [00:00<00:00, 93.27it/s]
0.0068 rtbest='shbt,snbt->stnh':  53%|█████▎    | 64/121 [00:00<00:00, 92.29it/s]
0.0068 rtbest='shbt,snbt->stnh':  63%|██████▎   | 76/121 [00:00<00:00, 98.15it/s]
0.0068 rtbest='hbtn,hstn->hnsb':  63%|██████▎   | 76/121 [00:00<00:00, 98.15it/s]
0.0068 rtbest='hbtn,hstn->hnsb':  73%|███████▎  | 88/121 [00:00<00:00, 102.24it/s]
0.0068 rtbest='nbts,nhts->nshb':  73%|███████▎  | 88/121 [00:01<00:00, 102.24it/s]
0.0068 rtbest='htns,hbns->hsbt':  73%|███████▎  | 88/121 [00:01<00:00, 102.24it/s]
0.0068 rtbest='htns,hbns->hsbt':  82%|████████▏ | 99/121 [00:01<00:00, 103.49it/s]
0.0067 rtbest='hnst,hbst->htbn':  82%|████████▏ | 99/121 [00:01<00:00, 103.49it/s]
0.0067 rtbest='hnst,hbst->htbn':  91%|█████████ | 110/121 [00:01<00:00, 104.08it/s]
0.0067 rtbest='hnst,hbst->htbn': 100%|██████████| 121/121 [00:01<00:00, 105.51it/s]
0.0067 rtbest='hnst,hbst->htbn': 100%|██████████| 121/121 [00:01<00:00, 94.58it/s]

  0%|          | 0/8 [00:00<?, ?it/s]
 38%|███▊      | 3/8 [00:00<00:00, 25.42it/s]
 75%|███████▌  | 6/8 [00:02<00:00,  2.56it/s]
100%|██████████| 8/8 [00:08<00:00,  1.50s/it]
100%|██████████| 8/8 [00:08<00:00,  1.12s/it]

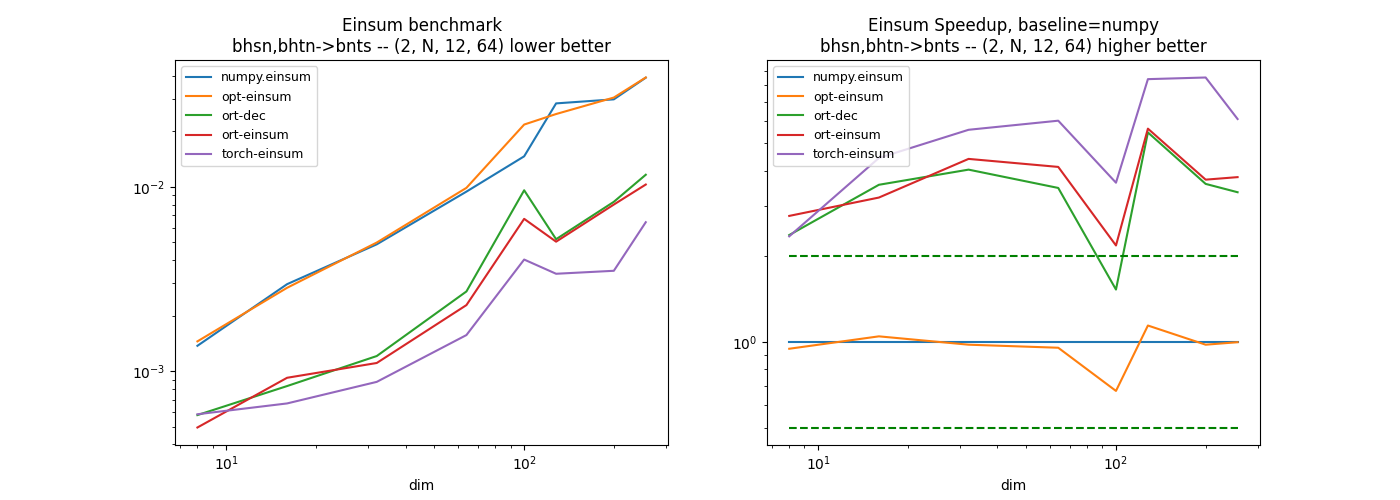
Third equation: bhsn,bhtn->bnts

The summation does not happen on the last axis but on the second one. It is worth transposing before multiplying. The decomposition of this equation without einsum function gives the following.

equation = "bhsn,bhtn->bnts"
df, piv, ax = benchmark_equation(equation)
df.pivot(index="fct", columns="dim", values="average")
dfs.append(df)

  0%|          | 0/121 [00:00<?, ?it/s]
0.0091 rtbest='bhsn,bhtn->bnts':   0%|          | 0/121 [00:00<?, ?it/s]
0.0091 rtbest='bhsn,bhtn->bnts':   7%|▋         | 8/121 [00:00<00:01, 76.97it/s]
0.009 rtbest='bsth,bsnh->bhnt':   7%|▋         | 8/121 [00:00<00:01, 76.97it/s]
0.009 rtbest='bnhs,bnts->bsth':   7%|▋         | 8/121 [00:00<00:01, 76.97it/s]
0.0089 rtbest='bnht,bnst->btsh':   7%|▋         | 8/121 [00:00<00:01, 76.97it/s]
0.0089 rtbest='bnht,bnst->btsh':  14%|█▍        | 17/121 [00:00<00:01, 82.32it/s]
0.0089 rtbest='bnht,bnst->btsh':  21%|██▏       | 26/121 [00:00<00:01, 83.27it/s]
0.0089 rtbest='bnht,bnst->btsh':  29%|██▉       | 35/121 [00:00<00:01, 83.89it/s]
0.0089 rtbest='bnht,bnst->btsh':  36%|███▋      | 44/121 [00:00<00:00, 85.03it/s]
0.0089 rtbest='bnht,bnst->btsh':  44%|████▍     | 53/121 [00:00<00:00, 85.12it/s]
0.0089 rtbest='bnht,bnst->btsh':  51%|█████     | 62/121 [00:00<00:00, 85.64it/s]
0.0089 rtbest='bnht,bnst->btsh':  59%|█████▊    | 71/121 [00:00<00:00, 83.92it/s]
0.0089 rtbest='bnht,bnst->btsh':  66%|██████▌   | 80/121 [00:00<00:00, 78.29it/s]
0.008 rtbest='ntbh,ntsh->nhsb':  66%|██████▌   | 80/121 [00:01<00:00, 78.29it/s]
0.0077 rtbest='snbh,snth->shtb':  66%|██████▌   | 80/121 [00:01<00:00, 78.29it/s]
0.0076 rtbest='tnbh,tnsh->thsb':  66%|██████▌   | 80/121 [00:01<00:00, 78.29it/s]
0.0076 rtbest='tnbh,tnsh->thsb':  74%|███████▎  | 89/121 [00:01<00:00, 81.42it/s]
0.0075 rtbest='nsbt,nsht->nthb':  74%|███████▎  | 89/121 [00:01<00:00, 81.42it/s]
0.0075 rtbest='nsbt,nsht->nthb':  82%|████████▏ | 99/121 [00:01<00:00, 85.03it/s]
0.0074 rtbest='shnt,shbt->stbn':  82%|████████▏ | 99/121 [00:01<00:00, 85.03it/s]
0.0074 rtbest='shnt,shbt->stbn':  91%|█████████ | 110/121 [00:01<00:00, 90.32it/s]
0.0073 rtbest='nsht,nsbt->ntbh':  91%|█████████ | 110/121 [00:01<00:00, 90.32it/s]
0.0072 rtbest='nths,ntbs->nsbh':  91%|█████████ | 110/121 [00:01<00:00, 90.32it/s]
0.0072 rtbest='nths,ntbs->nsbh': 100%|██████████| 121/121 [00:01<00:00, 95.05it/s]
0.0072 rtbest='nths,ntbs->nsbh': 100%|██████████| 121/121 [00:01<00:00, 86.68it/s]

  0%|          | 0/8 [00:00<?, ?it/s]
 38%|███▊      | 3/8 [00:00<00:00, 17.74it/s]
 62%|██████▎   | 5/8 [00:00<00:00,  6.51it/s]
 75%|███████▌  | 6/8 [00:01<00:00,  4.43it/s]
 88%|████████▊ | 7/8 [00:01<00:00,  3.32it/s]
100%|██████████| 8/8 [00:02<00:00,  2.47it/s]
100%|██████████| 8/8 [00:02<00:00,  3.49it/s]

Conclusion

pytorch seems quite efficient on these examples. The custom implementation was a way to investigate the implementation of einsum and find some ways to optimize it.

merged = pandas.concat(dfs)
name = "einsum"
merged.to_csv(f"plot_{name}.csv", index=False)
merged.to_excel(f"plot_{name}.xlsx", index=False)
plt.savefig(f"plot_{name}.png")

# plt.show()