Quantile MLPRegressor

scikit-learn does not have a quantile regression for multi-layer perceptron. mlinsights implements a version of it based on the scikit-learn model. The implementation overwrites method _backprop.

We first generate some dummy data.

import numpy
from pandas import DataFrame
import matplotlib.pyplot as plt
from sklearn.neural_network import MLPRegressor
from mlinsights.mlmodel import QuantileMLPRegressor


X = numpy.random.random(1000)
eps1 = (numpy.random.random(900) - 0.5) * 0.1
eps2 = (numpy.random.random(100)) * 10
eps = numpy.hstack([eps1, eps2])
X = X.reshape((1000, 1))
Y = X.ravel() * 3.4 + 5.6 + eps

clr = MLPRegressor(hidden_layer_sizes=(30,), activation="tanh")
clr.fit(X, Y)

MLPRegressor(activation='tanh', hidden_layer_sizes=(30,))

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

clq = QuantileMLPRegressor(hidden_layer_sizes=(30,), activation="tanh")
clq.fit(X, Y)

QuantileMLPRegressor(activation='tanh', hidden_layer_sizes=(30,))

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

data = dict(X=X.ravel(), Y=Y, clr=clr.predict(X), clq=clq.predict(X))
df = DataFrame(data)
df.head()

	X	Y	clr	clq
0	0.379957	6.937997	7.492150	6.949007
1	0.076410	5.860495	6.348967	5.788681
2	0.292278	6.559855	7.178483	6.630396
3	0.755102	8.211254	8.671232	8.156544
4	0.637990	7.733815	8.331789	7.806592

fig, ax = plt.subplots(1, 1, figsize=(10, 4))
choice = numpy.random.choice(X.shape[0] - 1, size=100)
xx = X.ravel()[choice]
yy = Y[choice]
ax.plot(xx, yy, ".", label="data")
xx = numpy.array([[0], [1]])
y1 = clr.predict(xx)
y2 = clq.predict(xx)
ax.plot(xx, y1, "--", label="L2")
ax.plot(xx, y2, "--", label="L1")
ax.set_title("Quantile (L1) vs Square (L2) for MLPRegressor")
ax.legend()

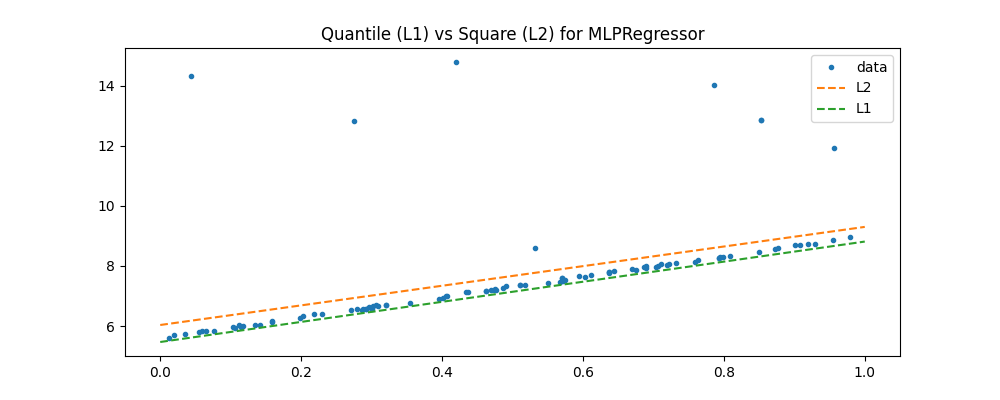
<matplotlib.legend.Legend object at 0x7f75565b6c80>