Reproducible Parallelized Reduction is difficult¶

A reduction is a frequent operation with neural networks. It appears in layer normalization, softmax… Because of the float precision, the result of the computation changes based on the order of the elements. The following examples show the variation based on different hypothesis on the vector distribution. We consider a vector $X = (x_1, ..., x_n)$ . It computes the average:

$mean(X) = \frac{\sum_{i=1}^n x_i}{n}$

Or the normalization of the vector:

$norm(X)_i = \frac{ X_i - \mathbb{E}X}{ \sqrt{ \mathbb{V}X}}$

With $\mathbb{E}X = mean(X)$ , $\mathbb{V}X = mean\left(\left(X - mean(X)\right)^2\right)$ . We draw 128 random permutations of X. The average or mean should not change. And the normalized vector should have the same values. In the first case, we compute the difference between the highest and the lowest values obtained for the average. In the second case, we look for the maximum difference between the original normalized vector and the permuted one, both sorted.

The computation code¶

import itertools
from tqdm import tqdm
import numpy as np
import pandas

DATA = []


def str_dtype(dtype):
    """Displays numpy dtype in a nicer way."""
    if dtype == np.float64:
        return "fp64"
    if dtype == np.float32:
        return "fp32"
    if dtype == np.float16:
        return "fp16"
    raise ValueError(f"Unexpected value {dtype}")


def layer_norm(a, eps=1e-6):
    """
    Normalized the vector a.
    The computation is done in float32 or float64.
    """
    ctype = np.float32 if a.dtype == np.float16 else a.dtype
    a32 = a.astype(ctype)
    m = a32.mean(axis=-1, keepdims=True)
    c = a32 - m
    va = np.sqrt((c * c).mean(axis=-1, keepdims=True))
    va += eps
    return (c / va).astype(a.dtype)


def compute(values, fct):
    """
    Compare the results of function ``fct`` on a sample.
    Loops over multiple sizes, dtypes. Tries 128 times.
    """

    def make_value(base, value):
        if value.size > 1:
            return np.abs(np.sort(base) - np.sort(value)).max()
        return value

    sizes = [2, 4, 8, 16, 512, 1024, 2048, 4096, 8192]
    dtypes = [np.float64, np.float32, np.float16]
    N = list(range(128))
    exps = list(itertools.product(sizes, dtypes, N))
    data = []
    ech = None
    for size, dtype, n in tqdm(exps):
        if n == 0:
            ech = values[:size].astype(dtype)
            base = fct(ech)
            assert base.dtype == ech.dtype
            obs = dict(
                n=n, size=size, dtype=str_dtype(ech.dtype), value=make_value(base, fct(ech))
            )
            data.append(obs)

        if n == 1:
            new_ech = np.sort(ech)
        elif n == 2:
            new_ech = np.sort(ech)[::-1]
        else:
            new_ech = np.random.permutation(ech)
        assert new_ech.dtype == ech.dtype
        assert new_ech.shape == ech.shape
        obs = dict(
            n=n + 1,
            size=size,
            dtype=str_dtype(new_ech.dtype),
            value=make_value(base, fct(new_ech)),
        )
        data.append(obs)

    df = pandas.DataFrame(data)
    agg = df.drop("n", axis=1).groupby(["dtype", "size"], as_index=False).agg(["min", "max"])
    agg["value", "delta"] = agg["value", "max"] - agg["value", "min"]
    piv = agg.pivot(index="size", columns="dtype", values=("value", "delta"))
    return piv

Normal Law¶

Let’s see what it returns an on random sample following a normal law. First the average.

values = np.random.randn(4096)
mean = compute(values, lambda x: np.mean(x).astype(x.dtype))
mean["name"] = "normal"
print(mean)

  0%|          | 0/3456 [00:00<?, ?it/s]
 95%|█████████▍| 3275/3456 [00:00<00:00, 32733.56it/s]
100%|██████████| 3456/3456 [00:00<00:00, 29419.14it/s]
dtype  fp16          fp32          fp64    name
size
2       0.0  0.000000e+00  0.000000e+00  normal
4       0.0  2.980232e-08  0.000000e+00  normal
8       0.0  4.470348e-08  1.110223e-16  normal
16      0.0  4.470348e-08  1.110223e-16  normal
512     0.0  3.911555e-08  7.285839e-17  normal
1024    0.0  3.166497e-08  7.112366e-17  normal
2048    0.0  7.357448e-08  3.035766e-17  normal
4096    0.0  3.166497e-08  8.500145e-17  normal
8192    0.0  3.213063e-08  8.413409e-17  normal

Then the layer normalization.

ln = compute(values, layer_norm)
ln["name"] = "normal"
DATA.append(ln.reset_index(drop=True).max(axis=0))
print(ln)

  0%|          | 0/3456 [00:00<?, ?it/s]
 70%|██████▉   | 2412/3456 [00:00<00:00, 24111.97it/s]
100%|██████████| 3456/3456 [00:00<00:00, 7924.62it/s]
dtype  fp16          fp32          fp64    name
size
2       0.0  0.000000e+00  0.000000e+00  normal
4       0.0  2.980232e-08  2.220446e-16  normal
8       0.0  1.192093e-07  2.220446e-16  normal
16      0.0  2.384186e-07  4.440892e-16  normal
512     0.0  2.384186e-07  4.440892e-16  normal
1024    0.0  2.384186e-07  4.440892e-16  normal
2048    0.0  2.384186e-07  4.440892e-16  normal
4096    0.0  2.384186e-07  4.440892e-16  normal
8192    0.0  2.384186e-07  4.440892e-16  normal

Fixed values¶

We try a fixed vector with one very high value and all the others are small.

values[:] = -1e-4
values[::128] = 100
mean = compute(values, lambda x: np.mean(x).astype(x.dtype))
mean["name"] = "fixed"
print(mean)

  0%|          | 0/3456 [00:00<?, ?it/s]
 99%|█████████▉| 3417/3456 [00:00<00:00, 34147.16it/s]
100%|██████████| 3456/3456 [00:00<00:00, 33216.27it/s]
dtype  fp16          fp32          fp64   name
size
2       0.0  0.000000e+00  0.000000e+00  fixed
4       0.0  0.000000e+00  3.552714e-15  fixed
8       0.0  0.000000e+00  0.000000e+00  fixed
16      0.0  0.000000e+00  0.000000e+00  fixed
512     0.0  2.384186e-07  4.440892e-16  fixed
1024    0.0  2.980232e-07  4.440892e-16  fixed
2048    0.0  4.768372e-07  4.440892e-16  fixed
4096    0.0  2.384186e-07  9.992007e-16  fixed
8192    0.0  2.980232e-07  9.992007e-16  fixed

And the normalized vector.

ln = compute(values, layer_norm)
ln["name"] = "fixed"
DATA.append(ln.reset_index(drop=True).max(axis=0))
print(ln)

  0%|          | 0/3456 [00:00<?, ?it/s]
 72%|███████▏  | 2474/3456 [00:00<00:00, 24721.34it/s]
100%|██████████| 3456/3456 [00:00<00:00, 12200.92it/s]
dtype  fp16      fp32          fp64   name
size
2       0.0  0.000000  0.000000e+00  fixed
4       0.0  0.000000  2.220446e-16  fixed
8       0.0  0.000000  0.000000e+00  fixed
16      0.0  0.000000  0.000000e+00  fixed
512     0.0  0.000002  1.776357e-15  fixed
1024    0.0  0.000002  1.776357e-15  fixed
2048    0.0  0.000004  7.105427e-15  fixed
4096    0.0  0.000002  1.776357e-15  fixed
8192    0.0  0.000002  1.776357e-15  fixed

Pareto Distribution¶

A law with a long tail.

values = np.random.pareto(1, (4096,))
print(values)

mean = compute(values, lambda x: np.mean(x).astype(x.dtype))
mean["name"] = "normal"
print(mean)

[20.31721071  2.09292762  1.05623266 ... 15.6123532   2.43049564
  1.18719163]

  0%|          | 0/3456 [00:00<?, ?it/s]
 93%|█████████▎| 3214/3456 [00:00<00:00, 32130.53it/s]
100%|██████████| 3456/3456 [00:00<00:00, 27493.04it/s]
dtype  fp16          fp32          fp64    name
size
2       0.0  0.000000e+00  0.000000e+00  normal
4       0.0  4.768372e-07  0.000000e+00  normal
8       0.0  2.384186e-07  4.440892e-16  normal
16      0.0  4.768372e-07  8.881784e-16  normal
512     0.0  2.861023e-06  3.552714e-15  normal
1024    0.0  9.536743e-07  3.552714e-15  normal
2048    0.0  9.536743e-07  2.664535e-15  normal
4096    0.0  9.536743e-07  1.776357e-15  normal
8192    0.0  1.907349e-06  1.776357e-15  normal

And the normalized vector.

ln = compute(values, layer_norm)
ln["name"] = "pareto"
DATA.append(ln.reset_index(drop=True).max(axis=0))
print(ln)

  0%|          | 0/3456 [00:00<?, ?it/s]
 74%|███████▍  | 2557/3456 [00:00<00:00, 25557.35it/s]
100%|██████████| 3456/3456 [00:00<00:00, 8311.26it/s]
dtype      fp16          fp32          fp64    name
size
2      0.000000  0.000000e+00  0.000000e+00  pareto
4      0.000000  2.384186e-07  0.000000e+00  pareto
8      0.000000  2.384186e-07  4.440892e-16  pareto
16     0.000000  4.768372e-07  4.440892e-16  pareto
512    0.000000  1.907349e-06  3.552714e-15  pareto
1024   0.000000  7.629395e-06  7.105427e-15  pareto
2048   0.000008  7.629395e-06  7.105427e-15  pareto
4096   0.000031  3.814697e-06  1.421085e-14  pareto
8192   0.000031  3.814697e-06  1.421085e-14  pareto

Summary¶

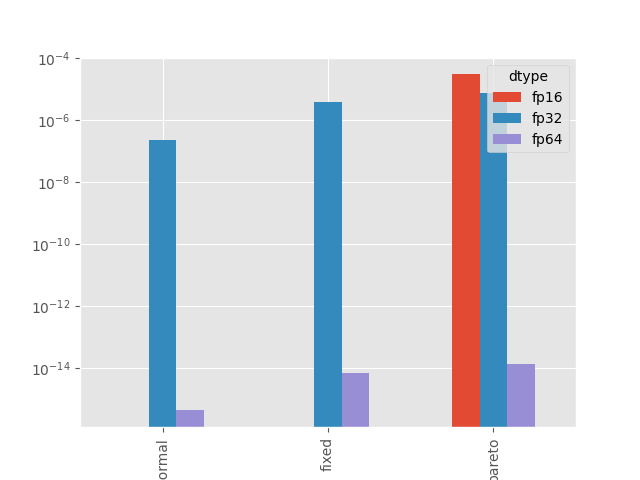
We consider the maximum difference obtained for any sample size.

df = pandas.DataFrame(DATA).set_index("name")
print(df)

dtype       fp16          fp32          fp64
name
normal  0.000000  2.384186e-07  4.440892e-16
fixed   0.000000  3.814697e-06  7.105427e-15
pareto  0.000031  7.629395e-06  1.421085e-14

Visually.

ax = df.plot.bar(logy=True)
fig = ax.get_figure()
fig.savefig("plot_parallelized_reduction.png")

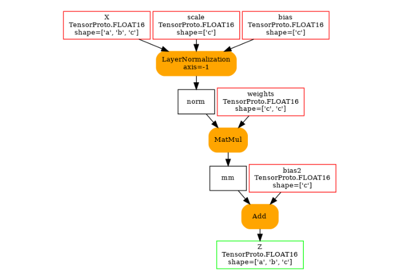
In a deep neural network¶

Some of the vector have 500 values, 16x32x1024x1024. A layer normalization does 16x32x1024 ~ 2M reductions, over 20 layers. When a deep neural network is computed with a different code doing a different parallelization (GPU/CPU for example), the order of the reduction may change and therefore, some errors will appear and propagate.

Total running time of the script: (0 minutes 2.143 seconds)

Related examples

Gallery generated by Sphinx-Gallery