2048 et les classes#
Le jeu 2048 est assez addictif mais peut-on imaginer une stratégie qui joue à notre place est maximise le gain… Le jeu se joue sur une matrice 4x4.
Décomposition du problème#
Création de la matrice de jeu
Ajout d’un nombre aléatoire dans
{2,4}à une position aléatoire pourvu qu’elle soit libreDétermination de toutes les cases libres
A-t-on perdu ?
Joue un coup sachant une direction donnée
Aggrège les nombres dans un tableau que ce soit une ligne ou une colonne
Score…
Choisit le coup suivant (un coup au hasard selon deux directions possibles)
Joue une partie en appelant toutes les fonctions précédentes.
0 - Création de la matrice de jeu#
[1]:
import numpy
def creer_jeu(dim):
return numpy.zeros((dim, dim), dtype=int)
jeu = creer_jeu(4)
jeu
[1]:
array([[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0]])
2 - Détermination de toutes les cases libres#
[2]:
def position_libre(jeu):
pos = []
for i in range(jeu.shape[0]):
for j in range(jeu.shape[1]):
if jeu[i, j] == 0:
pos.append((i, j))
return pos
position_libre(jeu)
[2]:
[(0, 0),
(0, 1),
(0, 2),
(0, 3),
(1, 0),
(1, 1),
(1, 2),
(1, 3),
(2, 0),
(2, 1),
(2, 2),
(2, 3),
(3, 0),
(3, 1),
(3, 2),
(3, 3)]
1 - Ajout d’un nombre aléatoire dans {2,4} à une position aléatoire pourvu qu’elle soit libre#
[3]:
def nombre_aleatoire(jeu):
pos = position_libre(jeu)
nb = numpy.random.randint(0, 2) * 2 + 2
i = numpy.random.randint(0, len(pos))
p = pos[i]
jeu[p] = nb
nombre_aleatoire(jeu)
jeu
[3]:
array([[0, 0, 2, 0],
[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0]])
3 - A-t-on perdu ?#
[4]:
def perdu(jeu):
pos = position_libre(jeu)
return len(pos) == 0
perdu(jeu)
[4]:
False
5 - Aggrège les nombres dans un tableau que ce soit une ligne ou une colonne#
[5]:
def joue_ligne_colonne(lc):
# on enlève les 0
non_null = [a for a in lc if a != 0]
# on additionne les nombres identiques consécutifs
i = len(non_null) - 1
while i > 0:
if non_null[i] != 0 and non_null[i] == non_null[i - 1]:
non_null[i - 1] *= 2
non_null[i] = 0
i -= 2
else:
i -= 1
# on enlève à nouveau les zéros
non_null2 = [a for a in non_null if a != 0]
final = numpy.zeros(len(lc), dtype=int)
final[: len(non_null2)] = non_null2
return final
joue_ligne_colonne(numpy.array([2, 4, 2, 2]))
[5]:
array([2, 4, 4, 0])
[6]:
assert joue_ligne_colonne(numpy.array([0, 2, 0, 2])).tolist() == [4, 0, 0, 0]
assert joue_ligne_colonne(numpy.array([2, 2, 2, 2])).tolist() == [4, 4, 0, 0]
assert joue_ligne_colonne(numpy.array([2, 4, 2, 2])).tolist() == [2, 4, 4, 0]
4 - Joue un coup sachant une direction donnée#
[7]:
def joue_coup(jeu, direction):
if direction == 0: # gauche
for i in range(jeu.shape[0]):
jeu[i, :] = joue_ligne_colonne(jeu[i, :])
elif direction == 1: # droite
for i in range(jeu.shape[0]):
jeu[i, ::-1] = joue_ligne_colonne(jeu[i, ::-1])
elif direction == 2: # haut
for i in range(jeu.shape[0]):
jeu[:, i] = joue_ligne_colonne(jeu[:, i])
elif direction == 3: # bas
for i in range(jeu.shape[0]):
jeu[::-1, i] = joue_ligne_colonne(jeu[::-1, i])
joue_coup(jeu, 0)
jeu
[7]:
array([[2, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0]])
6 - score#
[8]:
def score(jeu):
return jeu.max()
# à ne pas confondre avec max(jeu)
# max(jeu) appelle la fonction max de python (et non celle du numpy),
# elle cherche le maximum sur toutes les lignes
# et comparer deux lignes est ambigü, comparaison terme à terme ? ce n'est pas un ordre total
score(jeu)
[8]:
2
Voir ordre total.
7 - coup suivant#
[9]:
def coup_suivant(jeu):
# une direction aléatoire parmi 0 ou 4
h = numpy.random.randint(0, 2)
return h * 2
coup_suivant(jeu)
[9]:
0
8 - la fonction faisant tout#
[10]:
def partie(dim):
jeu = creer_jeu(dim)
coup = 0
while not perdu(jeu):
nombre_aleatoire(jeu)
d = coup_suivant(jeu)
joue_coup(jeu, d)
coup += 1
return coup, jeu
coup, jeu = partie(4)
print("nombre de coups: %d, score=%d jeu:" % (coup, score(jeu)))
print(jeu)
nombre de coups: 63, score=64 jeu:
[[ 2 64 2 4]
[32 4 16 2]
[ 2 32 8 8]
[ 8 2 4 2]]
Classes#
[11]:
class c2048:
def __init__(self, dim=4):
self.jeu = self.creer_jeu(dim)
self.coup = 0
self.score = 0
def creer_jeu(self, dim):
return creer_jeu(dim)
def __repr__(self):
return "coup=%d score=%d, jeu=\n%s" % (self.coup, self.score, self.jeu)
J = c2048()
J
[11]:
coup=0 score=0, jeu=
[[0 0 0 0]
[0 0 0 0]
[0 0 0 0]
[0 0 0 0]]
[12]:
print(J) # l'interpréteur python exécute implicitement : print(J.__repr__())
coup=0 score=0, jeu=
[[0 0 0 0]
[0 0 0 0]
[0 0 0 0]
[0 0 0 0]]
Classe complète#
[13]:
class c2048:
def __init__(self, dim=4):
self.jeu = self.creer_jeu(dim)
self.coup = 0
self.score = 0
def creer_jeu(self, dim):
return creer_jeu(dim)
def __repr__(self):
return "coup=%d score=%d, jeu=\n%s" % (self.coup, self.score, self.jeu)
def position_libre(self):
pos = []
for i in range(self.jeu.shape[0]):
for j in range(self.jeu.shape[1]):
if self.jeu[i, j] == 0:
pos.append((i, j))
return pos
def calcule_score(self):
return self.jeu.max()
def joue_ligne_colonne(self, lc):
# on enlève les 0
non_null = [a for a in lc if a != 0]
# on additionne les nombres identiques consécutifs
i = len(non_null) - 1
while i > 0:
if non_null[i] != 0 and non_null[i] == non_null[i - 1]:
non_null[i - 1] *= 2
non_null[i] = 0
i -= 2
else:
i -= 1
# on enlève à nouveau les zéros
non_null2 = [a for a in non_null if a != 0]
final = numpy.zeros(len(lc), dtype=int)
final[: len(non_null2)] = non_null2
return final
def joue_coup(self, direction):
if direction == 0: # gauche
for i in range(self.jeu.shape[0]):
self.jeu[i, :] = joue_ligne_colonne(self.jeu[i, :])
elif direction == 1: # droite
for i in range(self.jeu.shape[0]):
self.jeu[i, ::-1] = joue_ligne_colonne(self.jeu[i, ::-1])
# identique à
# self.jeu[i, :] = joue_ligne_colonne(self.jeu[i, ::-1])[::-1]
elif direction == 2: # haut
for i in range(self.jeu.shape[0]):
self.jeu[:, i] = joue_ligne_colonne(self.jeu[:, i])
elif direction == 3: # bas
for i in range(self.jeu.shape[0]):
self.jeu[::-1, i] = joue_ligne_colonne(self.jeu[::-1, i])
def nombre_aleatoire(self):
pos = self.position_libre()
nb = numpy.random.randint(0, 2) * 2 + 2
i = numpy.random.randint(0, len(pos))
p = pos[i]
self.jeu[p] = nb
def perdu(self):
pos = self.position_libre()
return len(pos) == 0
def coup_suivant(self):
# une direction aléatoire parmi 0 ou 4
h = numpy.random.randint(0, 2)
return h * 2
def partie(self):
self.coup = 0
while not self.perdu():
self.nombre_aleatoire()
d = self.coup_suivant()
self.joue_coup(d)
self.coup += 1
self.score = self.calcule_score()
J = c2048()
J.partie()
J
[13]:
coup=47 score=32, jeu=
[[32 16 2 16]
[16 4 32 4]
[ 4 2 8 4]
[ 2 8 4 2]]
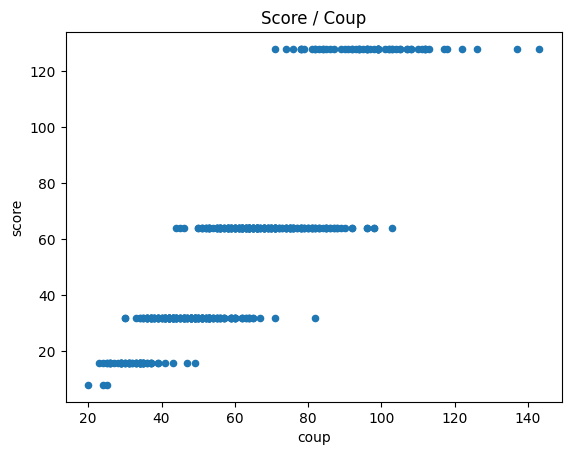
Un dernier graphe pour finir#
On réalise plusieurs parties, on trace un graphe avec le nombre de coups en abscisse et le score en ordonnée.
[14]:
from tqdm import tqdm
from pandas import DataFrame
obs = []
for i in tqdm(range(500)):
J = c2048()
J.partie()
obs.append(dict(score=J.score, coup=J.coup))
df = DataFrame(obs)
df.head()
35%|███▌ | 176/500 [00:03<00:05, 58.62it/s]100%|██████████| 500/500 [00:07<00:00, 65.84it/s]
[14]:
| score | coup | |
|---|---|---|
| 0 | 64 | 60 |
| 1 | 128 | 99 |
| 2 | 64 | 54 |
| 3 | 32 | 54 |
| 4 | 64 | 72 |
[15]:
df.plot(x="coup", y="score", kind="scatter", title="Score / Coup");
Une autre stratégie pour illustrer l’héritage#
On veut essayer une autre stratégie et la comparer avec la précédente. Pour cela, on crée une seconde classe dans laquelle on remplace la méthode coup_suivant. On pourrait tout copier coller mais c’est très souvent la plus mauvaise option. Et pour éviter cela, on crée une seconde classe qui hérite de la précédente, puis on remplace la méthode souhaitée.
[16]:
class c2048_4(c2048):
def coup_suivant(self):
# une direction aléatoire parmi 0 ou 4
h = numpy.random.randint(0, 3)
return h
obs = []
for i in tqdm(range(500)):
J = c2048()
J.partie()
obs.append(dict(score=J.score, coup=J.coup))
df2 = DataFrame(obs)
df2.head()
100%|██████████| 500/500 [00:05<00:00, 94.51it/s]
[16]:
| score | coup | |
|---|---|---|
| 0 | 16 | 37 |
| 1 | 64 | 71 |
| 2 | 64 | 64 |
| 3 | 64 | 64 |
| 4 | 64 | 55 |
[17]:
import matplotlib.pyplot as plt
fig, ax = plt.subplots(2, 2, figsize=(14, 4), sharey=True, sharex=True)
df.plot(
x="coup",
y="score",
kind="scatter",
title="Score / Coup",
label="Stratégie 1",
ax=ax[0, 0],
)
df2.plot(
x="coup",
y="score",
kind="scatter",
title="Score / Coup",
label="Stratégie 2",
ax=ax[1, 0],
color="red",
)
df2.plot(
x="coup",
y="score",
kind="scatter",
title="Score / Coup",
label="Stratégie 2",
ax=ax[0, 1],
color="red",
);
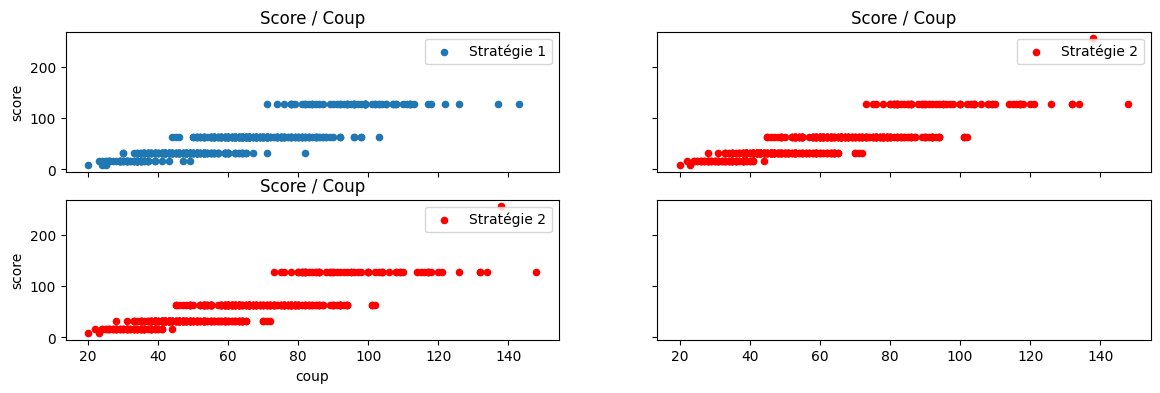
La stratégie 2 paraît meilleure : jouer aléatoire dans toutes les directions est plus efficace que dans deux directions.
[ ]: