Note

Go to the end to download the full example code

Float Conversion#

I came up with the following question (float64)x < (float64)y \Longrightarrow (float32) x < (float32)y? What is the probability this holds?

Probability (float64)x == (float32)x#

Let’s evaluate how many time we draw a random double number equal to its float conversion.

import random
import numpy
import pandas
import matplotlib.pyplot as plt


rnd = numpy.random.random(100000000)
rnd.shape, rnd.dtype

((100000000,), dtype('float64'))

rnd32 = rnd.astype(numpy.float32).astype(numpy.float64)
equal = (rnd == rnd32).sum()
equal

2

It is very low. Let’s check the reverse is true.

rnd32b = rnd32.astype(numpy.float64).astype(numpy.float32)
equal = (rnd32b == rnd32).sum()
equal

100000000

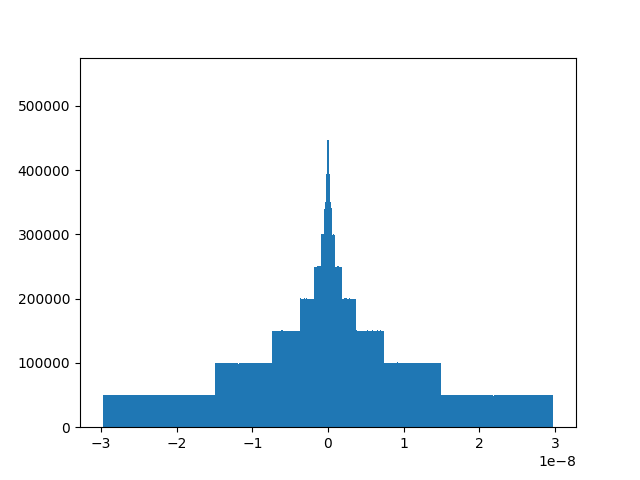
Let’s study the distribution of the difference.

delta = rnd - rnd32
numpy.min(delta), numpy.max(delta)

(-2.980232227667301e-08, 2.9802322387695312e-08)

numpy.min(rnd), numpy.max(rnd)

(1.1707908198488326e-08, 0.999999997344628)

plt.hist(delta, bins=1000)
plot float and double rouding
(array([ 49963.,  50274.,  49885.,  50054.,  49733.,  50129.,  50129.,
        49661.,  50152.,  49916.,  49935.,  49647.,  50099.,  50316.,
        50319.,  49935.,  49975.,  49752.,  49886.,  50382.,  50160.,
        50238.,  50184.,  50064.,  49792.,  49787.,  49753.,  49994.,
        49931.,  49798.,  49841.,  50086.,  50181.,  49978.,  50457.,
        50287.,  49766.,  50253.,  50568.,  49901.,  49840.,  49741.,
        49857.,  49760.,  50226.,  50138.,  50004.,  49938.,  50228.,
        49994.,  50084.,  49850.,  50082.,  49734.,  50238.,  50173.,
        49887.,  49621.,  49718.,  49805.,  50141.,  49961.,  50501.,
        49761.,  50147.,  50197.,  49898.,  50178.,  50288.,  50483.,
        49879.,  49811.,  49906.,  50340.,  49742.,  50052.,  49591.,
        49824.,  49983.,  49990.,  50020.,  50228.,  50390.,  49613.,
        50192.,  50138.,  50216.,  49993.,  50059.,  49688.,  50088.,
        49866.,  49953.,  49624.,  50292.,  50012.,  49604.,  49483.,
        50285.,  49823.,  50489.,  49709.,  49885.,  49928.,  49746.,
        49798.,  50093.,  49853.,  49730.,  49813.,  50102.,  50302.,
        49748.,  50388.,  50152.,  50393.,  49906.,  49655.,  49947.,
        49643.,  49817.,  49908.,  49918.,  49683.,  49782.,  50497.,
        50119.,  49820.,  49987.,  49766.,  50076.,  49816.,  49657.,
        49921.,  49881.,  49648.,  49986.,  49888.,  49905.,  50332.,
        50105.,  50166.,  50245.,  49731.,  50165.,  49809.,  50033.,
        49802.,  50022.,  49839.,  49826.,  50247.,  50104.,  49592.,
        50273.,  50137.,  50227.,  49907.,  50202.,  49952.,  49914.,
        50235.,  50083.,  50450.,  49899.,  50036.,  49758.,  49950.,
        49753.,  49996.,  49790.,  50414.,  50297.,  50022.,  49751.,
        49480.,  49489.,  49785.,  49874.,  49945.,  50043.,  50145.,
        49908.,  49877.,  50278.,  49836.,  49805.,  50107.,  50129.,
        49787.,  50059.,  49948.,  49850.,  49279.,  49904.,  50147.,
        50017.,  50133.,  49863.,  50190.,  50115.,  49939.,  50015.,
        49774.,  50035.,  50379.,  49921.,  50003.,  50016.,  49788.,
        50202.,  50087.,  49708.,  50130.,  49760.,  50260.,  49805.,
        49681.,  49938.,  49662.,  50208.,  49817.,  49763.,  50024.,
        49744.,  49904.,  50044.,  49674.,  49949.,  50261.,  50042.,
        50134.,  49911.,  50275.,  49408.,  50177.,  50261.,  49746.,
        49783.,  49968.,  50222.,  49849.,  50005.,  50396.,  50019.,
        49992.,  50005.,  49840.,  49871.,  50161.,  99841.,  99472.,
        99613.,  99570., 100289., 100046., 100464., 100077.,  99902.,
       100140.,  99892.,  99336., 100654., 100032.,  99882., 100233.,
        99706.,  99981., 100122., 100066., 100084., 100226.,  99957.,
       100230.,  99782.,  99795.,  99914., 100052.,  99722.,  99873.,
        99665., 100297., 100168., 100247., 100509.,  99821., 100015.,
        99970., 100271., 100113.,  99704.,  99924.,  99497.,  99879.,
       100078., 100590., 100155.,  99892., 100030., 100112.,  99917.,
        99124.,  99846.,  99879., 100344., 100118.,  99798., 100236.,
       100274., 100051., 100196., 100043., 100137.,  99984.,  99826.,
        99716.,  99660.,  99822., 100393.,  99941.,  99862., 100641.,
       100233., 100095., 100088.,  99847.,  99798.,  99198.,  99916.,
        99414., 100297., 100164.,  99949., 100233., 100409.,  99758.,
        99420.,  99787.,  99788., 100121.,  99967., 100436.,  99526.,
        99854.,  99776., 100049., 100552., 100275., 100355.,  99847.,
       100448.,  99767.,  99811., 100036.,  99458., 100199.,  99557.,
       100008.,  99978., 100061.,  99920., 100161., 100173.,  99704.,
        99995.,  99802., 100134.,  99884., 100519., 100114., 100338.,
       100384., 100487., 100295., 100353., 149916., 149310., 150333.,
       150416., 149839., 149529., 149478., 149822., 150292., 149622.,
       150233., 149203., 149940., 150204., 149900., 149963., 150287.,
       150257., 150414., 150056., 149964., 151025., 149675., 149890.,
       151035., 150350., 149381., 149941., 150470., 150331., 149950.,
       149953., 150112., 149990., 150477., 150156., 150109., 149977.,
       150421., 149519., 151008., 149814., 149479., 149595., 150369.,
       149581., 150004., 149167., 150247., 150415., 150249., 149402.,
       149923., 149681., 150040., 149639., 149461., 149496., 150013.,
       149688., 150318., 150323., 174958., 200380., 200487., 199979.,
       199974., 200539., 199565., 199848., 199602., 199515., 200357.,
       199935., 200333., 199853., 200144., 200925., 199464., 199975.,
       200546., 200259., 200033., 199956., 200055., 199891., 199670.,
       200423., 199857., 200214., 199431., 199938., 199933., 212276.,
       250392., 249715., 249747., 249827., 250570., 250006., 249926.,
       250680., 250132., 250351., 250300., 250327., 250551., 249389.,
       250261., 280722., 300724., 301269., 300319., 299673., 300174.,
       300393., 300941., 340075., 349606., 350175., 351367., 394785.,
       399463., 446456., 547868., 547248., 447345., 400413., 394336.,
       350453., 350374., 349853., 340744., 299696., 299264., 299623.,
       299284., 300180., 299422., 299690., 281928., 249661., 250987.,
       249624., 249525., 248930., 251016., 250459., 250537., 249421.,
       249530., 249440., 249875., 249011., 249793., 250569., 212539.,
       200256., 200108., 199669., 199862., 200887., 199813., 200385.,
       200691., 200857., 200403., 200283., 199814., 200289., 200272.,
       200454., 200592., 199948., 199647., 199503., 200097., 200132.,
       199746., 199954., 199949., 199618., 200507., 200126., 199233.,
       200287., 199954., 175179., 150726., 149757., 150029., 150176.,
       149998., 150113., 149526., 149565., 149543., 149889., 149088.,
       149663., 149666., 150393., 149490., 150285., 150222., 150432.,
       149297., 150460., 150416., 149597., 150348., 149642., 150655.,
       149900., 149625., 150082., 149435., 149608., 149885., 149998.,
       150333., 149973., 150121., 150509., 149865., 150074., 150354.,
       148577., 149716., 149784., 149172., 150505., 149303., 150089.,
       150644., 150181., 149798., 149730., 150859., 149222., 150063.,
       151217., 150247., 150147., 149463., 150120., 150013., 150357.,
       149538., 150067.,  99795., 100091.,  99883.,  99982., 100185.,
       100085.,  99848., 100011.,  99997.,  99872.,  99794., 100504.,
        99795., 100183., 100429.,  99615.,  99806., 100723., 100085.,
        99747.,  99803., 100030.,  99654.,  99971.,  99572., 100242.,
        99756., 100155.,  99531., 100722.,  99663., 100108., 100049.,
        99875., 100462.,  99437.,  99806.,  99581., 100076.,  99875.,
       100186., 100307., 100105., 100386.,  99829.,  99786.,  99972.,
        99824.,  99875.,  99928.,  99880.,  99724.,  99941.,  99721.,
        99739.,  99821., 100647.,  99951.,  99792.,  99698.,  99975.,
        99938.,  99982., 100140.,  99968.,  99515., 100209.,  99309.,
       100301., 100103.,  99882., 100322., 100108.,  99192., 100235.,
       100017.,  99721.,  99752., 100436.,  99516.,  99919., 100142.,
       100046.,  99732., 100298.,  99714., 100146., 100457., 100696.,
       100055., 100280., 100281.,  99773.,  99778.,  99540., 100063.,
        99904., 100059., 100266.,  99951., 100221.,  99978.,  99878.,
        99400., 100034., 100087.,  99972., 100174., 100088., 100219.,
        99889.,  99893.,  99386.,  99690.,  99665., 100326., 100277.,
       100292.,  99751., 100168.,  99994.,  99798., 100166.,  99851.,
        99774.,  50137.,  50030.,  49828.,  50470.,  49841.,  49443.,
        50134.,  49982.,  50072.,  49996.,  50144.,  49811.,  50031.,
        49959.,  50323.,  49980.,  50105.,  50461.,  49985.,  49985.,
        49872.,  49933.,  50142.,  49749.,  49580.,  50557.,  50000.,
        50610.,  50520.,  49885.,  50052.,  49871.,  49816.,  50295.,
        49949.,  49904.,  49884.,  49977.,  49683.,  49708.,  50317.,
        49928.,  50221.,  49889.,  49543.,  49727.,  50151.,  50036.,
        50334.,  50175.,  50195.,  50283.,  49604.,  50174.,  49802.,
        50026.,  49901.,  50154.,  49849.,  49909.,  49901.,  50026.,
        50127.,  49689.,  49846.,  50121.,  50226.,  50052.,  49808.,
        49990.,  50220.,  49868.,  49654.,  50366.,  50031.,  49733.,
        50075.,  50249.,  49961.,  50086.,  50082.,  49649.,  49867.,
        50177.,  49737.,  50365.,  50071.,  49927.,  49978.,  50030.,
        50320.,  50026.,  50033.,  49960.,  49748.,  49936.,  50247.,
        49874.,  49874.,  50112.,  49780.,  50464.,  49912.,  50093.,
        50179.,  50127.,  49786.,  50417.,  50055.,  49747.,  50115.,
        49728.,  50298.,  49798.,  50309.,  50013.,  49994.,  49142.,
        49869.,  49954.,  50056.,  49913.,  50358.,  49984.,  49997.,
        50187.,  49762.,  50078.,  49994.,  50184.,  50196.,  50015.,
        50055.,  50156.,  49832.,  50362.,  49748.,  49913.,  49960.,
        49653.,  50215.,  50100.,  50243.,  49859.,  50531.,  49872.,
        49935.,  49923.,  50029.,  50236.,  50228.,  49846.,  50275.,
        49796.,  50112.,  50574.,  49842.,  50040.,  49921.,  49746.,
        50188.,  49951.,  50127.,  50119.,  49969.,  49866.,  50145.,
        49509.,  50011.,  49649.,  50354.,  50220.,  50109.,  50242.,
        50096.,  49849.,  49649.,  50086.,  49863.,  50196.,  50014.,
        50177.,  49932.,  50350.,  49979.,  50255.,  49838.,  49891.,
        50185.,  50242.,  50209.,  49747.,  50342.,  49903.,  49981.,
        50138.,  49839.,  49970.,  50096.,  50200.,  50456.,  50094.,
        49865.,  50249.,  50356.,  49937.,  50169.,  50444.,  50173.,
        50308.,  50257.,  49981.,  50033.,  49781.,  50079.,  50047.,
        49641.,  49827.,  50200.,  49515.,  50209.,  50180.,  49897.,
        49626.,  50138.,  49704.,  50222.,  49685.,  49997.,  50093.,
        49989.,  50275.,  49839.,  50154.,  50158.,  49904.,  49797.,
        50131.,  49742.,  50142.,  50181.,  50117.,  50066.,  49936.,
        50296.,  49987.,  50448.,  50043.,  50086.,  50279.]), array([-2.98023223e-08, -2.97427176e-08, -2.96831130e-08, ...,
        2.96831131e-08,  2.97427177e-08,  2.98023224e-08]), <BarContainer object of 1000 artists>)

We finally check that double operations between float numpers remain floats.

for i in range(0, 100000):
    i, j = random.randint(0, len(rnd32) - 1), random.randint(0, len(rnd32) - 1)
    d32 = numpy.float64(rnd32[i] * rnd32[j])
    d64 = numpy.float64(rnd32[i]) * numpy.float64(rnd32[j])
    if d32 != d64:
        raise Exception(
            "Issue with somme={0} = {1} + {2}".format(
                rnd32[i] + rnd32[j], rnd32[i], rnd32[j]
            )
        )

Interval length distribution#

Let’s imagine now we want to define an intervalle in which a double is converted to the same float. Let’s find out about it length.

def find_interval(x):
    dx = numpy.abs(x - numpy.float32(x))  # usually not zero
    dx /= 100
    f = numpy.float32(x)
    x1 = x
    while numpy.float32(x1) == f:
        x1 -= dx
    x2 = x
    while numpy.float32(x2) == f:
        x2 += dx
    return x1 + dx, x2 - dx


length = numpy.zeros((2000,))
for i in range(length.shape[0]):
    x = rnd[i]
    x1, x2 = find_interval(x)
    length[i] = x2 - x1

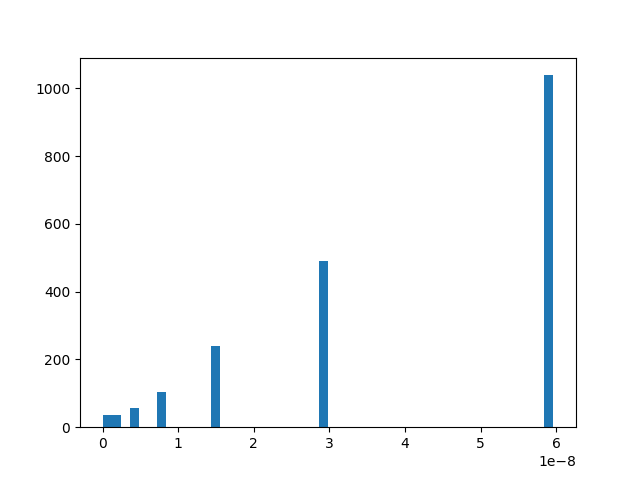
min(length), max(length)

(3.6340828485576307e-12, 5.9604587931971764e-08)

plt.hist(length, bins=50)
plot float and double rouding
(array([  37.,   35.,    0.,   57.,    0.,    0.,  103.,    0.,    0.,
          0.,    0.,    0.,  239.,    0.,    0.,    0.,    0.,    0.,
          0.,    0.,    0.,    0.,    0.,    0.,  490.,    0.,    0.,
          0.,    0.,    0.,    0.,    0.,    0.,    0.,    0.,    0.,
          0.,    0.,    0.,    0.,    0.,    0.,    0.,    0.,    0.,
          0.,    0.,    0.,    0., 1039.]), array([3.63408285e-12, 1.19565316e-09, 2.38767224e-09, 3.57969131e-09,
       4.77171039e-09, 5.96372947e-09, 7.15574854e-09, 8.34776762e-09,
       9.53978670e-09, 1.07318058e-08, 1.19238249e-08, 1.31158439e-08,
       1.43078630e-08, 1.54998821e-08, 1.66919012e-08, 1.78839202e-08,
       1.90759393e-08, 2.02679584e-08, 2.14599775e-08, 2.26519965e-08,
       2.38440156e-08, 2.50360347e-08, 2.62280538e-08, 2.74200729e-08,
       2.86120919e-08, 2.98041110e-08, 3.09961301e-08, 3.21881492e-08,
       3.33801682e-08, 3.45721873e-08, 3.57642064e-08, 3.69562255e-08,
       3.81482445e-08, 3.93402636e-08, 4.05322827e-08, 4.17243018e-08,
       4.29163209e-08, 4.41083399e-08, 4.53003590e-08, 4.64923781e-08,
       4.76843972e-08, 4.88764162e-08, 5.00684353e-08, 5.12604544e-08,
       5.24524735e-08, 5.36444925e-08, 5.48365116e-08, 5.60285307e-08,
       5.72205498e-08, 5.84125689e-08, 5.96045879e-08]), <BarContainer object of 50 artists>)

So we can approximate this interval by something like this:

ql = numpy.sort(length)[int(length.shape[0] * 0.8)]
ql

5.952199622072385e-08

An answer to the initial question#

Let’s estimate \mathbb{P}\left(x_{64} < y_{64} \Longrightarrow x_{32} < y_{32} \; | \; |x-y| \leqslant d\right) ?

def inf_strict(x, y):
    f1 = x < y
    f2 = numpy.float32(x) < numpy.float32(y)
    return f1, f2


def count_events(fct):
    rows = []
    for di in range(1, 1001):
        d = di * ql / 100
        total = 0
        ok = 0
        rnd = numpy.random.random((2000 * 3,))
        for i in range(0, rnd.shape[0], 3):
            s = -1 if rnd[i + 2] < 0.5 else 1
            x, y = rnd[i], rnd[i] + rnd[i + 1] * d * s
            f1, f2 = fct(x, y)
            if f1:
                total += 1
                if f2:
                    ok += 1
        if (di + 10) % 100 == 0:
            print(di, d, ":", ok, total)
        rows.append(dict(d=d, ratio=ok * 1.0 / total, total=total))

    return pandas.DataFrame(rows)


df = count_events(inf_strict)
df.head()

90 5.3569796598651465e-08 : 661 1026
190 1.1309179281937531e-07 : 837 993
290 1.7261378904009916e-07 : 889 1007
390 2.32135785260823e-07 : 923 1016
490 2.9165778148154686e-07 : 942 991
590 3.511797777022707e-07 : 938 987
690 4.1070177392299456e-07 : 929 980
790 4.702237701437184e-07 : 957 999
890 5.297457663644423e-07 : 979 1013
990 5.892677625851661e-07 : 990 1025
d ratio total
0 5.952200e-10 0.028600 1014
1 1.190440e-09 0.033597 1012
2 1.785660e-09 0.047666 1007
3 2.380880e-09 0.059761 1004
4 2.976100e-09 0.070157 955 


df.plot(x="d", y="ratio")
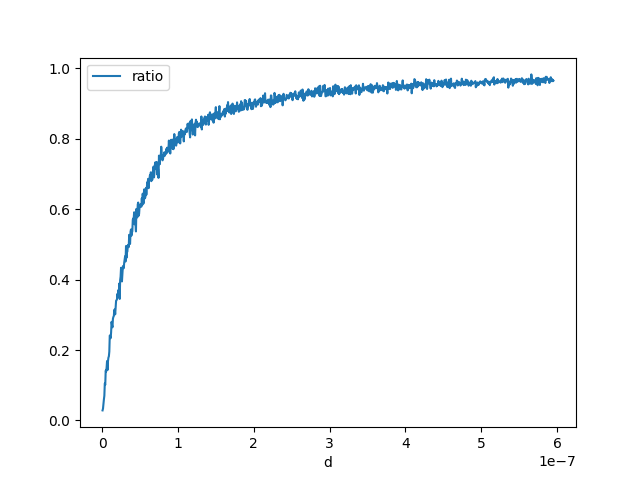
plot float and double rouding
<Axes: xlabel='d'>

df.plot(x="d", y="ratio", logx=True)
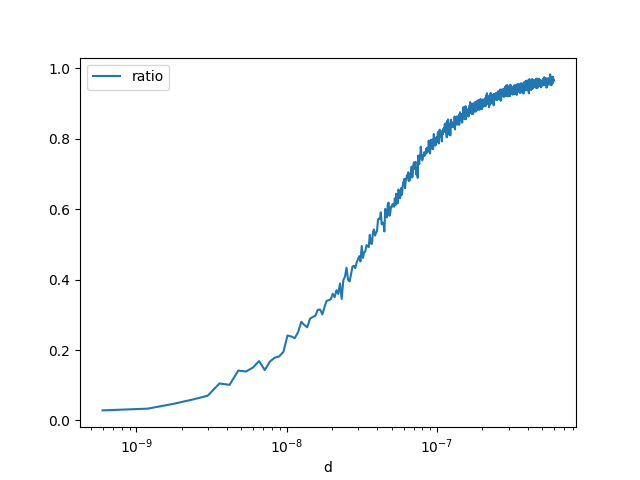
plot float and double rouding
<Axes: xlabel='d'>

An answer to a similar question: what about not strict comparison?#

Let’s estimate \mathbb{P}\left(x_{64} \leqslant y_{64} \Longrightarrow x_{32} \leqslant y_{32} \; | \; |x-y| \leqslant d\right) ?

def inf_equal(x, y):
    f1 = x <= y
    f2 = numpy.float32(x) <= numpy.float32(y)
    return f1, f2


df2 = count_events(inf_equal)
df2.head()

90 5.3569796598651465e-08 : 988 988
190 1.1309179281937531e-07 : 1006 1006
290 1.7261378904009916e-07 : 1012 1012
390 2.32135785260823e-07 : 954 954
490 2.9165778148154686e-07 : 1016 1016
590 3.511797777022707e-07 : 1011 1011
690 4.1070177392299456e-07 : 995 995
790 4.702237701437184e-07 : 1042 1042
890 5.297457663644423e-07 : 1020 1020
990 5.892677625851661e-07 : 994 994
d ratio total
0 5.952200e-10 1.0 994
1 1.190440e-09 1.0 1002
2 1.785660e-09 1.0 1004
3 2.380880e-09 1.0 983
4 2.976100e-09 1.0 995 


ax = df.plot(x="d", y="ratio", logx=True, label="<")
df2.plot(x="d", y="ratio", logx=True, label="<=", ax=ax)
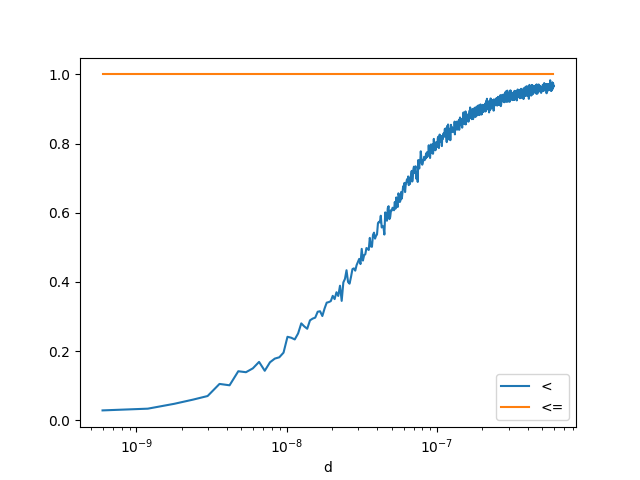
plot float and double rouding
<Axes: xlabel='d'>

def sup_strict(x, y):
    f1 = x > y
    f2 = numpy.float32(x) > numpy.float32(y)
    return f1, f2


df3 = count_events(sup_strict)
df3.head()

90 5.3569796598651465e-08 : 660 998
190 1.1309179281937531e-07 : 789 979
290 1.7261378904009916e-07 : 870 980
390 2.32135785260823e-07 : 925 1011
490 2.9165778148154686e-07 : 895 977
590 3.511797777022707e-07 : 988 1036
690 4.1070177392299456e-07 : 952 999
790 4.702237701437184e-07 : 963 1014
890 5.297457663644423e-07 : 957 993
990 5.892677625851661e-07 : 1002 1034
d ratio total
0 5.952200e-10 0.030542 1015
1 1.190440e-09 0.045862 1003
2 1.785660e-09 0.061825 1019
3 2.380880e-09 0.072614 964
4 2.976100e-09 0.089910 1001 


ax = df.plot(x="d", y="ratio", logx=True, label="<")
df2.plot(x="d", y="ratio", logx=True, label="<=", ax=ax)
df3.plot(x="d", y="ratio", logx=True, label=">", ax=ax)
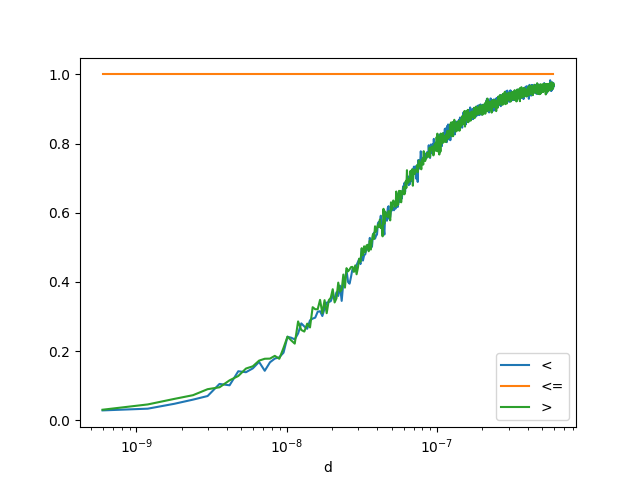
plot float and double rouding
<Axes: xlabel='d'>

def sup_equal(x, y):
    f1 = x >= y
    f2 = numpy.float32(x) >= numpy.float32(y)
    return f1, f2


df4 = count_events(sup_equal)
df4.head()

90 5.3569796598651465e-08 : 1052 1052
190 1.1309179281937531e-07 : 1029 1029
290 1.7261378904009916e-07 : 971 971
390 2.32135785260823e-07 : 988 988
490 2.9165778148154686e-07 : 998 998
590 3.511797777022707e-07 : 977 977
690 4.1070177392299456e-07 : 1006 1006
790 4.702237701437184e-07 : 1031 1031
890 5.297457663644423e-07 : 976 976
990 5.892677625851661e-07 : 984 984
d ratio total
0 5.952200e-10 1.0 1023
1 1.190440e-09 1.0 1002
2 1.785660e-09 1.0 1012
3 2.380880e-09 1.0 981
4 2.976100e-09 1.0 1006 


ax = df.plot(x="d", y="ratio", logx=True, label="<")
df2.plot(x="d", y="ratio", logx=True, label="<=", ax=ax)
df3.plot(x="d", y="ratio", logx=True, label=">", ax=ax)
df4.plot(x="d", y="ratio", logx=True, label=">=", ax=ax)
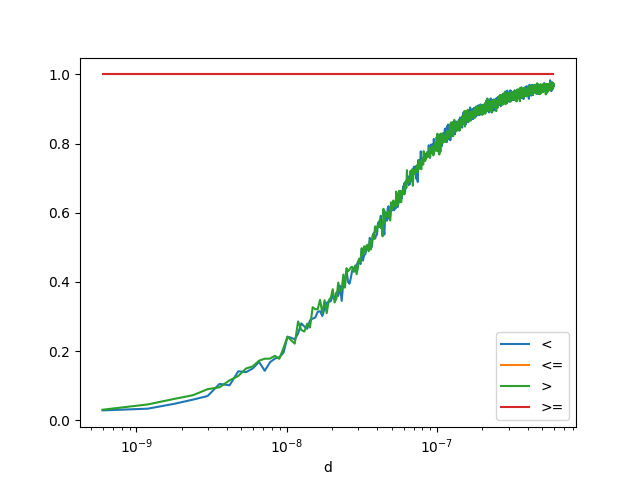
plot float and double rouding
<Axes: xlabel='d'>

def inf_strict_neg(x, y):
    f1 = (-x) >= (-y)
    f2 = (-numpy.float32(x)) >= (-numpy.float32(y))
    return f1, f2


dfn = count_events(inf_strict_neg)
dfn.head()

90 5.3569796598651465e-08 : 982 982
190 1.1309179281937531e-07 : 1006 1006
290 1.7261378904009916e-07 : 970 970
390 2.32135785260823e-07 : 979 979
490 2.9165778148154686e-07 : 988 988
590 3.511797777022707e-07 : 976 976
690 4.1070177392299456e-07 : 1011 1011
790 4.702237701437184e-07 : 953 953
890 5.297457663644423e-07 : 1004 1004
990 5.892677625851661e-07 : 989 989
d ratio total
0 5.952200e-10 1.0 1021
1 1.190440e-09 1.0 1018
2 1.785660e-09 1.0 993
3 2.380880e-09 1.0 1001
4 2.976100e-09 1.0 990 


ax = df.plot(x="d", y="ratio", logx=True, label="<")
dfn.plot(x="d", y="ratio", logx=True, label="-1 x >=", ax=ax)
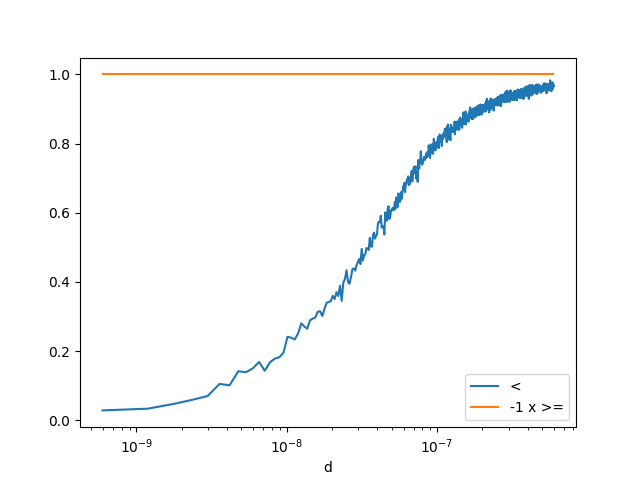
plot float and double rouding
<Axes: xlabel='d'>

Conclusion#

The result is expected. As soon as two float are rounded to the same value, the strict inequality no longer holds. However, if you need to write a code which has to handle double and float (in a template for example), you should use not strict inequalities. It is easier to compare the results but you should read some article like Is < faster than <=?. According to Processing costs of non-strict versus strict comparison, < is 5-10% faster than <=.

Total running time of the script: ( 0 minutes 44.502 seconds)

Gallery generated by Sphinx-Gallery