Note
Go to the end to download the full example code
Custom DecisionTreeRegressor adapted to a linear regression#
A sklearn.tree.DecisionTreeRegressor
can be trained with a couple of possible criterions but it is possible
to implement a custom one (see hellinger_distance_criterion).
See also tutorial
Cython example of exposing C-computed arrays in Python without data copies
which describes a way to implement fast Cython extensions.
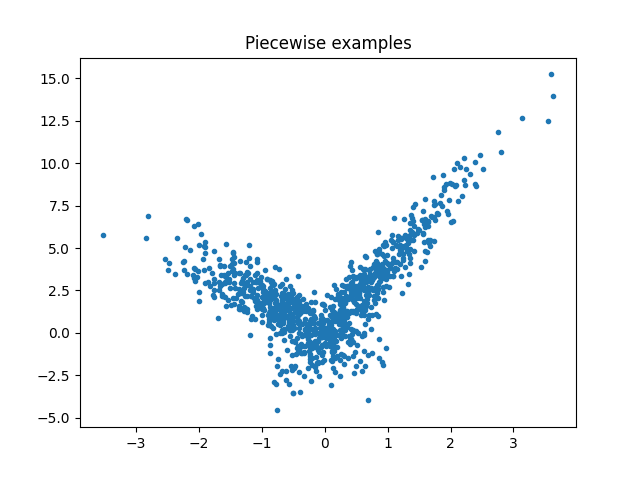
Piecewise data#
Let’s build a toy problem based on two linear models.
import matplotlib.pyplot as plt
import numpy
import numpy.random as npr
from mlinsights.ext_test_case import measure_time
from mlinsights.mlmodel.piecewise_tree_regression import PiecewiseTreeRegressor
from mlinsights.mlmodel.piecewise_tree_regression_criterion import (
SimpleRegressorCriterion,
)
from mlinsights.mlmodel.piecewise_tree_regression_criterion_fast import (
SimpleRegressorCriterionFast,
)
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeRegressor
X = npr.normal(size=(1000, 4))
alpha = [4, -2]
t = (X[:, 0] + X[:, 3] * 0.5) > 0
switch = numpy.zeros(X.shape[0])
switch[t] = 1
y = alpha[0] * X[:, 0] * t + alpha[1] * X[:, 0] * (1 - t) + X[:, 2]
fig, ax = plt.subplots(1, 1)
ax.plot(X[:, 0], y, ".")
ax.set_title("Piecewise examples")
Text(0.5, 1.0, 'Piecewise examples')
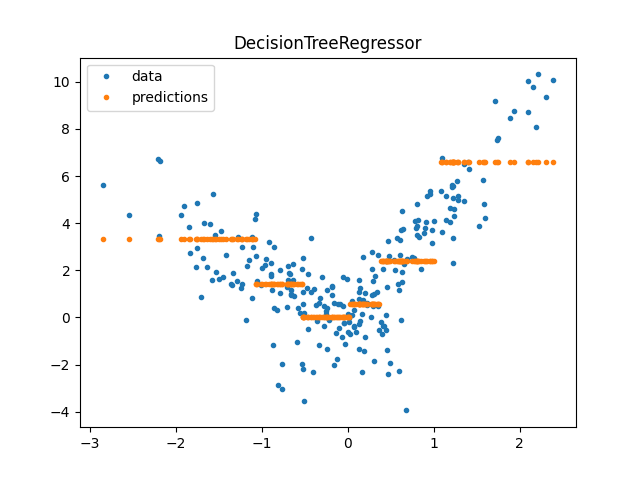
DecisionTreeRegressor#
model = DecisionTreeRegressor(min_samples_leaf=100)
model.fit(X_train, y_train)
pred = model.predict(X_test)
pred[:5]
array([2.40429511, 2.40429511, 0.56609328, 1.40562235, 3.3266729 ])
<matplotlib.legend.Legend object at 0x7fed7bf4c820>
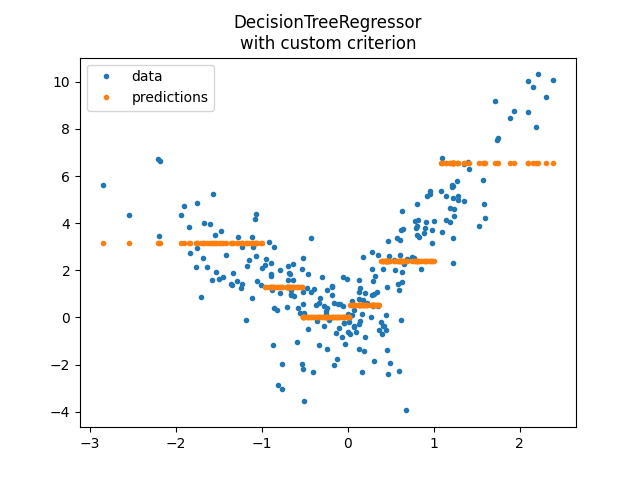
DecisionTreeRegressor with custom implementation#
model2 = DecisionTreeRegressor(
min_samples_leaf=100, criterion=SimpleRegressorCriterion(1, X_train.shape[0])
)
model2.fit(X_train, y_train)
pred = model2.predict(X_test)
pred[:5]
array([2.38186296, 2.38186296, 0.52156596, 3.15224284, 3.15224284])
<matplotlib.legend.Legend object at 0x7fed7bff6e30>
Computation time#
The custom criterion is not really efficient but it was meant that way. The code can be found in piecewise_tree_regression_criterion. Bascially, it is slow because each time the algorithm optimizing the tree needs the class Criterion to evaluate the impurity reduction for a split, the computation happens on the whole data under the node being split. The implementation in _criterion.pyx does it once.
measure_time("model.fit(X_train, y_train)", globals())
{'average': 0.0010175536000024293, 'deviation': 0.0001333961398820299, 'min_exec': 0.0009384960000170395, 'max_exec': 0.0014102120000461583, 'repeat': 10, 'number': 50, 'ttime': 0.010175536000024294, 'context_size': 1176, 'warmup_time': 0.0025584999966667965}
measure_time("model2.fit(X_train, y_train)", globals())
{'average': 0.0037020995999919254, 'deviation': 8.122806822764433e-05, 'min_exec': 0.00358635199998389, 'max_exec': 0.0038612740000826306, 'repeat': 10, 'number': 50, 'ttime': 0.03702099599991925, 'context_size': 1176, 'warmup_time': 0.0037012000029790215}
A loop is involved every time the criterion of the node is involved
which raises a the computation cost of lot. The method _mse
is called each time the algorithm training the decision tree needs
to evaluate a cut, one cut involves elements betwee, position
[start, end[.
ctypedef double float64_t
cdef void _mean(self, SIZE_t start, SIZE_t end, float64_t *mean,
float64_t *weight) nogil:
if start == end:
mean[0] = 0.
return
cdef float64_t m = 0.
cdef float64_t w = 0.
cdef int k
for k in range(start, end):
m += self.sample_wy[k]
w += self.sample_w[k]
weight[0] = w
mean[0] = 0. if w == 0. else m / w
cdef float64_t _mse(self, SIZE_t start, SIZE_t end, float64_t mean,
float64_t weight) nogil:
if start == end:
return 0.
cdef float64_t squ = 0.
cdef int k
for k in range(start, end):
squ += (self.y[self.sample_i[k], 0] - mean) ** 2 * self.sample_w[k]
return 0. if weight == 0. else squ / weight
Better implementation#
I rewrote my first implementation to be closer to what
scikit-learn is doing. The criterion is computed once
for all possible cut and then retrieved on demand.
The code is below, arrays sample_wy_left is the cumulated sum
of starting from the left side
(lower Y). The loop disappeared.
ctypedef double float64_t
cdef void _mean(self, SIZE_t start, SIZE_t end, float64_t *mean,
float64_t *weight) nogil:
if start == end:
mean[0] = 0.
return
cdef float64_t m = self.sample_wy_left[end-1] -
(self.sample_wy_left[start-1] if start > 0 else 0)
cdef float64_t w = self.sample_w_left[end-1] -
(self.sample_w_left[start-1] if start > 0 else 0)
weight[0] = w
mean[0] = 0. if w == 0. else m / w
cdef float64_t _mse(self, SIZE_t start, SIZE_t end, float64_t mean,
float64_t weight) nogil:
if start == end:
return 0.
cdef float64_t squ = self.sample_wy2_left[end-1] -
(self.sample_wy2_left[start-1] if start > 0 else 0)
# This formula only holds if mean is computed on the same interval.
# Otherwise, it is squ / weight - true_mean ** 2 + (mean - true_mean) ** 2.
return 0. if weight == 0. else squ / weight - mean ** 2
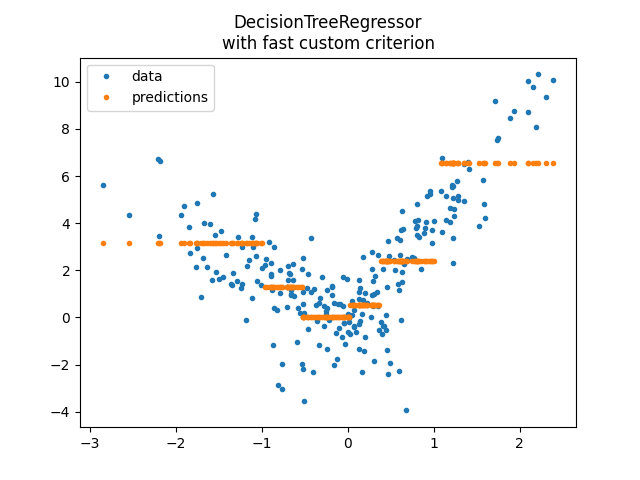
model3 = DecisionTreeRegressor(
min_samples_leaf=100, criterion=SimpleRegressorCriterionFast(1, X_train.shape[0])
)
model3.fit(X_train, y_train)
pred = model3.predict(X_test)
pred[:5]
array([2.38186296, 2.38186296, 0.52156596, 3.15224284, 3.15224284])
<matplotlib.legend.Legend object at 0x7fed7ba9ba60>
measure_time("model3.fit(X_train, y_train)", globals())
{'average': 0.0007811398000194458, 'deviation': 2.59697753379962e-05, 'min_exec': 0.0007485600000654813, 'max_exec': 0.0008361899999727029, 'repeat': 10, 'number': 50, 'ttime': 0.007811398000194458, 'context_size': 1176, 'warmup_time': 0.0011827999987872317}
Much better even though this implementation is currently 3, 4 times slower than scikit-learn’s. Let’s check with a datasets three times bigger to see if it is a fix cost or a cost.
X_train3 = numpy.vstack([X_train, X_train, X_train])
y_train3 = numpy.hstack([y_train, y_train, y_train])
((750, 1), (2250, 1), (2250,))
measure_time("model.fit(X_train3, y_train3)", globals())
{'average': 0.0018330712000170022, 'deviation': 2.8489666644657162e-05, 'min_exec': 0.0017816940000921022, 'max_exec': 0.0018643219998921267, 'repeat': 10, 'number': 50, 'ttime': 0.018330712000170023, 'context_size': 1176, 'warmup_time': 0.0020377999971969984}
The criterion needs to be reinstanciated since it depends on the features X. The computation does not but the design does. This was introduced to compare the current output with a decision tree optimizing for a piecewise linear regression and not a stepwise regression.
try:
model3.fit(X_train3, y_train3)
except Exception as e:
print(e)
n_samples=750 -- y.shape=[2250, 1, 0, 0, 0, 0, 0, 0]
model3 = DecisionTreeRegressor(
min_samples_leaf=100, criterion=SimpleRegressorCriterionFast(1, X_train3.shape[0])
)
measure_time("model3.fit(X_train3, y_train3)", globals())
{'average': 0.001487626200017985, 'deviation': 1.773119843468544e-05, 'min_exec': 0.0014684660000784788, 'max_exec': 0.0015218340000137686, 'repeat': 10, 'number': 50, 'ttime': 0.01487626200017985, 'context_size': 1176, 'warmup_time': 0.0015787000011187047}
Still almost 2 times slower but of the same order of magnitude. We could go further and investigate why or continue and introduce a criterion which optimizes a piecewise linear regression instead of a stepwise regression.
Criterion adapted for a linear regression#
The previous examples are all about decision trees which approximates a
function by a stepwise function. On every interval ,
the model optimizes
and finds the best constant (= the average)
approxmating the function on this interval.
We would to like to approximate the function by a regression line and not a
constant anymore. It means minimizing
.
Doing this require to change the criterion used to split the space of feature
into buckets and the prediction function of the decision tree which now
needs to return a dot product.
fixed = False
if fixed:
# It does not work yet.
piece = PiecewiseTreeRegressor(criterion="mselin", min_samples_leaf=100)
piece.fit(X_train, y_train)
The coefficients for the linear regressions are kept into the following attribute:
if fixed:
piece.betas_
Mapped to the following leaves:
if fixed:
piece.leaves_index_, piece.leaves_mapping_
We can get the leave each observation falls into:
The training is quite slow as it is training many linear regressions each time a split is evaluated.
if fixed:
measure_time("piece.fit(X_train, y_train)", globals())
if fixed:
measure_time("piece.fit(X_train3, y_train3)", globals())
It works but it is slow, slower than the slow implementation of the standard criterion for decision tree regression.
Next#
PR Model trees (M5P and co) and issue Model trees (M5P) propose an implementation a piecewise regression with any kind of regression model. It is based on Building Model Trees. It fits many models to find the best splits and should be slower than this implementation in the case of a decision tree regressor associated with linear regressions.
Total running time of the script: (0 minutes 4.769 seconds)