Benchmark of TreeEnsemble implementation¶

The following example compares the inference time between onnxruntime and sklearn.ensemble.RandomForestRegressor, fow different number of estimators, max depth, and parallelization. It does it for a fixed number of rows and features.

import and registration of necessary converters¶

import pickle
import os
import time
from itertools import product

import matplotlib.pyplot as plt
import numpy
import pandas
from lightgbm import LGBMRegressor
from onnxruntime import InferenceSession, SessionOptions
from psutil import cpu_count
from sphinx_runpython.runpython import run_cmd
from skl2onnx import to_onnx, update_registered_converter
from skl2onnx.common.shape_calculator import calculate_linear_regressor_output_shapes
from sklearn import set_config
from sklearn.ensemble import RandomForestRegressor
from tqdm import tqdm
from xgboost import XGBRegressor
from onnxmltools.convert.xgboost.operator_converters.XGBoost import convert_xgboost


def skl2onnx_convert_lightgbm(scope, operator, container):
    from onnxmltools.convert.lightgbm.operator_converters.LightGbm import (
        convert_lightgbm,
    )

    options = scope.get_options(operator.raw_operator)
    operator.split = options.get("split", None)
    convert_lightgbm(scope, operator, container)


update_registered_converter(
    LGBMRegressor,
    "LightGbmLGBMRegressor",
    calculate_linear_regressor_output_shapes,
    skl2onnx_convert_lightgbm,
    options={"split": None},
)
update_registered_converter(
    XGBRegressor,
    "XGBoostXGBRegressor",
    calculate_linear_regressor_output_shapes,
    convert_xgboost,
)

# The following instruction reduces the time spent by scikit-learn
# to validate the data.
set_config(assume_finite=True)

Machine details¶

print(f"Number of cores: {cpu_count()}")

Number of cores: 20

But this information is not usually enough. Let’s extract the cache information.

try:
    out, err = run_cmd("lscpu")
    print(out)
except Exception as e:
    print(f"lscpu not available: {e}")

<Popen: returncode: None args: ['lscpu']>

Or with the following command.

out, err = run_cmd("cat /proc/cpuinfo")
print(out)

<Popen: returncode: None args: ['cat', '/proc/cpuinfo']>

Fonction to measure inference time¶

def measure_inference(fct, X, repeat, max_time=5, quantile=1):
    """
    Run *repeat* times the same function on data *X*.

    :param fct: fonction to run
    :param X: data
    :param repeat: number of times to run
    :param max_time: maximum time to use to measure the inference
    :return: number of runs, sum of the time, average, median
    """
    times = []
    for _n in range(repeat):
        perf = time.perf_counter()
        fct(X)
        delta = time.perf_counter() - perf
        times.append(delta)
        if len(times) < 3:
            continue
        if max_time is not None and sum(times) >= max_time:
            break
    times.sort()
    quantile = 0 if (len(times) - quantile * 2) < 3 else quantile
    if quantile == 0:
        tt = times
    else:
        tt = times[quantile:-quantile]
    return (len(times), sum(times), sum(tt) / len(tt), times[len(times) // 2])

Benchmark¶

The following script benchmarks the inference for the same model for a random forest and onnxruntime after it was converted into ONNX and for the following configurations.

small = cpu_count() < 25
if small:
    N = 1000
    n_features = 10
    n_jobs = [1, cpu_count() // 2, cpu_count()]
    n_ests = [10, 20, 30]
    depth = [4, 6, 8, 10]
    Regressor = RandomForestRegressor
else:
    N = 100000
    n_features = 50
    n_jobs = [cpu_count(), cpu_count() // 2, 1]
    n_ests = [100, 200, 400]
    depth = [6, 8, 10, 12, 14]
    Regressor = RandomForestRegressor

legend = f"parallel-nf-{n_features}-"

# avoid duplicates on machine with 1 or 2 cores.
n_jobs = list(sorted(set(n_jobs), reverse=True))

Benchmark parameters

repeat = 7  # repeat n times the same inference
quantile = 1  # exclude extreme times
max_time = 5  # maximum number of seconds to spend on one configuration

Data

X = numpy.random.randn(N, n_features).astype(numpy.float32)
noise = (numpy.random.randn(X.shape[0]) / (n_features // 5)).astype(numpy.float32)
y = X.mean(axis=1) + noise
n_train = min(N, N // 3)


data = []
couples = list(product(n_jobs, depth, n_ests))
bar = tqdm(couples)
cache_dir = "_cache"
if not os.path.exists(cache_dir):
    os.mkdir(cache_dir)

for n_j, max_depth, n_estimators in bar:
    if n_j == 1 and n_estimators > n_ests[0]:
        # skipping
        continue

    # parallelization
    cache_name = os.path.join(
        cache_dir, f"nf-{X.shape[1]}-rf-J-{n_j}-E-{n_estimators}-D-{max_depth}.pkl"
    )
    if os.path.exists(cache_name):
        with open(cache_name, "rb") as f:
            rf = pickle.load(f)
    else:
        bar.set_description(f"J={n_j} E={n_estimators} D={max_depth} train rf")
        if n_j == 1 and issubclass(Regressor, RandomForestRegressor):
            rf = Regressor(max_depth=max_depth, n_estimators=n_estimators, n_jobs=-1)
            rf.fit(X[:n_train], y[:n_train])
            rf.n_jobs = 1
        else:
            rf = Regressor(max_depth=max_depth, n_estimators=n_estimators, n_jobs=n_j)
            rf.fit(X[:n_train], y[:n_train])
        with open(cache_name, "wb") as f:
            pickle.dump(rf, f)

    bar.set_description(f"J={n_j} E={n_estimators} D={max_depth} ISession")
    so = SessionOptions()
    so.intra_op_num_threads = n_j
    cache_name = os.path.join(
        cache_dir, f"nf-{X.shape[1]}-rf-J-{n_j}-E-{n_estimators}-D-{max_depth}.onnx"
    )
    if os.path.exists(cache_name):
        sess = InferenceSession(cache_name, so, providers=["CPUExecutionProvider"])
    else:
        bar.set_description(f"J={n_j} E={n_estimators} D={max_depth} cvt onnx")
        onx = to_onnx(rf, X[:1])
        with open(cache_name, "wb") as f:
            f.write(onx.SerializeToString())
        sess = InferenceSession(cache_name, so, providers=["CPUExecutionProvider"])
    onx_size = os.stat(cache_name).st_size

    # run once to avoid counting the first run
    bar.set_description(f"J={n_j} E={n_estimators} D={max_depth} predict1")
    rf.predict(X)
    sess.run(None, {"X": X})

    # fixed data
    obs = dict(
        n_jobs=n_j,
        max_depth=max_depth,
        n_estimators=n_estimators,
        repeat=repeat,
        max_time=max_time,
        name=rf.__class__.__name__,
        n_rows=X.shape[0],
        n_features=X.shape[1],
        onnx_size=onx_size,
    )

    # baseline
    bar.set_description(f"J={n_j} E={n_estimators} D={max_depth} predictB")
    r, t, mean, med = measure_inference(rf.predict, X, repeat=repeat, max_time=max_time)
    o1 = obs.copy()
    o1.update(dict(avg=mean, med=med, n_runs=r, ttime=t, name="base"))
    data.append(o1)

    # onnxruntime
    bar.set_description(f"J={n_j} E={n_estimators} D={max_depth} predictO")
    r, t, mean, med = measure_inference(
        lambda x, sess=sess: sess.run(None, {"X": x}),
        X,
        repeat=repeat,
        max_time=max_time,
    )
    o2 = obs.copy()
    o2.update(dict(avg=mean, med=med, n_runs=r, ttime=t, name="ort_"))
    data.append(o2)

  0%|          | 0/36 [00:00<?, ?it/s]
J=20 E=10 D=4 train rf:   0%|          | 0/36 [00:00<?, ?it/s]
J=20 E=10 D=4 ISession:   0%|          | 0/36 [00:00<?, ?it/s]
J=20 E=10 D=4 cvt onnx:   0%|          | 0/36 [00:00<?, ?it/s]
J=20 E=10 D=4 predict1:   0%|          | 0/36 [00:00<?, ?it/s]
J=20 E=10 D=4 predictB:   0%|          | 0/36 [00:00<?, ?it/s]
J=20 E=10 D=4 predictO:   0%|          | 0/36 [00:00<?, ?it/s]
J=20 E=10 D=4 predictO:   3%|▎         | 1/36 [00:00<00:16,  2.12it/s]
J=20 E=20 D=4 train rf:   3%|▎         | 1/36 [00:00<00:16,  2.12it/s]
J=20 E=20 D=4 ISession:   3%|▎         | 1/36 [00:00<00:16,  2.12it/s]
J=20 E=20 D=4 cvt onnx:   3%|▎         | 1/36 [00:00<00:16,  2.12it/s]
J=20 E=20 D=4 predict1:   3%|▎         | 1/36 [00:00<00:16,  2.12it/s]
J=20 E=20 D=4 predictB:   3%|▎         | 1/36 [00:00<00:16,  2.12it/s]
J=20 E=20 D=4 predictO:   3%|▎         | 1/36 [00:00<00:16,  2.12it/s]
J=20 E=20 D=4 predictO:   6%|▌         | 2/36 [00:00<00:17,  2.00it/s]
J=20 E=30 D=4 train rf:   6%|▌         | 2/36 [00:00<00:17,  2.00it/s]
J=20 E=30 D=4 ISession:   6%|▌         | 2/36 [00:01<00:17,  2.00it/s]
J=20 E=30 D=4 cvt onnx:   6%|▌         | 2/36 [00:01<00:17,  2.00it/s]
J=20 E=30 D=4 predict1:   6%|▌         | 2/36 [00:01<00:17,  2.00it/s]
J=20 E=30 D=4 predictB:   6%|▌         | 2/36 [00:01<00:17,  2.00it/s]
J=20 E=30 D=4 predictO:   6%|▌         | 2/36 [00:01<00:17,  2.00it/s]
J=20 E=30 D=4 predictO:   8%|▊         | 3/36 [00:01<00:14,  2.20it/s]
J=20 E=10 D=6 train rf:   8%|▊         | 3/36 [00:01<00:14,  2.20it/s]
J=20 E=10 D=6 ISession:   8%|▊         | 3/36 [00:01<00:14,  2.20it/s]
J=20 E=10 D=6 cvt onnx:   8%|▊         | 3/36 [00:01<00:14,  2.20it/s]
J=20 E=10 D=6 predict1:   8%|▊         | 3/36 [00:01<00:14,  2.20it/s]
J=20 E=10 D=6 predictB:   8%|▊         | 3/36 [00:01<00:14,  2.20it/s]
J=20 E=10 D=6 predictO:   8%|▊         | 3/36 [00:01<00:14,  2.20it/s]
J=20 E=10 D=6 predictO:  11%|█         | 4/36 [00:01<00:12,  2.51it/s]
J=20 E=20 D=6 train rf:  11%|█         | 4/36 [00:01<00:12,  2.51it/s]
J=20 E=20 D=6 ISession:  11%|█         | 4/36 [00:01<00:12,  2.51it/s]
J=20 E=20 D=6 cvt onnx:  11%|█         | 4/36 [00:01<00:12,  2.51it/s]
J=20 E=20 D=6 predict1:  11%|█         | 4/36 [00:01<00:12,  2.51it/s]
J=20 E=20 D=6 predictB:  11%|█         | 4/36 [00:01<00:12,  2.51it/s]
J=20 E=20 D=6 predictO:  11%|█         | 4/36 [00:01<00:12,  2.51it/s]
J=20 E=20 D=6 predictO:  14%|█▍        | 5/36 [00:01<00:11,  2.77it/s]
J=20 E=30 D=6 train rf:  14%|█▍        | 5/36 [00:01<00:11,  2.77it/s]
J=20 E=30 D=6 ISession:  14%|█▍        | 5/36 [00:02<00:11,  2.77it/s]
J=20 E=30 D=6 cvt onnx:  14%|█▍        | 5/36 [00:02<00:11,  2.77it/s]
J=20 E=30 D=6 predict1:  14%|█▍        | 5/36 [00:02<00:11,  2.77it/s]
J=20 E=30 D=6 predictB:  14%|█▍        | 5/36 [00:02<00:11,  2.77it/s]
J=20 E=30 D=6 predictO:  14%|█▍        | 5/36 [00:02<00:11,  2.77it/s]
J=20 E=30 D=6 predictO:  17%|█▋        | 6/36 [00:02<00:11,  2.72it/s]
J=20 E=10 D=8 train rf:  17%|█▋        | 6/36 [00:02<00:11,  2.72it/s]
J=20 E=10 D=8 ISession:  17%|█▋        | 6/36 [00:02<00:11,  2.72it/s]
J=20 E=10 D=8 cvt onnx:  17%|█▋        | 6/36 [00:02<00:11,  2.72it/s]
J=20 E=10 D=8 predict1:  17%|█▋        | 6/36 [00:02<00:11,  2.72it/s]
J=20 E=10 D=8 predictB:  17%|█▋        | 6/36 [00:02<00:11,  2.72it/s]
J=20 E=10 D=8 predictO:  17%|█▋        | 6/36 [00:02<00:11,  2.72it/s]
J=20 E=10 D=8 predictO:  19%|█▉        | 7/36 [00:02<00:10,  2.80it/s]
J=20 E=20 D=8 train rf:  19%|█▉        | 7/36 [00:02<00:10,  2.80it/s]
J=20 E=20 D=8 ISession:  19%|█▉        | 7/36 [00:02<00:10,  2.80it/s]
J=20 E=20 D=8 cvt onnx:  19%|█▉        | 7/36 [00:02<00:10,  2.80it/s]
J=20 E=20 D=8 predict1:  19%|█▉        | 7/36 [00:02<00:10,  2.80it/s]
J=20 E=20 D=8 predictB:  19%|█▉        | 7/36 [00:02<00:10,  2.80it/s]
J=20 E=20 D=8 predictO:  19%|█▉        | 7/36 [00:03<00:10,  2.80it/s]
J=20 E=20 D=8 predictO:  22%|██▏       | 8/36 [00:03<00:10,  2.65it/s]
J=20 E=30 D=8 train rf:  22%|██▏       | 8/36 [00:03<00:10,  2.65it/s]
J=20 E=30 D=8 ISession:  22%|██▏       | 8/36 [00:03<00:10,  2.65it/s]
J=20 E=30 D=8 cvt onnx:  22%|██▏       | 8/36 [00:03<00:10,  2.65it/s]
J=20 E=30 D=8 predict1:  22%|██▏       | 8/36 [00:03<00:10,  2.65it/s]
J=20 E=30 D=8 predictB:  22%|██▏       | 8/36 [00:03<00:10,  2.65it/s]
J=20 E=30 D=8 predictO:  22%|██▏       | 8/36 [00:03<00:10,  2.65it/s]
J=20 E=30 D=8 predictO:  25%|██▌       | 9/36 [00:03<00:11,  2.32it/s]
J=20 E=10 D=10 train rf:  25%|██▌       | 9/36 [00:03<00:11,  2.32it/s]
J=20 E=10 D=10 ISession:  25%|██▌       | 9/36 [00:03<00:11,  2.32it/s]
J=20 E=10 D=10 cvt onnx:  25%|██▌       | 9/36 [00:03<00:11,  2.32it/s]
J=20 E=10 D=10 predict1:  25%|██▌       | 9/36 [00:05<00:11,  2.32it/s]
J=20 E=10 D=10 predictB:  25%|██▌       | 9/36 [00:05<00:11,  2.32it/s]
J=20 E=10 D=10 predictO:  25%|██▌       | 9/36 [00:05<00:11,  2.32it/s]
J=20 E=10 D=10 predictO:  28%|██▊       | 10/36 [00:05<00:20,  1.24it/s]
J=20 E=20 D=10 train rf:  28%|██▊       | 10/36 [00:05<00:20,  1.24it/s]
J=20 E=20 D=10 ISession:  28%|██▊       | 10/36 [00:05<00:20,  1.24it/s]
J=20 E=20 D=10 cvt onnx:  28%|██▊       | 10/36 [00:05<00:20,  1.24it/s]
J=20 E=20 D=10 predict1:  28%|██▊       | 10/36 [00:05<00:20,  1.24it/s]
J=20 E=20 D=10 predictB:  28%|██▊       | 10/36 [00:05<00:20,  1.24it/s]
J=20 E=20 D=10 predictO:  28%|██▊       | 10/36 [00:05<00:20,  1.24it/s]
J=20 E=20 D=10 predictO:  31%|███       | 11/36 [00:05<00:18,  1.34it/s]
J=20 E=30 D=10 train rf:  31%|███       | 11/36 [00:05<00:18,  1.34it/s]
J=20 E=30 D=10 ISession:  31%|███       | 11/36 [00:06<00:18,  1.34it/s]
J=20 E=30 D=10 cvt onnx:  31%|███       | 11/36 [00:06<00:18,  1.34it/s]
J=20 E=30 D=10 predict1:  31%|███       | 11/36 [00:06<00:18,  1.34it/s]
J=20 E=30 D=10 predictB:  31%|███       | 11/36 [00:06<00:18,  1.34it/s]
J=20 E=30 D=10 predictO:  31%|███       | 11/36 [00:06<00:18,  1.34it/s]
J=20 E=30 D=10 predictO:  33%|███▎      | 12/36 [00:06<00:16,  1.46it/s]
J=10 E=10 D=4 train rf:  33%|███▎      | 12/36 [00:06<00:16,  1.46it/s]
J=10 E=10 D=4 ISession:  33%|███▎      | 12/36 [00:06<00:16,  1.46it/s]
J=10 E=10 D=4 cvt onnx:  33%|███▎      | 12/36 [00:06<00:16,  1.46it/s]
J=10 E=10 D=4 predict1:  33%|███▎      | 12/36 [00:06<00:16,  1.46it/s]
J=10 E=10 D=4 predictB:  33%|███▎      | 12/36 [00:06<00:16,  1.46it/s]
J=10 E=10 D=4 predictO:  33%|███▎      | 12/36 [00:06<00:16,  1.46it/s]
J=10 E=10 D=4 predictO:  36%|███▌      | 13/36 [00:06<00:12,  1.85it/s]
J=10 E=20 D=4 train rf:  36%|███▌      | 13/36 [00:06<00:12,  1.85it/s]
J=10 E=20 D=4 ISession:  36%|███▌      | 13/36 [00:06<00:12,  1.85it/s]
J=10 E=20 D=4 cvt onnx:  36%|███▌      | 13/36 [00:06<00:12,  1.85it/s]
J=10 E=20 D=4 predict1:  36%|███▌      | 13/36 [00:06<00:12,  1.85it/s]
J=10 E=20 D=4 predictB:  36%|███▌      | 13/36 [00:06<00:12,  1.85it/s]
J=10 E=20 D=4 predictO:  36%|███▌      | 13/36 [00:06<00:12,  1.85it/s]
J=10 E=20 D=4 predictO:  39%|███▉      | 14/36 [00:06<00:09,  2.28it/s]
J=10 E=30 D=4 train rf:  39%|███▉      | 14/36 [00:06<00:09,  2.28it/s]
J=10 E=30 D=4 ISession:  39%|███▉      | 14/36 [00:06<00:09,  2.28it/s]
J=10 E=30 D=4 cvt onnx:  39%|███▉      | 14/36 [00:06<00:09,  2.28it/s]
J=10 E=30 D=4 predict1:  39%|███▉      | 14/36 [00:06<00:09,  2.28it/s]
J=10 E=30 D=4 predictB:  39%|███▉      | 14/36 [00:07<00:09,  2.28it/s]
J=10 E=30 D=4 predictO:  39%|███▉      | 14/36 [00:07<00:09,  2.28it/s]
J=10 E=30 D=4 predictO:  42%|████▏     | 15/36 [00:07<00:08,  2.47it/s]
J=10 E=10 D=6 train rf:  42%|████▏     | 15/36 [00:07<00:08,  2.47it/s]
J=10 E=10 D=6 ISession:  42%|████▏     | 15/36 [00:07<00:08,  2.47it/s]
J=10 E=10 D=6 cvt onnx:  42%|████▏     | 15/36 [00:07<00:08,  2.47it/s]
J=10 E=10 D=6 predict1:  42%|████▏     | 15/36 [00:07<00:08,  2.47it/s]
J=10 E=10 D=6 predictB:  42%|████▏     | 15/36 [00:07<00:08,  2.47it/s]
J=10 E=10 D=6 predictO:  42%|████▏     | 15/36 [00:07<00:08,  2.47it/s]
J=10 E=10 D=6 predictO:  44%|████▍     | 16/36 [00:07<00:06,  2.96it/s]
J=10 E=20 D=6 train rf:  44%|████▍     | 16/36 [00:07<00:06,  2.96it/s]
J=10 E=20 D=6 ISession:  44%|████▍     | 16/36 [00:07<00:06,  2.96it/s]
J=10 E=20 D=6 cvt onnx:  44%|████▍     | 16/36 [00:07<00:06,  2.96it/s]
J=10 E=20 D=6 predict1:  44%|████▍     | 16/36 [00:07<00:06,  2.96it/s]
J=10 E=20 D=6 predictB:  44%|████▍     | 16/36 [00:07<00:06,  2.96it/s]
J=10 E=20 D=6 predictO:  44%|████▍     | 16/36 [00:07<00:06,  2.96it/s]
J=10 E=20 D=6 predictO:  47%|████▋     | 17/36 [00:07<00:05,  3.18it/s]
J=10 E=30 D=6 train rf:  47%|████▋     | 17/36 [00:07<00:05,  3.18it/s]
J=10 E=30 D=6 ISession:  47%|████▋     | 17/36 [00:07<00:05,  3.18it/s]
J=10 E=30 D=6 cvt onnx:  47%|████▋     | 17/36 [00:07<00:05,  3.18it/s]
J=10 E=30 D=6 predict1:  47%|████▋     | 17/36 [00:07<00:05,  3.18it/s]
J=10 E=30 D=6 predictB:  47%|████▋     | 17/36 [00:07<00:05,  3.18it/s]
J=10 E=30 D=6 predictO:  47%|████▋     | 17/36 [00:08<00:05,  3.18it/s]
J=10 E=30 D=6 predictO:  50%|█████     | 18/36 [00:08<00:05,  3.08it/s]
J=10 E=10 D=8 train rf:  50%|█████     | 18/36 [00:08<00:05,  3.08it/s]
J=10 E=10 D=8 ISession:  50%|█████     | 18/36 [00:08<00:05,  3.08it/s]
J=10 E=10 D=8 cvt onnx:  50%|█████     | 18/36 [00:08<00:05,  3.08it/s]
J=10 E=10 D=8 predict1:  50%|█████     | 18/36 [00:08<00:05,  3.08it/s]
J=10 E=10 D=8 predictB:  50%|█████     | 18/36 [00:08<00:05,  3.08it/s]
J=10 E=10 D=8 predictO:  50%|█████     | 18/36 [00:08<00:05,  3.08it/s]
J=10 E=10 D=8 predictO:  53%|█████▎    | 19/36 [00:08<00:04,  3.50it/s]
J=10 E=20 D=8 train rf:  53%|█████▎    | 19/36 [00:08<00:04,  3.50it/s]
J=10 E=20 D=8 ISession:  53%|█████▎    | 19/36 [00:08<00:04,  3.50it/s]
J=10 E=20 D=8 cvt onnx:  53%|█████▎    | 19/36 [00:08<00:04,  3.50it/s]
J=10 E=20 D=8 predict1:  53%|█████▎    | 19/36 [00:08<00:04,  3.50it/s]
J=10 E=20 D=8 predictB:  53%|█████▎    | 19/36 [00:08<00:04,  3.50it/s]
J=10 E=20 D=8 predictO:  53%|█████▎    | 19/36 [00:08<00:04,  3.50it/s]
J=10 E=20 D=8 predictO:  56%|█████▌    | 20/36 [00:08<00:04,  3.57it/s]
J=10 E=30 D=8 train rf:  56%|█████▌    | 20/36 [00:08<00:04,  3.57it/s]
J=10 E=30 D=8 ISession:  56%|█████▌    | 20/36 [00:08<00:04,  3.57it/s]
J=10 E=30 D=8 cvt onnx:  56%|█████▌    | 20/36 [00:08<00:04,  3.57it/s]
J=10 E=30 D=8 predict1:  56%|█████▌    | 20/36 [00:08<00:04,  3.57it/s]
J=10 E=30 D=8 predictB:  56%|█████▌    | 20/36 [00:08<00:04,  3.57it/s]
J=10 E=30 D=8 predictO:  56%|█████▌    | 20/36 [00:08<00:04,  3.57it/s]
J=10 E=30 D=8 predictO:  58%|█████▊    | 21/36 [00:08<00:04,  3.36it/s]
J=10 E=10 D=10 train rf:  58%|█████▊    | 21/36 [00:08<00:04,  3.36it/s]
J=10 E=10 D=10 ISession:  58%|█████▊    | 21/36 [00:08<00:04,  3.36it/s]
J=10 E=10 D=10 cvt onnx:  58%|█████▊    | 21/36 [00:08<00:04,  3.36it/s]
J=10 E=10 D=10 predict1:  58%|█████▊    | 21/36 [00:08<00:04,  3.36it/s]
J=10 E=10 D=10 predictB:  58%|█████▊    | 21/36 [00:08<00:04,  3.36it/s]
J=10 E=10 D=10 predictO:  58%|█████▊    | 21/36 [00:09<00:04,  3.36it/s]
J=10 E=10 D=10 predictO:  61%|██████    | 22/36 [00:09<00:03,  3.69it/s]
J=10 E=20 D=10 train rf:  61%|██████    | 22/36 [00:09<00:03,  3.69it/s]
J=10 E=20 D=10 ISession:  61%|██████    | 22/36 [00:09<00:03,  3.69it/s]
J=10 E=20 D=10 cvt onnx:  61%|██████    | 22/36 [00:09<00:03,  3.69it/s]
J=10 E=20 D=10 predict1:  61%|██████    | 22/36 [00:09<00:03,  3.69it/s]
J=10 E=20 D=10 predictB:  61%|██████    | 22/36 [00:09<00:03,  3.69it/s]
J=10 E=20 D=10 predictO:  61%|██████    | 22/36 [00:09<00:03,  3.69it/s]
J=10 E=20 D=10 predictO:  64%|██████▍   | 23/36 [00:09<00:03,  3.85it/s]
J=10 E=30 D=10 train rf:  64%|██████▍   | 23/36 [00:09<00:03,  3.85it/s]
J=10 E=30 D=10 ISession:  64%|██████▍   | 23/36 [00:09<00:03,  3.85it/s]
J=10 E=30 D=10 cvt onnx:  64%|██████▍   | 23/36 [00:09<00:03,  3.85it/s]
J=10 E=30 D=10 predict1:  64%|██████▍   | 23/36 [00:09<00:03,  3.85it/s]
J=10 E=30 D=10 predictB:  64%|██████▍   | 23/36 [00:09<00:03,  3.85it/s]
J=10 E=30 D=10 predictO:  64%|██████▍   | 23/36 [00:09<00:03,  3.85it/s]
J=10 E=30 D=10 predictO:  67%|██████▋   | 24/36 [00:09<00:03,  3.43it/s]
J=1 E=10 D=4 train rf:  67%|██████▋   | 24/36 [00:09<00:03,  3.43it/s]
J=1 E=10 D=4 ISession:  67%|██████▋   | 24/36 [00:09<00:03,  3.43it/s]
J=1 E=10 D=4 cvt onnx:  67%|██████▋   | 24/36 [00:09<00:03,  3.43it/s]
J=1 E=10 D=4 predict1:  67%|██████▋   | 24/36 [00:09<00:03,  3.43it/s]
J=1 E=10 D=4 predictB:  67%|██████▋   | 24/36 [00:09<00:03,  3.43it/s]
J=1 E=10 D=4 predictO:  67%|██████▋   | 24/36 [00:09<00:03,  3.43it/s]
J=1 E=10 D=6 train rf:  67%|██████▋   | 24/36 [00:09<00:03,  3.43it/s]
J=1 E=10 D=6 ISession:  67%|██████▋   | 24/36 [00:09<00:03,  3.43it/s]
J=1 E=10 D=6 cvt onnx:  67%|██████▋   | 24/36 [00:09<00:03,  3.43it/s]
J=1 E=10 D=6 predict1:  67%|██████▋   | 24/36 [00:09<00:03,  3.43it/s]
J=1 E=10 D=6 predictB:  67%|██████▋   | 24/36 [00:09<00:03,  3.43it/s]
J=1 E=10 D=6 predictO:  67%|██████▋   | 24/36 [00:09<00:03,  3.43it/s]
J=1 E=10 D=6 predictO:  78%|███████▊  | 28/36 [00:09<00:00,  8.12it/s]
J=1 E=10 D=8 train rf:  78%|███████▊  | 28/36 [00:09<00:00,  8.12it/s]
J=1 E=10 D=8 ISession:  78%|███████▊  | 28/36 [00:09<00:00,  8.12it/s]
J=1 E=10 D=8 cvt onnx:  78%|███████▊  | 28/36 [00:09<00:00,  8.12it/s]
J=1 E=10 D=8 predict1:  78%|███████▊  | 28/36 [00:09<00:00,  8.12it/s]
J=1 E=10 D=8 predictB:  78%|███████▊  | 28/36 [00:09<00:00,  8.12it/s]
J=1 E=10 D=8 predictO:  78%|███████▊  | 28/36 [00:09<00:00,  8.12it/s]
J=1 E=10 D=10 train rf:  78%|███████▊  | 28/36 [00:09<00:00,  8.12it/s]
J=1 E=10 D=10 ISession:  78%|███████▊  | 28/36 [00:09<00:00,  8.12it/s]
J=1 E=10 D=10 cvt onnx:  78%|███████▊  | 28/36 [00:09<00:00,  8.12it/s]
J=1 E=10 D=10 predict1:  78%|███████▊  | 28/36 [00:09<00:00,  8.12it/s]
J=1 E=10 D=10 predictB:  78%|███████▊  | 28/36 [00:09<00:00,  8.12it/s]
J=1 E=10 D=10 predictO:  78%|███████▊  | 28/36 [00:09<00:00,  8.12it/s]
J=1 E=10 D=10 predictO:  94%|█████████▍| 34/36 [00:09<00:00, 14.98it/s]
J=1 E=10 D=10 predictO: 100%|██████████| 36/36 [00:09<00:00,  3.65it/s]

Saving data¶

name = os.path.join(cache_dir, "plot_beanchmark_rf")
print(f"Saving data into {name!r}")

df = pandas.DataFrame(data)
df2 = df.copy()
df2["legend"] = legend
df2.to_csv(f"{name}-{legend}.csv", index=False)

Saving data into '_cache/plot_beanchmark_rf'

Printing the data

df

	n_jobs	max_depth	n_estimators	repeat	max_time	name	n_rows	n_features	onnx_size	avg	med	n_runs	ttime
0	20	4	10	7	5	base	1000	10	11460	0.020402	0.019292	7	0.166615
1	20	4	10	7	5	ort_	1000	10	11460	0.000432	0.000438	7	0.003177
2	20	4	20	7	5	base	1000	10	22145	0.040205	0.042595	7	0.286761
3	20	4	20	7	5	ort_	1000	10	22145	0.000992	0.000726	7	0.008394
4	20	4	30	7	5	base	1000	10	32536	0.027468	0.028868	7	0.206444
5	20	4	30	7	5	ort_	1000	10	32536	0.000506	0.000365	7	0.004230
6	20	6	10	7	5	base	1000	10	34530	0.019679	0.017354	7	0.171011
7	20	6	10	7	5	ort_	1000	10	34530	0.000103	0.000074	7	0.001878
8	20	6	20	7	5	base	1000	10	66529	0.017820	0.017489	7	0.132340
9	20	6	20	7	5	ort_	1000	10	66529	0.000156	0.000139	7	0.001469
10	20	6	30	7	5	base	1000	10	103420	0.022106	0.021207	7	0.158302
11	20	6	30	7	5	ort_	1000	10	103420	0.000321	0.000330	7	0.003994
12	20	8	10	7	5	base	1000	10	71350	0.030077	0.026227	7	0.217749
13	20	8	10	7	5	ort_	1000	10	71350	0.000284	0.000135	7	0.002352
14	20	8	20	7	5	base	1000	10	144167	0.024029	0.021634	7	0.200874
15	20	8	20	7	5	ort_	1000	10	144167	0.000488	0.000375	7	0.004292
16	20	8	30	7	5	base	1000	10	214110	0.044221	0.039483	7	0.318789
17	20	8	30	7	5	ort_	1000	10	214110	0.000797	0.000472	7	0.006995
18	20	10	10	7	5	base	1000	10	122048	0.028782	0.031307	7	0.197500
19	20	10	10	7	5	ort_	1000	10	122048	0.000159	0.000143	7	0.001353
20	20	10	20	7	5	base	1000	10	219442	0.038451	0.034949	7	0.271147
21	20	10	20	7	5	ort_	1000	10	219442	0.000247	0.000232	7	0.007190
22	20	10	30	7	5	base	1000	10	334072	0.021335	0.019029	7	0.169890
23	20	10	30	7	5	ort_	1000	10	334072	0.000316	0.000321	7	0.002366
24	10	4	10	7	5	base	1000	10	11679	0.017994	0.017969	7	0.125971
25	10	4	10	7	5	ort_	1000	10	11679	0.000219	0.000226	7	0.001612
26	10	4	20	7	5	base	1000	10	22656	0.017507	0.017571	7	0.130793
27	10	4	20	7	5	ort_	1000	10	22656	0.000192	0.000177	7	0.001623
28	10	4	30	7	5	base	1000	10	33412	0.029199	0.029476	7	0.203991
29	10	4	30	7	5	ort_	1000	10	33412	0.000310	0.000248	7	0.002301
30	10	6	10	7	5	base	1000	10	33727	0.017788	0.017760	7	0.123793
31	10	6	10	7	5	ort_	1000	10	33727	0.000181	0.000092	7	0.001484
32	10	6	20	7	5	base	1000	10	66894	0.025162	0.029113	7	0.174407
33	10	6	20	7	5	ort_	1000	10	66894	0.000245	0.000235	7	0.001975
34	10	6	30	7	5	base	1000	10	101960	0.030069	0.029910	7	0.211250
35	10	6	30	7	5	ort_	1000	10	101960	0.000275	0.000248	7	0.002105
36	10	8	10	7	5	base	1000	10	73532	0.018503	0.018575	7	0.129667
37	10	8	10	7	5	ort_	1000	10	73532	0.000219	0.000179	7	0.001621
38	10	8	20	7	5	base	1000	10	149551	0.021080	0.019247	7	0.153584
39	10	8	20	7	5	ort_	1000	10	149551	0.000212	0.000211	7	0.001832
40	10	8	30	7	5	base	1000	10	222210	0.029159	0.029022	7	0.205343
41	10	8	30	7	5	ort_	1000	10	222210	0.000406	0.000397	7	0.003140
42	10	10	10	7	5	base	1000	10	114799	0.018103	0.017797	7	0.128269
43	10	10	10	7	5	ort_	1000	10	114799	0.000224	0.000153	7	0.002583
44	10	10	20	7	5	base	1000	10	227708	0.017079	0.017073	7	0.125737
45	10	10	20	7	5	ort_	1000	10	227708	0.000316	0.000296	7	0.002357
46	10	10	30	7	5	base	1000	10	338925	0.028174	0.027690	7	0.197377
47	10	10	30	7	5	ort_	1000	10	338925	0.000530	0.000529	7	0.004071
48	1	4	10	7	5	base	1000	10	11168	0.000785	0.000712	7	0.005677
49	1	4	10	7	5	ort_	1000	10	11168	0.000258	0.000268	7	0.001803
50	1	6	10	7	5	base	1000	10	33216	0.000832	0.000769	7	0.005944
51	1	6	10	7	5	ort_	1000	10	33216	0.000321	0.000313	7	0.002284
52	1	8	10	7	5	base	1000	10	77275	0.001040	0.001066	7	0.007312
53	1	8	10	7	5	ort_	1000	10	77275	0.000456	0.000448	7	0.003227
54	1	10	10	7	5	base	1000	10	117218	0.001015	0.001011	7	0.007275
55	1	10	10	7	5	ort_	1000	10	117218	0.000531	0.000523	7	0.003769

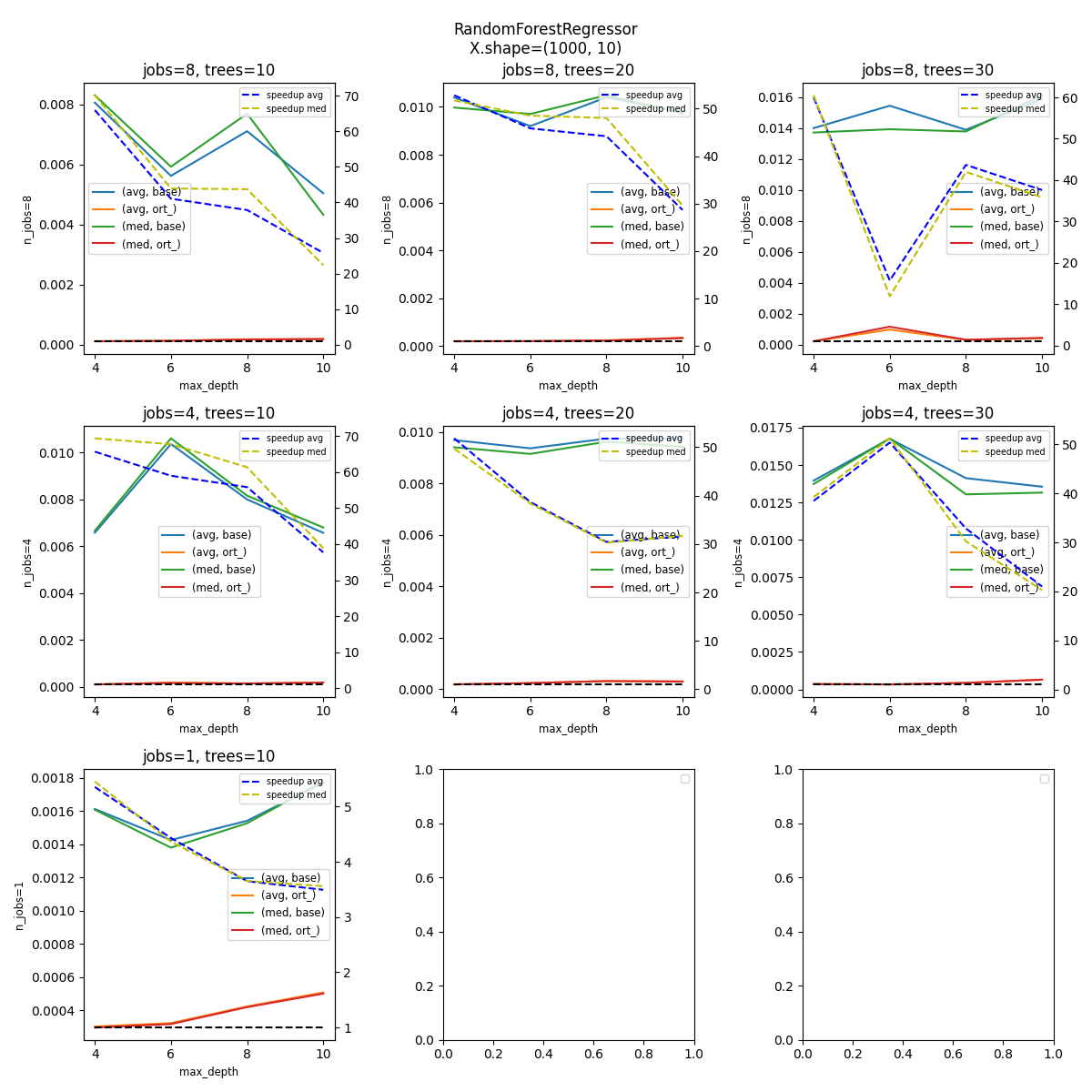
Plot¶

n_rows = len(n_jobs)
n_cols = len(n_ests)


fig, axes = plt.subplots(n_rows, n_cols, figsize=(4 * n_cols, 4 * n_rows))
fig.suptitle(f"{rf.__class__.__name__}\nX.shape={X.shape}")

for n_j, n_estimators in tqdm(product(n_jobs, n_ests)):
    i = n_jobs.index(n_j)
    j = n_ests.index(n_estimators)
    ax = axes[i, j]

    subdf = df[(df.n_estimators == n_estimators) & (df.n_jobs == n_j)]
    if subdf.shape[0] == 0:
        continue
    piv = subdf.pivot(index="max_depth", columns="name", values=["avg", "med"])
    piv.plot(ax=ax, title=f"jobs={n_j}, trees={n_estimators}")
    ax.set_ylabel(f"n_jobs={n_j}", fontsize="small")
    ax.set_xlabel("max_depth", fontsize="small")

    # ratio
    ax2 = ax.twinx()
    piv1 = subdf.pivot(index="max_depth", columns="name", values="avg")
    piv1["speedup"] = piv1.base / piv1.ort_
    ax2.plot(piv1.index, piv1.speedup, "b--", label="speedup avg")

    piv1 = subdf.pivot(index="max_depth", columns="name", values="med")
    piv1["speedup"] = piv1.base / piv1.ort_
    ax2.plot(piv1.index, piv1.speedup, "y--", label="speedup med")
    ax2.legend(fontsize="x-small")

    # 1
    ax2.plot(piv1.index, [1 for _ in piv1.index], "k--", label="no speedup")

for i in range(axes.shape[0]):
    for j in range(axes.shape[1]):
        axes[i, j].legend(fontsize="small")

fig.tight_layout()
fig.savefig(f"{name}-{legend}.png")
# plt.show()

RandomForestRegressor X.shape=(1000, 10), jobs=20, trees=10, jobs=20, trees=20, jobs=20, trees=30, jobs=10, trees=10, jobs=10, trees=20, jobs=10, trees=30, jobs=1, trees=10

0it [00:00, ?it/s]
4it [00:00, 38.92it/s]
8it [00:00, 32.62it/s]
9it [00:00, 37.54it/s]
~/github/onnx-array-api/_doc/examples/plot_benchmark_rf.py:307: UserWarning: No artists with labels found to put in legend.  Note that artists whose label start with an underscore are ignored when legend() is called with no argument.
  axes[i, j].legend(fontsize="small")

Total running time of the script: (0 minutes 13.510 seconds)

Gallery generated by Sphinx-Gallery