Benchmark of TreeEnsemble implementation#

The following example compares the inference time between onnxruntime and sklearn.ensemble.RandomForestRegressor, fow different number of estimators, max depth, and parallelization. It does it for a fixed number of rows and features.

import and registration of necessary converters#

import pickle
import os
import time
from itertools import product

import matplotlib.pyplot as plt
import numpy
import pandas
from lightgbm import LGBMRegressor
from onnxmltools.convert.lightgbm.operator_converters.LightGbm import convert_lightgbm
from onnxmltools.convert.xgboost.operator_converters.XGBoost import convert_xgboost
from onnxruntime import InferenceSession, SessionOptions
from psutil import cpu_count
from sphinx_runpython.runpython import run_cmd
from skl2onnx import to_onnx, update_registered_converter
from skl2onnx.common.shape_calculator import calculate_linear_regressor_output_shapes
from sklearn import set_config
from sklearn.ensemble import RandomForestRegressor
from tqdm import tqdm
from xgboost import XGBRegressor


def skl2onnx_convert_lightgbm(scope, operator, container):
    options = scope.get_options(operator.raw_operator)
    if "split" in options:
        operator.split = options["split"]
    else:
        operator.split = None
    convert_lightgbm(scope, operator, container)


update_registered_converter(
    LGBMRegressor,
    "LightGbmLGBMRegressor",
    calculate_linear_regressor_output_shapes,
    skl2onnx_convert_lightgbm,
    options={"split": None},
)
update_registered_converter(
    XGBRegressor,
    "XGBoostXGBRegressor",
    calculate_linear_regressor_output_shapes,
    convert_xgboost,
)

# The following instruction reduces the time spent by scikit-learn
# to validate the data.
set_config(assume_finite=True)

Machine details#

print(f"Number of cores: {cpu_count()}")

Number of cores: 8

But this information is not usually enough. Let’s extract the cache information.

try:
    out, err = run_cmd("lscpu")
    print(out)
except Exception as e:
    print(f"lscpu not available: {e}")

['lscpu']
<Popen: returncode: None args: ['lscpu']>

Or with the following command.

out, err = run_cmd("cat /proc/cpuinfo")
print(out)

['cat', '/proc/cpuinfo']
<Popen: returncode: None args: ['cat', '/proc/cpuinfo']>

Fonction to measure inference time#

def measure_inference(fct, X, repeat, max_time=5, quantile=1):
    """
    Run *repeat* times the same function on data *X*.

    :param fct: fonction to run
    :param X: data
    :param repeat: number of times to run
    :param max_time: maximum time to use to measure the inference
    :return: number of runs, sum of the time, average, median
    """
    times = []
    for n in range(repeat):
        perf = time.perf_counter()
        fct(X)
        delta = time.perf_counter() - perf
        times.append(delta)
        if len(times) < 3:
            continue
        if max_time is not None and sum(times) >= max_time:
            break
    times.sort()
    quantile = 0 if (len(times) - quantile * 2) < 3 else quantile
    if quantile == 0:
        tt = times
    else:
        tt = times[quantile:-quantile]
    return (len(times), sum(times), sum(tt) / len(tt), times[len(times) // 2])

Benchmark#

The following script benchmarks the inference for the same model for a random forest and onnxruntime after it was converted into ONNX and for the following configurations.

small = cpu_count() < 12
if small:
    N = 1000
    n_features = 10
    n_jobs = [1, cpu_count() // 2, cpu_count()]
    n_ests = [10, 20, 30]
    depth = [4, 6, 8, 10]
    Regressor = RandomForestRegressor
else:
    N = 100000
    n_features = 50
    n_jobs = [cpu_count(), cpu_count() // 2, 1]
    n_ests = [100, 200, 400]
    depth = [6, 8, 10, 12, 14]
    Regressor = RandomForestRegressor

legend = f"parallel-nf-{n_features}-"

# avoid duplicates on machine with 1 or 2 cores.
n_jobs = list(sorted(set(n_jobs), reverse=True))

Benchmark parameters

repeat = 7  # repeat n times the same inference
quantile = 1  # exclude extreme times
max_time = 5  # maximum number of seconds to spend on one configuration

Data

X = numpy.random.randn(N, n_features).astype(numpy.float32)
noise = (numpy.random.randn(X.shape[0]) / (n_features // 5)).astype(numpy.float32)
y = X.mean(axis=1) + noise
n_train = min(N, N // 3)


data = []
couples = list(product(n_jobs, depth, n_ests))
bar = tqdm(couples)
cache_dir = "_cache"
if not os.path.exists(cache_dir):
    os.mkdir(cache_dir)

for n_j, max_depth, n_estimators in bar:
    if n_j == 1 and n_estimators > n_ests[0]:
        # skipping
        continue

    # parallelization
    cache_name = os.path.join(
        cache_dir, f"nf-{X.shape[1]}-rf-J-{n_j}-E-{n_estimators}-D-{max_depth}.pkl"
    )
    if os.path.exists(cache_name):
        with open(cache_name, "rb") as f:
            rf = pickle.load(f)
    else:
        bar.set_description(f"J={n_j} E={n_estimators} D={max_depth} train rf")
        if n_j == 1 and issubclass(Regressor, RandomForestRegressor):
            rf = Regressor(max_depth=max_depth, n_estimators=n_estimators, n_jobs=-1)
            rf.fit(X[:n_train], y[:n_train])
            rf.n_jobs = 1
        else:
            rf = Regressor(max_depth=max_depth, n_estimators=n_estimators, n_jobs=n_j)
            rf.fit(X[:n_train], y[:n_train])
        with open(cache_name, "wb") as f:
            pickle.dump(rf, f)

    bar.set_description(f"J={n_j} E={n_estimators} D={max_depth} ISession")
    so = SessionOptions()
    so.intra_op_num_threads = n_j
    cache_name = os.path.join(
        cache_dir, f"nf-{X.shape[1]}-rf-J-{n_j}-E-{n_estimators}-D-{max_depth}.onnx"
    )
    if os.path.exists(cache_name):
        sess = InferenceSession(cache_name, so, providers=["CPUExecutionProvider"])
    else:
        bar.set_description(f"J={n_j} E={n_estimators} D={max_depth} cvt onnx")
        onx = to_onnx(rf, X[:1])
        with open(cache_name, "wb") as f:
            f.write(onx.SerializeToString())
        sess = InferenceSession(cache_name, so, providers=["CPUExecutionProvider"])
    onx_size = os.stat(cache_name).st_size

    # run once to avoid counting the first run
    bar.set_description(f"J={n_j} E={n_estimators} D={max_depth} predict1")
    rf.predict(X)
    sess.run(None, {"X": X})

    # fixed data
    obs = dict(
        n_jobs=n_j,
        max_depth=max_depth,
        n_estimators=n_estimators,
        repeat=repeat,
        max_time=max_time,
        name=rf.__class__.__name__,
        n_rows=X.shape[0],
        n_features=X.shape[1],
        onnx_size=onx_size,
    )

    # baseline
    bar.set_description(f"J={n_j} E={n_estimators} D={max_depth} predictB")
    r, t, mean, med = measure_inference(rf.predict, X, repeat=repeat, max_time=max_time)
    o1 = obs.copy()
    o1.update(dict(avg=mean, med=med, n_runs=r, ttime=t, name="base"))
    data.append(o1)

    # onnxruntime
    bar.set_description(f"J={n_j} E={n_estimators} D={max_depth} predictO")
    r, t, mean, med = measure_inference(
        lambda x: sess.run(None, {"X": x}), X, repeat=repeat, max_time=max_time
    )
    o2 = obs.copy()
    o2.update(dict(avg=mean, med=med, n_runs=r, ttime=t, name="ort_"))
    data.append(o2)

  0%|          | 0/36 [00:00<?, ?it/s]
J=8 E=10 D=4 ISession:   0%|          | 0/36 [00:00<?, ?it/s]
J=8 E=10 D=4 predict1:   0%|          | 0/36 [00:00<?, ?it/s]
J=8 E=10 D=4 predictB:   0%|          | 0/36 [00:00<?, ?it/s]
J=8 E=10 D=4 predictO:   0%|          | 0/36 [00:00<?, ?it/s]
J=8 E=10 D=4 predictO:   3%|2         | 1/36 [00:00<00:04,  8.48it/s]
J=8 E=20 D=4 ISession:   3%|2         | 1/36 [00:00<00:04,  8.48it/s]
J=8 E=20 D=4 predict1:   3%|2         | 1/36 [00:00<00:04,  8.48it/s]
J=8 E=20 D=4 predictB:   3%|2         | 1/36 [00:00<00:04,  8.48it/s]
J=8 E=20 D=4 predictO:   3%|2         | 1/36 [00:00<00:04,  8.48it/s]
J=8 E=20 D=4 predictO:   6%|5         | 2/36 [00:00<00:04,  7.28it/s]
J=8 E=30 D=4 ISession:   6%|5         | 2/36 [00:00<00:04,  7.28it/s]
J=8 E=30 D=4 predict1:   6%|5         | 2/36 [00:00<00:04,  7.28it/s]
J=8 E=30 D=4 predictB:   6%|5         | 2/36 [00:00<00:04,  7.28it/s]
J=8 E=30 D=4 predictO:   6%|5         | 2/36 [00:00<00:04,  7.28it/s]
J=8 E=30 D=4 predictO:   8%|8         | 3/36 [00:00<00:05,  6.03it/s]
J=8 E=10 D=6 ISession:   8%|8         | 3/36 [00:00<00:05,  6.03it/s]
J=8 E=10 D=6 predict1:   8%|8         | 3/36 [00:00<00:05,  6.03it/s]
J=8 E=10 D=6 predictB:   8%|8         | 3/36 [00:00<00:05,  6.03it/s]
J=8 E=10 D=6 predictO:   8%|8         | 3/36 [00:00<00:05,  6.03it/s]
J=8 E=10 D=6 predictO:  11%|#1        | 4/36 [00:00<00:04,  7.04it/s]
J=8 E=20 D=6 ISession:  11%|#1        | 4/36 [00:00<00:04,  7.04it/s]
J=8 E=20 D=6 predict1:  11%|#1        | 4/36 [00:00<00:04,  7.04it/s]
J=8 E=20 D=6 predictB:  11%|#1        | 4/36 [00:00<00:04,  7.04it/s]
J=8 E=20 D=6 predictO:  11%|#1        | 4/36 [00:00<00:04,  7.04it/s]
J=8 E=20 D=6 predictO:  14%|#3        | 5/36 [00:00<00:04,  7.07it/s]
J=8 E=30 D=6 ISession:  14%|#3        | 5/36 [00:00<00:04,  7.07it/s]
J=8 E=30 D=6 predict1:  14%|#3        | 5/36 [00:00<00:04,  7.07it/s]
J=8 E=30 D=6 predictB:  14%|#3        | 5/36 [00:00<00:04,  7.07it/s]
J=8 E=30 D=6 predictO:  14%|#3        | 5/36 [00:00<00:04,  7.07it/s]
J=8 E=30 D=6 predictO:  17%|#6        | 6/36 [00:00<00:04,  6.53it/s]
J=8 E=10 D=8 ISession:  17%|#6        | 6/36 [00:00<00:04,  6.53it/s]
J=8 E=10 D=8 predict1:  17%|#6        | 6/36 [00:00<00:04,  6.53it/s]
J=8 E=10 D=8 predictB:  17%|#6        | 6/36 [00:00<00:04,  6.53it/s]
J=8 E=10 D=8 predictO:  17%|#6        | 6/36 [00:01<00:04,  6.53it/s]
J=8 E=10 D=8 predictO:  19%|#9        | 7/36 [00:01<00:04,  7.16it/s]
J=8 E=20 D=8 ISession:  19%|#9        | 7/36 [00:01<00:04,  7.16it/s]
J=8 E=20 D=8 predict1:  19%|#9        | 7/36 [00:01<00:04,  7.16it/s]
J=8 E=20 D=8 predictB:  19%|#9        | 7/36 [00:01<00:04,  7.16it/s]
J=8 E=20 D=8 predictO:  19%|#9        | 7/36 [00:01<00:04,  7.16it/s]
J=8 E=20 D=8 predictO:  22%|##2       | 8/36 [00:01<00:04,  6.98it/s]
J=8 E=30 D=8 ISession:  22%|##2       | 8/36 [00:01<00:04,  6.98it/s]
J=8 E=30 D=8 predict1:  22%|##2       | 8/36 [00:01<00:04,  6.98it/s]
J=8 E=30 D=8 predictB:  22%|##2       | 8/36 [00:01<00:04,  6.98it/s]
J=8 E=30 D=8 predictO:  22%|##2       | 8/36 [00:01<00:04,  6.98it/s]
J=8 E=30 D=8 predictO:  25%|##5       | 9/36 [00:01<00:04,  6.09it/s]
J=8 E=10 D=10 ISession:  25%|##5       | 9/36 [00:01<00:04,  6.09it/s]
J=8 E=10 D=10 predict1:  25%|##5       | 9/36 [00:01<00:04,  6.09it/s]
J=8 E=10 D=10 predictB:  25%|##5       | 9/36 [00:01<00:04,  6.09it/s]
J=8 E=10 D=10 predictO:  25%|##5       | 9/36 [00:01<00:04,  6.09it/s]
J=8 E=10 D=10 predictO:  28%|##7       | 10/36 [00:01<00:03,  6.58it/s]
J=8 E=20 D=10 ISession:  28%|##7       | 10/36 [00:01<00:03,  6.58it/s]
J=8 E=20 D=10 predict1:  28%|##7       | 10/36 [00:01<00:03,  6.58it/s]
J=8 E=20 D=10 predictB:  28%|##7       | 10/36 [00:01<00:03,  6.58it/s]
J=8 E=20 D=10 predictO:  28%|##7       | 10/36 [00:01<00:03,  6.58it/s]
J=8 E=20 D=10 predictO:  31%|###       | 11/36 [00:01<00:03,  6.55it/s]
J=8 E=30 D=10 ISession:  31%|###       | 11/36 [00:01<00:03,  6.55it/s]
J=8 E=30 D=10 predict1:  31%|###       | 11/36 [00:01<00:03,  6.55it/s]
J=8 E=30 D=10 predictB:  31%|###       | 11/36 [00:01<00:03,  6.55it/s]
J=8 E=30 D=10 predictO:  31%|###       | 11/36 [00:01<00:03,  6.55it/s]
J=8 E=30 D=10 predictO:  33%|###3      | 12/36 [00:01<00:04,  5.84it/s]
J=4 E=10 D=4 ISession:  33%|###3      | 12/36 [00:01<00:04,  5.84it/s]
J=4 E=10 D=4 predict1:  33%|###3      | 12/36 [00:01<00:04,  5.84it/s]
J=4 E=10 D=4 predictB:  33%|###3      | 12/36 [00:01<00:04,  5.84it/s]
J=4 E=10 D=4 predictO:  33%|###3      | 12/36 [00:01<00:04,  5.84it/s]
J=4 E=20 D=4 ISession:  33%|###3      | 12/36 [00:01<00:04,  5.84it/s]
J=4 E=20 D=4 predict1:  33%|###3      | 12/36 [00:01<00:04,  5.84it/s]
J=4 E=20 D=4 predictB:  33%|###3      | 12/36 [00:01<00:04,  5.84it/s]
J=4 E=20 D=4 predictO:  33%|###3      | 12/36 [00:02<00:04,  5.84it/s]
J=4 E=20 D=4 predictO:  39%|###8      | 14/36 [00:02<00:03,  7.28it/s]
J=4 E=30 D=4 ISession:  39%|###8      | 14/36 [00:02<00:03,  7.28it/s]
J=4 E=30 D=4 predict1:  39%|###8      | 14/36 [00:02<00:03,  7.28it/s]
J=4 E=30 D=4 predictB:  39%|###8      | 14/36 [00:02<00:03,  7.28it/s]
J=4 E=30 D=4 predictO:  39%|###8      | 14/36 [00:02<00:03,  7.28it/s]
J=4 E=30 D=4 predictO:  42%|####1     | 15/36 [00:02<00:02,  7.14it/s]
J=4 E=10 D=6 ISession:  42%|####1     | 15/36 [00:02<00:02,  7.14it/s]
J=4 E=10 D=6 predict1:  42%|####1     | 15/36 [00:02<00:02,  7.14it/s]
J=4 E=10 D=6 predictB:  42%|####1     | 15/36 [00:02<00:02,  7.14it/s]
J=4 E=10 D=6 predictO:  42%|####1     | 15/36 [00:02<00:02,  7.14it/s]
J=4 E=20 D=6 ISession:  42%|####1     | 15/36 [00:02<00:02,  7.14it/s]
J=4 E=20 D=6 predict1:  42%|####1     | 15/36 [00:02<00:02,  7.14it/s]
J=4 E=20 D=6 predictB:  42%|####1     | 15/36 [00:02<00:02,  7.14it/s]
J=4 E=20 D=6 predictO:  42%|####1     | 15/36 [00:02<00:02,  7.14it/s]
J=4 E=20 D=6 predictO:  47%|####7     | 17/36 [00:02<00:02,  8.33it/s]
J=4 E=30 D=6 ISession:  47%|####7     | 17/36 [00:02<00:02,  8.33it/s]
J=4 E=30 D=6 predict1:  47%|####7     | 17/36 [00:02<00:02,  8.33it/s]
J=4 E=30 D=6 predictB:  47%|####7     | 17/36 [00:02<00:02,  8.33it/s]
J=4 E=30 D=6 predictO:  47%|####7     | 17/36 [00:02<00:02,  8.33it/s]
J=4 E=30 D=6 predictO:  50%|#####     | 18/36 [00:02<00:02,  7.79it/s]
J=4 E=10 D=8 ISession:  50%|#####     | 18/36 [00:02<00:02,  7.79it/s]
J=4 E=10 D=8 predict1:  50%|#####     | 18/36 [00:02<00:02,  7.79it/s]
J=4 E=10 D=8 predictB:  50%|#####     | 18/36 [00:02<00:02,  7.79it/s]
J=4 E=10 D=8 predictO:  50%|#####     | 18/36 [00:02<00:02,  7.79it/s]
J=4 E=20 D=8 ISession:  50%|#####     | 18/36 [00:02<00:02,  7.79it/s]
J=4 E=20 D=8 predict1:  50%|#####     | 18/36 [00:02<00:02,  7.79it/s]
J=4 E=20 D=8 predictB:  50%|#####     | 18/36 [00:02<00:02,  7.79it/s]
J=4 E=20 D=8 predictO:  50%|#####     | 18/36 [00:02<00:02,  7.79it/s]
J=4 E=20 D=8 predictO:  56%|#####5    | 20/36 [00:02<00:01,  8.63it/s]
J=4 E=30 D=8 ISession:  56%|#####5    | 20/36 [00:02<00:01,  8.63it/s]
J=4 E=30 D=8 predict1:  56%|#####5    | 20/36 [00:02<00:01,  8.63it/s]
J=4 E=30 D=8 predictB:  56%|#####5    | 20/36 [00:02<00:01,  8.63it/s]
J=4 E=30 D=8 predictO:  56%|#####5    | 20/36 [00:02<00:01,  8.63it/s]
J=4 E=30 D=8 predictO:  58%|#####8    | 21/36 [00:02<00:01,  8.29it/s]
J=4 E=10 D=10 ISession:  58%|#####8    | 21/36 [00:02<00:01,  8.29it/s]
J=4 E=10 D=10 predict1:  58%|#####8    | 21/36 [00:02<00:01,  8.29it/s]
J=4 E=10 D=10 predictB:  58%|#####8    | 21/36 [00:02<00:01,  8.29it/s]
J=4 E=10 D=10 predictO:  58%|#####8    | 21/36 [00:02<00:01,  8.29it/s]
J=4 E=20 D=10 ISession:  58%|#####8    | 21/36 [00:02<00:01,  8.29it/s]
J=4 E=20 D=10 predict1:  58%|#####8    | 21/36 [00:02<00:01,  8.29it/s]
J=4 E=20 D=10 predictB:  58%|#####8    | 21/36 [00:02<00:01,  8.29it/s]
J=4 E=20 D=10 predictO:  58%|#####8    | 21/36 [00:03<00:01,  8.29it/s]
J=4 E=20 D=10 predictO:  64%|######3   | 23/36 [00:03<00:01,  8.75it/s]
J=4 E=30 D=10 ISession:  64%|######3   | 23/36 [00:03<00:01,  8.75it/s]
J=4 E=30 D=10 predict1:  64%|######3   | 23/36 [00:03<00:01,  8.75it/s]
J=4 E=30 D=10 predictB:  64%|######3   | 23/36 [00:03<00:01,  8.75it/s]
J=4 E=30 D=10 predictO:  64%|######3   | 23/36 [00:03<00:01,  8.75it/s]
J=4 E=30 D=10 predictO:  67%|######6   | 24/36 [00:03<00:01,  7.32it/s]
J=1 E=10 D=4 ISession:  67%|######6   | 24/36 [00:03<00:01,  7.32it/s]
J=1 E=10 D=4 predict1:  67%|######6   | 24/36 [00:03<00:01,  7.32it/s]
J=1 E=10 D=4 predictB:  67%|######6   | 24/36 [00:03<00:01,  7.32it/s]
J=1 E=10 D=4 predictO:  67%|######6   | 24/36 [00:03<00:01,  7.32it/s]
J=1 E=10 D=6 ISession:  67%|######6   | 24/36 [00:03<00:01,  7.32it/s]
J=1 E=10 D=6 predict1:  67%|######6   | 24/36 [00:03<00:01,  7.32it/s]
J=1 E=10 D=6 predictB:  67%|######6   | 24/36 [00:03<00:01,  7.32it/s]
J=1 E=10 D=6 predictO:  67%|######6   | 24/36 [00:03<00:01,  7.32it/s]
J=1 E=10 D=8 ISession:  67%|######6   | 24/36 [00:03<00:01,  7.32it/s]
J=1 E=10 D=8 predict1:  67%|######6   | 24/36 [00:03<00:01,  7.32it/s]
J=1 E=10 D=8 predictB:  67%|######6   | 24/36 [00:03<00:01,  7.32it/s]
J=1 E=10 D=8 predictO:  67%|######6   | 24/36 [00:03<00:01,  7.32it/s]
J=1 E=10 D=10 ISession:  67%|######6   | 24/36 [00:03<00:01,  7.32it/s]
J=1 E=10 D=10 predict1:  67%|######6   | 24/36 [00:03<00:01,  7.32it/s]
J=1 E=10 D=10 predictB:  67%|######6   | 24/36 [00:03<00:01,  7.32it/s]
J=1 E=10 D=10 predictO:  67%|######6   | 24/36 [00:03<00:01,  7.32it/s]
J=1 E=10 D=10 predictO:  94%|#########4| 34/36 [00:03<00:00, 23.42it/s]
J=1 E=10 D=10 predictO: 100%|##########| 36/36 [00:03<00:00, 10.52it/s]

Saving data#

name = os.path.join(cache_dir, "plot_beanchmark_rf")
print(f"Saving data into {name!r}")

df = pandas.DataFrame(data)
df2 = df.copy()
df2["legend"] = legend
df2.to_csv(f"{name}-{legend}.csv", index=False)

Saving data into '_cache/plot_beanchmark_rf'

Printing the data

df

	n_jobs	max_depth	n_estimators	repeat	max_time	name	n_rows	n_features	onnx_size	avg	med	n_runs	ttime
0	8	4	10	7	5	base	1000	10	11089	0.013271	0.013449	7	0.090108
1	8	4	10	7	5	ort_	1000	10	11089	0.000161	0.000148	7	0.001510
2	8	4	20	7	5	base	1000	10	21920	0.012371	0.012129	7	0.109870
3	8	4	20	7	5	ort_	1000	10	21920	0.000163	0.000162	7	0.001428
4	8	4	30	7	5	base	1000	10	32822	0.019804	0.019161	7	0.141788
5	8	4	30	7	5	ort_	1000	10	32822	0.000877	0.000590	7	0.013612
6	8	6	10	7	5	base	1000	10	34816	0.008833	0.008909	7	0.064498
7	8	6	10	7	5	ort_	1000	10	34816	0.000176	0.000172	7	0.009211
8	8	6	20	7	5	base	1000	10	68349	0.012703	0.012669	7	0.090856
9	8	6	20	7	5	ort_	1000	10	68349	0.000267	0.000248	7	0.008172
10	8	6	30	7	5	base	1000	10	102465	0.016200	0.016205	7	0.112334
11	8	6	30	7	5	ort_	1000	10	102465	0.000350	0.000334	7	0.002725
12	8	8	10	7	5	base	1000	10	72981	0.008978	0.008909	7	0.064398
13	8	8	10	7	5	ort_	1000	10	72981	0.000190	0.000184	7	0.001647
14	8	8	20	7	5	base	1000	10	143302	0.014107	0.014066	7	0.103939
15	8	8	20	7	5	ort_	1000	10	143302	0.000301	0.000294	7	0.002321
16	8	8	30	7	5	base	1000	10	214018	0.017487	0.017749	7	0.123962
17	8	8	30	7	5	ort_	1000	10	214018	0.000425	0.000421	7	0.003134
18	8	10	10	7	5	base	1000	10	114952	0.009929	0.009477	7	0.074473
19	8	10	10	7	5	ort_	1000	10	114952	0.000218	0.000221	7	0.001768
20	8	10	20	7	5	base	1000	10	226847	0.013402	0.013138	7	0.092491
21	8	10	20	7	5	ort_	1000	10	226847	0.000377	0.000368	7	0.002925
22	8	10	30	7	5	base	1000	10	335254	0.016574	0.017075	7	0.116400
23	8	10	30	7	5	ort_	1000	10	335254	0.000426	0.000389	7	0.022789
24	4	4	10	7	5	base	1000	10	11673	0.008325	0.008347	7	0.058635
25	4	4	10	7	5	ort_	1000	10	11673	0.000169	0.000161	7	0.001344
26	4	4	20	7	5	base	1000	10	22212	0.013365	0.013688	7	0.093536
27	4	4	20	7	5	ort_	1000	10	22212	0.000228	0.000219	7	0.001773
28	4	4	30	7	5	base	1000	10	32749	0.016798	0.016740	7	0.117199
29	4	4	30	7	5	ort_	1000	10	32749	0.000335	0.000328	7	0.002524
30	4	6	10	7	5	base	1000	10	30290	0.007367	0.007323	7	0.052338
31	4	6	10	7	5	ort_	1000	10	30290	0.000188	0.000179	7	0.001521
32	4	6	20	7	5	base	1000	10	67619	0.012100	0.012238	7	0.084379
33	4	6	20	7	5	ort_	1000	10	67619	0.000298	0.000294	7	0.002286
34	4	6	30	7	5	base	1000	10	101516	0.017729	0.016861	7	0.125102
35	4	6	30	7	5	ort_	1000	10	101516	0.000431	0.000431	7	0.003188
36	4	8	10	7	5	base	1000	10	71504	0.008022	0.007967	7	0.056057
37	4	8	10	7	5	ort_	1000	10	71504	0.000186	0.000195	7	0.001497
38	4	8	20	7	5	base	1000	10	144705	0.011905	0.011980	7	0.082227
39	4	8	20	7	5	ort_	1000	10	144705	0.000403	0.000405	7	0.002959
40	4	8	30	7	5	base	1000	10	219945	0.014526	0.014843	7	0.101083
41	4	8	30	7	5	ort_	1000	10	219945	0.000421	0.000416	7	0.003187
42	4	10	10	7	5	base	1000	10	107465	0.007807	0.008008	7	0.054330
43	4	10	10	7	5	ort_	1000	10	107465	0.000289	0.000283	7	0.002224
44	4	10	20	7	5	base	1000	10	221779	0.012670	0.012907	7	0.088462
45	4	10	20	7	5	ort_	1000	10	221779	0.000445	0.000435	7	0.003255
46	4	10	30	7	5	base	1000	10	331281	0.016064	0.015825	7	0.118449
47	4	10	30	7	5	ort_	1000	10	331281	0.001272	0.000856	7	0.022613
48	1	4	10	7	5	base	1000	10	11600	0.001937	0.002212	7	0.013395
49	1	4	10	7	5	ort_	1000	10	11600	0.000523	0.000533	7	0.004870
50	1	6	10	7	5	base	1000	10	34159	0.001861	0.001879	7	0.013240
51	1	6	10	7	5	ort_	1000	10	34159	0.000431	0.000419	7	0.003082
52	1	8	10	7	5	base	1000	10	70489	0.001608	0.001600	7	0.011164
53	1	8	10	7	5	ort_	1000	10	70489	0.000464	0.000464	7	0.003275
54	1	10	10	7	5	base	1000	10	110428	0.001576	0.001558	7	0.011071
55	1	10	10	7	5	ort_	1000	10	110428	0.000532	0.000524	7	0.003770

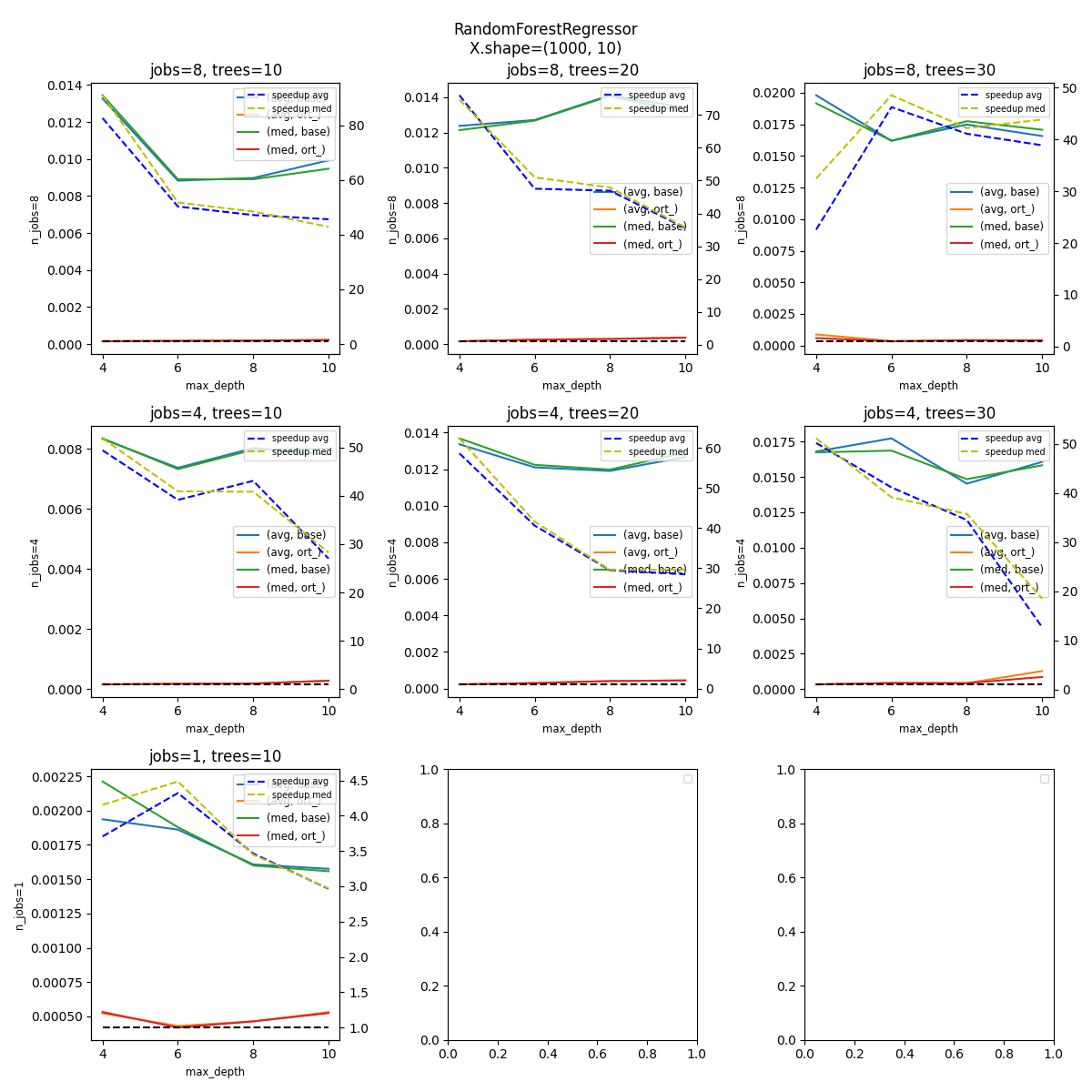
Plot#

n_rows = len(n_jobs)
n_cols = len(n_ests)


fig, axes = plt.subplots(n_rows, n_cols, figsize=(4 * n_cols, 4 * n_rows))
fig.suptitle(f"{rf.__class__.__name__}\nX.shape={X.shape}")

for n_j, n_estimators in tqdm(product(n_jobs, n_ests)):
    i = n_jobs.index(n_j)
    j = n_ests.index(n_estimators)
    ax = axes[i, j]

    subdf = df[(df.n_estimators == n_estimators) & (df.n_jobs == n_j)]
    if subdf.shape[0] == 0:
        continue
    piv = subdf.pivot(index="max_depth", columns="name", values=["avg", "med"])
    piv.plot(ax=ax, title=f"jobs={n_j}, trees={n_estimators}")
    ax.set_ylabel(f"n_jobs={n_j}", fontsize="small")
    ax.set_xlabel("max_depth", fontsize="small")

    # ratio
    ax2 = ax.twinx()
    piv1 = subdf.pivot(index="max_depth", columns="name", values="avg")
    piv1["speedup"] = piv1.base / piv1.ort_
    ax2.plot(piv1.index, piv1.speedup, "b--", label="speedup avg")

    piv1 = subdf.pivot(index="max_depth", columns="name", values="med")
    piv1["speedup"] = piv1.base / piv1.ort_
    ax2.plot(piv1.index, piv1.speedup, "y--", label="speedup med")
    ax2.legend(fontsize="x-small")

    # 1
    ax2.plot(piv1.index, [1 for _ in piv1.index], "k--", label="no speedup")

for i in range(axes.shape[0]):
    for j in range(axes.shape[1]):
        axes[i, j].legend(fontsize="small")

fig.tight_layout()
fig.savefig(f"{name}-{legend}.png")
# plt.show()

RandomForestRegressor X.shape=(1000, 10), jobs=8, trees=10, jobs=8, trees=20, jobs=8, trees=30, jobs=4, trees=10, jobs=4, trees=20, jobs=4, trees=30, jobs=1, trees=10

0it [00:00, ?it/s]
2it [00:00, 16.56it/s]
5it [00:00, 18.71it/s]
7it [00:00, 19.10it/s]
9it [00:00, 24.01it/s]

Total running time of the script: ( 0 minutes 7.878 seconds)

Gallery generated by Sphinx-Gallery